蚁群算法在非圆弧滑动面边坡稳定分析中的应用

蒋 莉，郭 强，刘宪亮

（1.华北水利水电学院，河南 郑州 450011；2.中水北方勘测设计研究有限责任公司，天津 河西 300222；3.黄河水利职业技术学院，河南 开封 475004）

0 引言

在边坡稳定分析中，如果目标函数为凸函数，且搜索空间比较规则，应用传统的分析方法容易得到最优解。 但复杂条件下的边坡稳定性分析是一个含多极值点、目标函数无确切表达式的非线性规划问题，对这种问题，再用传统的优化方法就难以搜索到全局最优解(最危险滑动面)。 蚁群算法(Ant Colony Algorithm)是意大利学者Marco. Dorigo 等人在自然界蚁群集体行为特征的启发下提出来的一种新型仿生算法。 该算法对目标函数无特殊要求，适用于目标函数为高度非线性、非凸或离散型的最优化模型。本文试运用蚁群算法，并结合斯宾塞（Spencer）法，对非均质边坡进行稳定分析，通过对非圆弧滑动面的搜索，确定最危险滑动面位置及其对应的最小安全系数。

1 蚁群算法简介

1.1 蚁群算法的思想起源[1]

自然界中，蚂蚁、蜜蜂、飞蛾等群居昆虫个体行为极其简单，但由多个个体组成的群体却呈现出有规律的行为。 蚂蚁在搜索食物源并搬运食物回巢穴时，其个体之间通过一种称之为信息素(Pheromone)的化学物质进行信息传递。 每只蚂蚁能够在它所经过的路径上释放、感知这种化学物质，并能够根据该化学物质的强弱决定自己的运动方向。 由此蚁群的集体行为就表现出一种信息正反馈现象：某一路径上走过的蚂蚁数越多，留下的信息素痕迹(Trail)就越多，后来蚂蚁选择该路径的概率也就越大。 蚂蚁群体正是通过这种行为最终找到通往目的地的最佳路径的。

1.2 蚁群算法的优点

受蚁群这种集体行为启发而提出的蚁群算法是基于种群进化的算法，易于实现分布式并行计算，且具有灵活性和开放性，可通过移植、杂交等方法同其他算法相结合，以改善算法的性能，或形成新的算法。它通过对目标函数的自适应来调整蚂蚁的搜索行为， 并通过路径选择过程中的多样性来保证得到更多的搜索空间，能够对多变量、非线性的复杂问题进行优化，并快速地得到全局最优解。 蚁群算法首先应用于求解TSP 问题(Traveling Salesman Problem，旅行商问题)，并取得了较好的效果。 由于具有较强的鲁棒性，对蚁群系统模型稍加修改，便可用来求解其他类型的规划或决策问题。

1.3 应用蚁群算法应遵循的规则

蚁群算法在完成整个任务的过程应遵循如下规则：（1）蚂蚁观察到的范围为一个方格形状，并且移动的距离也在此范围内，每只蚂蚁仅能感知其范围内的环境信息。 （2）蚂蚁在可感知的范围内觅食或寻蚁穴，如果存在目标，直接过去，否则，看是否有信息素，并朝信息素浓的方向前进。 （3）每只蚂蚁都朝信息素最浓的方向移动，如果周围没有信息素诱导，蚂蚁将按照自己的原运动方向前进。（4）若蚂蚁的移动方向被障碍物遮挡，它会随机地选择其他方向;如果有信息素指引，它将朝信息素浓的方向前进。 （5）每只蚂蚁在刚找到食物或者蚁穴时散发的信息素最多，随着所走距离的增加，信息素以一定速率在环境中挥发。

2 蚁群算法对非圆弧滑动面的搜索

2.1 基本思路

工程上对非圆弧临界滑动面安全系数的求解主要有简布法、摩根斯坦一普赖斯法以及沙尔玛法等。 斯宾塞法是摩根斯坦一普赖斯法的一个特例，它假定土条侧向力为常数，在很多情况下，采用该法所得的安全系数满足工程要求[2]。 本文使用斯宾塞法计算边坡的安全系数，其计算公式和计算方法可参见文献[2]。

由于临界滑动面所对应的安全系数是所有可能滑动面对应安全系数的最小值，因此，可将在边坡稳定中搜索临界滑动面的问题视为蚂蚁搜寻最佳路径的问题。 采用蚁群算法搜索非圆弧滑动面边坡的临界滑动面的步骤为：（1）划分网格，使边坡体离散（如图1 所示），并将入口区和出口区坡面上的各点分别引向虚拟点START 点和END 点。 滑体入口点至START 点和逸出点至END 点只作引导蚂蚁搜索滑动面用，不参与边坡安全系数计算。 （2）设置一定数量的人工蚂蚁，每只蚂蚁从START 点出发，随机地向END 点移动。人工蚂蚁在网格顶点间爬行的路径即可视为边坡的任一滑动面。 （3）计算每只蚂蚁走过路径的安全系数值。 该值与蚂蚁在路径上留下的信息素强度有关。 由于每只蚂蚁在它所经过的路径上留下了不同数量的痕迹，因此，每次循环后，蚂蚁选择路径的概率都会改变。 对于最佳路径，即安全系数最小的滑动面，留在其上的信息素量会越来越大， 蚂蚁选择这条路径的概率也会越来越大，最终所有的蚂蚁都会选择这条路径。

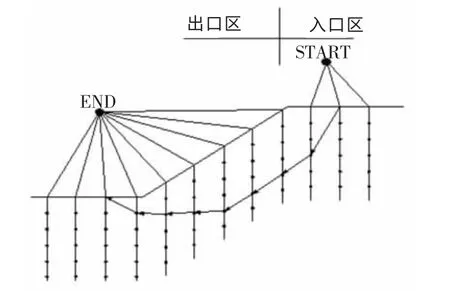
图1 边坡体离散及滑动面搜索Fig.1 Slope discrete and search for slip surface

2.2 数学模型

边坡稳定分析中，目标函数是Min(Fs)，即寻找令Fs最小的路径。 根据路径上信息素强度的不同，蚂蚁以不同的概率选择路径，最终找到令目标函数成立的路径。而蚂蚁只能在一定范围内移动，如图1中的一些结点即为蚂蚁可以移动的范围。 这个范围就是问题的约束条件，而这些点的密集程度影响着所求解的精确。

为解决满足工程实际问题的需要，应构建如图2 所示的多阶段不完全序贯决策问题。 由图2 可能看出，在起点B 与终点E 之间有N 层结点，它们将问题分成N+1 个阶段。 在问题的决策过程中，从起点B 始，在入口区根据决策准则进入第u 层的第一个结点(u，1)(u∈{1,2,…,q})，然后按顺序逐层决策，至出口区第v 层的第一个结点(v，1)v∈{q,q+1, …,N}，最后到达终点E。

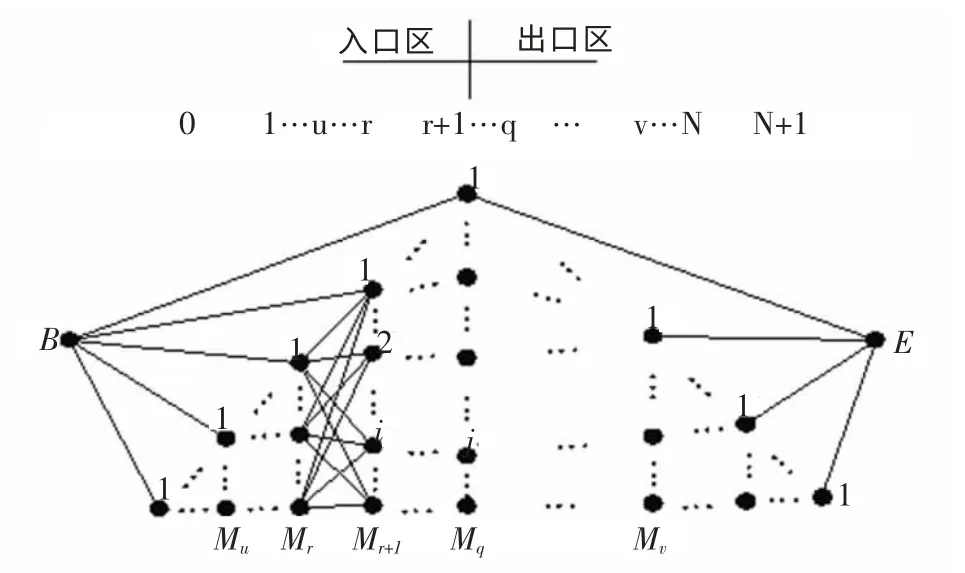
图2 多阶段不完全序贯决策问题Fig.2 Multistage incomplete sequence decision-making problem

根据蚁群算法基本原理，假设(r，i)表示第r 层中的第i 个节点，(r＋1，j)表示第r+1 层中的第j 个结点。[(r，i)，(r＋1，j)]表示结点(r，i)到结点(r＋1，j)的连线，则t 时刻蚂蚁k 由起点B 转移至结点(u，1)，或者由结点(r，i)转移到结点(r＋1，j)的转移概率可表示为

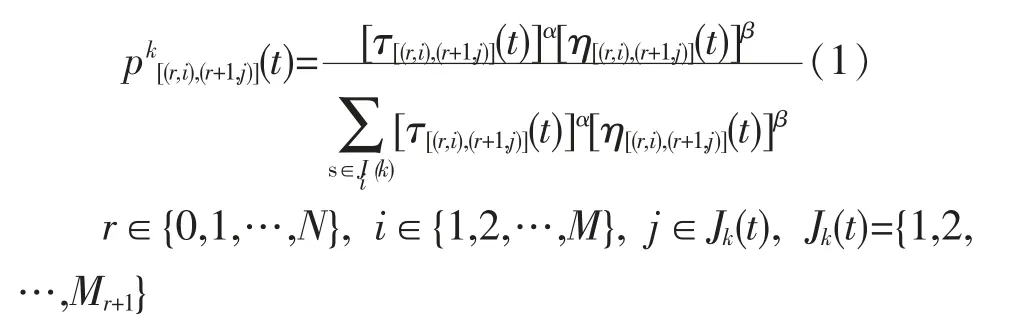
式中： τ[(r,i),(r+1,j)](t)为时刻t 在节点(r，i)、(r＋1，j)连线上残留的信息素痕迹强度(Intensity),初始时各条路径上信息素痕迹强度相等,即τij(t)=0(或设定等于某个常数C)；η[(r,i),(r+1,j)](t)为时刻t 在节点(r，i)、(r＋1,j)连线上的信息素痕迹能见度(Visibility)，且η[(r,i),(r+1,j)](t)=1/d[(r,i),(r+1,j)](t),d[(r,i),(r+1,j)]为点(r，i)至(r＋1，j)的距离；α、β 分别表示信息素痕迹强度和能见度在蚂蚁选择路径时的相对重要程度指数(α≥0、β≥0)；Ji(k)为处在位置i 的蚂蚁k 下一步允许选择的区位集合。

由于人工蚁群系统具有一定的记忆功能，它们能记住已走过的城市，若用tabuk(k=1,2,…,m)记录蚂蚁k 目前已走过的区位，则有Ji(k)={0,1,…,n}-tabuk。式（1）中的关键是如何确定残留在路径上的信息素强度τ[(r,i),(r+1,j)]和调整项η[(r,i),(r+1,j)]。 对于η[(r,i),(r+1,j)]，本文采用均匀分布法,即蚂蚁由条分线r 转移到条分线(r＋1)时，条分线上的每点被选中的概率相等。 此时

人工蚁群保留了自然蚁群信息素挥发的特点，随着时间的推移，以前留下的信息素逐渐消逝。 参数ρ(0≤ρ＜1)表示信息素的持久性， 1-ρ 则表示信息素的衰减度。 τ[(r,i),(r+1,j)](t)经过一次循环后按式（3）调整。

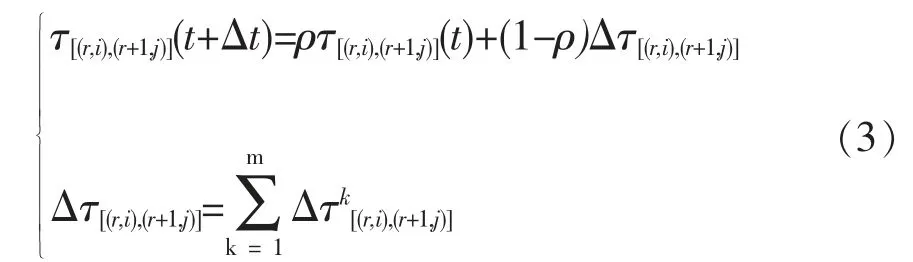
此时， 建立起安全系数与信息素之间的关联，Δτk[(r,i),(r+1,j)]的值由式（4）确定。

式中：Fsk为第k 只蚂蚁本次所搜索到的滑动面的安全系数；Q∈(1,10)为常数。

2.3 计算过程

（1）初始时刻t＝0。 对每条路径[(r,i),(r+1,j)](r＝1,…,N；i＝1,…,Mr；j＝1,…,Mr+1)，置τ[(r,i),(r+1,j)](0)=较小的正常数、Δτ[(r,i),(r+1,j)]＝0。 将m 个蚂蚁置于START 点，如图1 所示。

（2）让每只蚂蚁从START 点走到END 点，中间所走的路径根据每条路径上的概率来决定。 走完全程的路径就可作为一个边坡的滑动面进行计算，即每个蚂蚁分别独立地按式（1）计算转移概率，并追踪生成有效的滑动面。

（3）计算每只蚂蚁走过路径所生成滑动面的安全系数值Fsk(k＝1,2,…,m)，所有安全系数值中的最小值为最优解。

（4）每只蚂蚁走完一个路径后，会在其所经过的路径上留下一定的信息素，即为Δτk[(r,i),r+1,j]＝0，信息素量的大小与其路径生成的滑动面对应的安全系数值有很大关系，安全系数越小，留下的信息素量就会越大。 对各蚂蚁及路径[(r,i),(r+1,j)]，按式（2）～（4）分别计算η[(r,i),(r+1,j)]、Δτk[(r,i),(r+1,j)]和τ[(r,i),(r+1,j)](t)，然后计算转移概率。

（5）令t＝t＋1。若t≥tmax（tmax为预定的最大循环次数），则输出最佳路径（即最危险滑动面）和最小安全系数值，否则，继续搜索滑动面。

以上过程使用Fortran 语言编制蚁群算法边坡稳定程序， 在安全系数计算过程中， 使用斯宾塞（Spencer）法。

3 算例分析

3.1 基本资料

某非均质边坡[3]，剖面形状如图3 所示。 设该边坡由3 种材料组成，材料的性质如表1 所示。

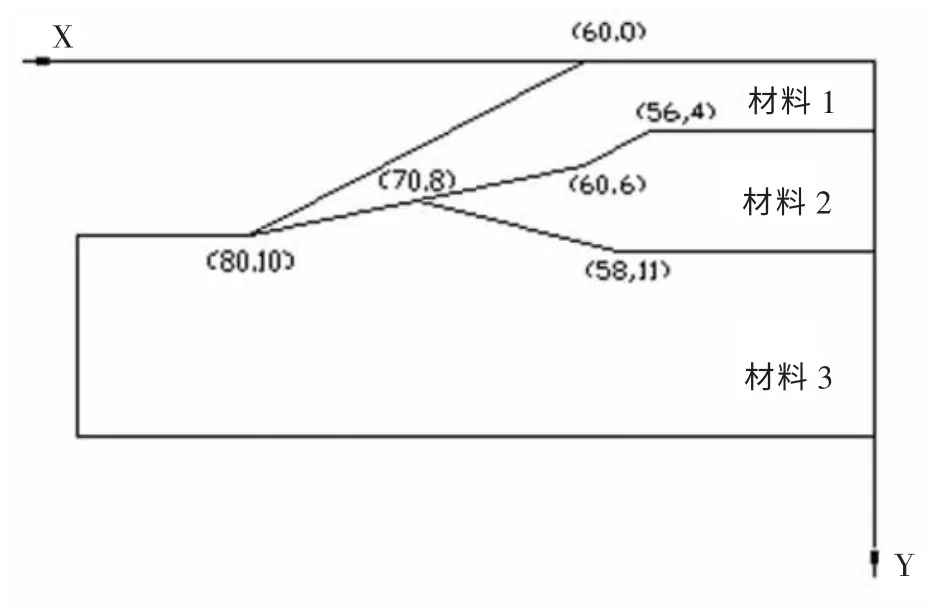
图3 非均质边坡剖面图Fig.3 Heterogeneity slope section

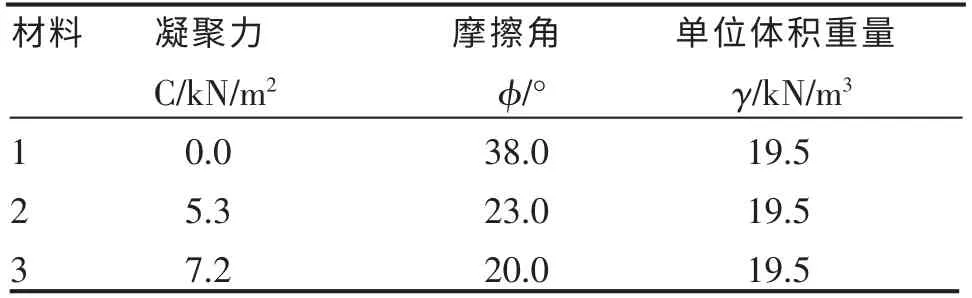
表1 边坡材料力学参数Table 1 Mechanic parameters of slope material

3.2 计算结果分析

将滑动体剖面用条分法分为21 条，条分线的间距为1.5m， 每条条分线上的节点间距为0.5m。取m=60、α=1.0、β=5.0、ρ=0.6、tmax=100，Q＝5， 运用蚁群算法进行边坡临界滑动面的搜索， 得到安全系数Fs为1.356， 最危险滑动面位置如图4 所示。对于该非均质土坡， 用遗传算法计算的结果为1.377[4]，不同方法安全系数计算结果比较如表2 所示。

从计算结果可以看出，用蚁群算法计算出的安全系数与其他方法的计算结果很近似。 这说明蚁群算法在非圆弧滑动面的搜索中是适用的，并且蚁群算法所得到的计算结果比其他方法的结果的误差更小，即蚁群算法很容易得到对应安全系数最小的临界滑动面，在精确地搜索边坡最危险滑动面及其对应的安全系数上可行的。

表2 不同方法计算边坡最小安全系数结果Table 2 The minimum safe index results of different calculation methods

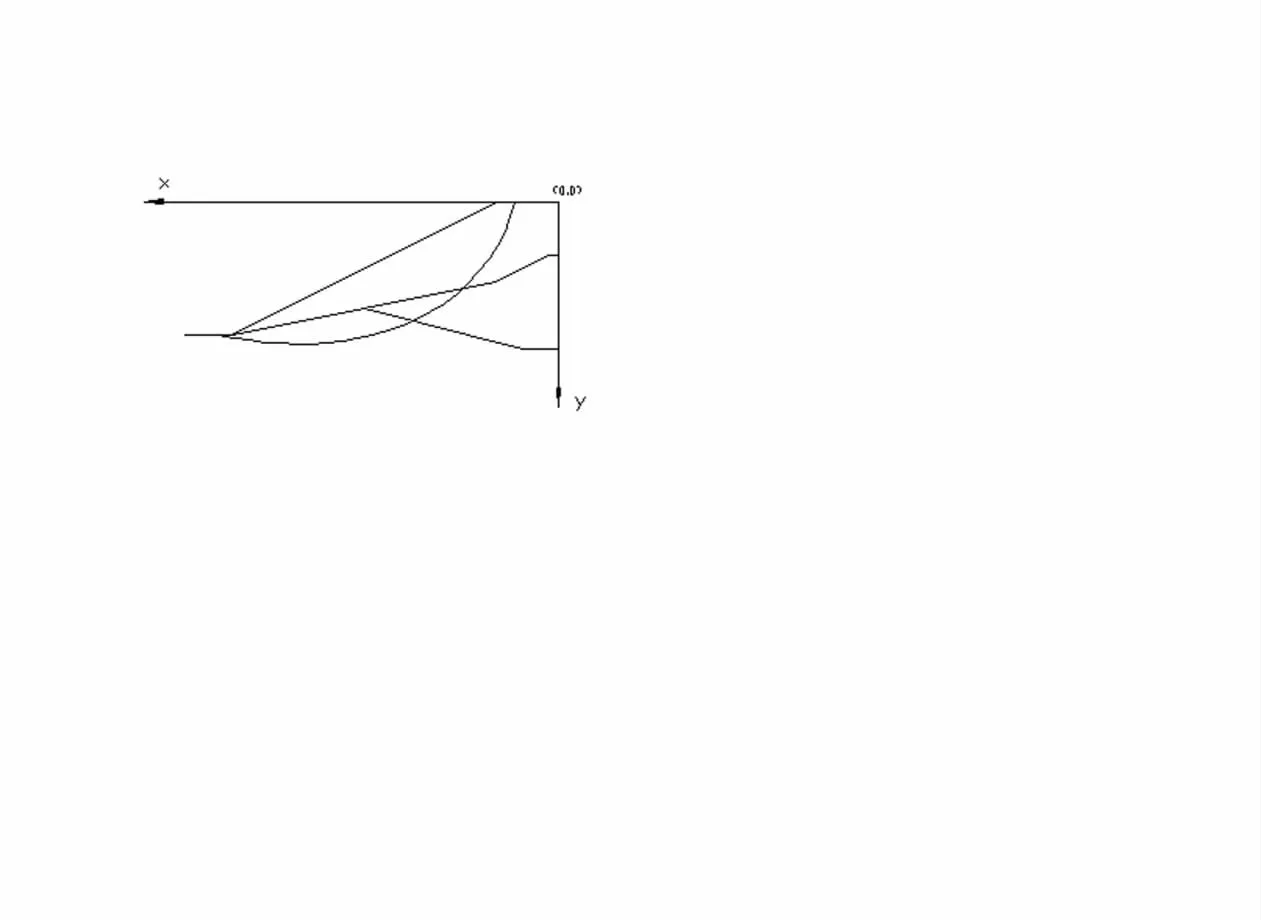
图4 临界滑裂面位置Fig.4 Critical slide plane's location

4 结语

经算例计算证明，运用蚁群算法结合斯宾塞法,在分析非均质边坡稳定性时， 能够成功地搜索到临界非圆弧滑动面及其对应的最小安全系数， 所以运用蚁群算法解决复杂边坡稳定分析问题是适用和可行的。 经与其他计算方法相比，蚁群算法算得的安全系数更小。 这说明该算法在精确地搜索边坡最危险滑动面及其对应的安全系数上具有一定的优越性。

[1] Dorigo M.Ant system：optimization by a colony of cooperation agents. IEEE Trans on SMC-Part B，1996.

[2] 钱家欢，殷宗泽. 土工原理与计算[M]. 2 版.北京：中国水利水电出版社，1997.

[3] 陈祖煜. 土质边坡稳定分析：原理、方法、程序[M]. 北京：中国水利水电出版社.2003.

[4] 温新丽，郭强. 改进遗传算法在边坡稳定非圆弧互动面搜索中得应用[J]. 浙江水利水电专科学校学报，2007（04）：51-54.