超音速大攻角子弹药气动特性数值研究＊

完颜振海，冯顺山，董永香，李顺平

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

0 引言

当处于运动状态的子母战斗部抛撒子弹药时，受抛撒力、气动力、弹道诸元等诸多因素的影响，子弹药会产生翻转运动［1］。翻转运动会严重影响子弹药的弹道性能，进而影响子弹药的可靠性和散布合理性，从而影响终点效应。

子弹药在翻转时，其攻角范围为－180°～180°，因此需要对弹体的大攻角时气动特性进行研究。大攻角时弹身绕流具有显著非线性特性，理论分析其气动特性比较困难，因此一般采用风洞试验和数值计算方法。由于攻角范围大，风洞试验需要变换支撑方式，试验周期长、成本高。目前，采用求解N -S方程模拟细长体大攻角时气动特性已经得到了广泛的应用［2－4］，计算结果也与风洞实验比较吻合，但现有数值计算的攻角范围一般小于90°，且一般只给出了特定攻角时的气动特性。文中采用激波捕捉型和激波装配型两种网格对尖拱圆柱形弹进行数值分析，由于弹体对称性取攻角范围为0°～180°。

1 数值计算方法

1.1 控制方程

积分形式的控制方程，其质量、动量和能量方程分别如式（1）、式（2）、式（3）所示［5］：

其中：Ω、S 分别是控制体的体积和表面积；ρ、v、p、fe分别为气体的密度、速度矢量、压强和体积力矢量；E、H、T分别是单位体积气体的总能、总焓和总温；qH表示外部热源为粘性摩擦应力张量。

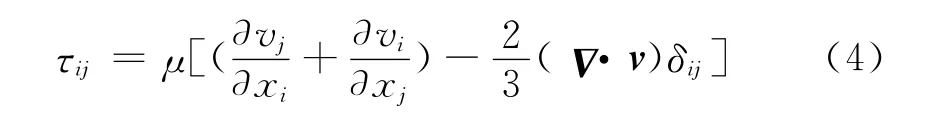
1.2 湍流模型

采用雷诺平均运输方程进行数值计算，由于引入了雷诺应力项，需要额外的湍流模型封闭方程。文中采用Shih等［6］提出的可实现k-ε两方程模型，其在附着和分离流动方面有较好的结果。

式中：Gk表示由于平均速度梯度产生的湍流动能；k、ε、μt分别表示湍流动能、湍流耗散率和涡粘性系数；σk、σε分别为k和ε的湍流普朗特数；Cε2为常数，大小为1.92。

2 数值计算模型

2.1 模型几何尺寸

文中研究子弹药的尖拱段为正切型，即圆弧段与圆柱母线相切，其外形尺寸如图1所示。

图1 模型外形尺寸图

2.2 边界条件和计算网格

采用两种不同的计算网格，一种是激波捕捉型网格，另一种是激波装配型网格。

激波捕捉型网格采用的是远场边界条件，用来获取子弹药在各攻角范围内的气动力系数，其网格如图2（a）所示，采用O O型混合网格，除了极轴附近为三棱柱网格外，其余为六面体网格，网格数为434700，其中环向69，径向70，轴向90。

激波装配型网格是在捕捉型网格计算结果的基础上建立起来的，可以更准确地反映激波形态，其网格如图2（b）所示，采用超音速速度入口和出口边界条件。由于子弹药较短和计算资源限制，仅建立半模型，未考虑大攻角时非对称性涡脱落问题。网格总数为151290，其中环向41，径向41，轴向90。

物面均采用非滑移壁面条件，对于子弹药来说，

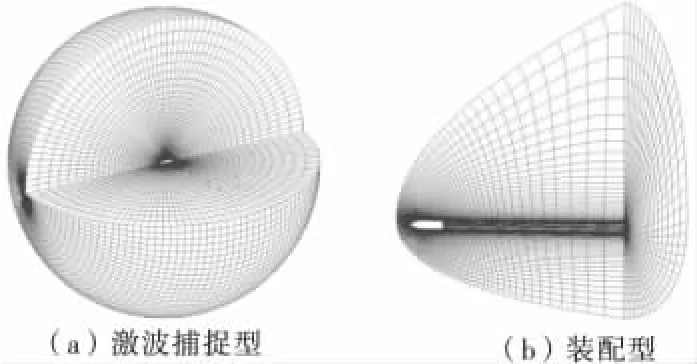
图2 计算网格图

其受到的气动力和力矩源于其表面的压力分布和剪切应力分布［5］，根据粘性流动的非滑移壁面条件，可以通过积分得到：

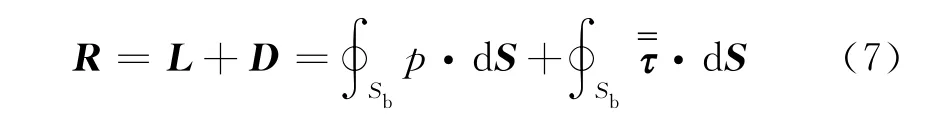
其中，R、L、D分别表示子弹受到的合力、升力和阻力；Sb表示子弹药表面积。

3 结果与分析

数值计算结果采用 Missile Datco m（以下简称Datcom）进行对比分析，Datcom是美国空军研究实验室在理论方法研究和几十年积累的试验数据的基础上开发的，其有效攻角范围0°～90°，并在α≤45°时与风洞试验结果符合很好［7－9］。

在超音速范围内，Datco m对单独弹身的法向力N和压心位置的计算采用的是Van Dyke混合理论或二阶激波膨胀波理论，对零攻角时的轴向力A的计算采用的是经验公式和Van Dyke混合理论或二阶激波膨胀波理论，对于非零攻角其采用的是Allen＆Per kins的改进横向流动理论［10］。

3.1 阻力特性

子弹药阻力系数随马赫数的变化曲线如图3所示，计算结果符合尖拱圆柱体的阻力系数分布规律。从图中可以看出，超音速范围内，阻力系数先随着马赫数的增大而增大，在Ma＝1.3时达到峰值，随后逐渐减小。

子弹药在Ma＝1.5时阻力系数随攻角变化曲线如图4所示，数值计算和Datco m在α＝0°～45°范围内相差不到5%；α＞45°时，数值计算值略高，最大相差约为12%。从图中可以看出，子弹药的阻力系数随攻角变化呈现出近似余弦曲线规律，阻力系数在攻角为85°时达到最大值，其大小约为零升阻力系数的13倍；α＝180°时（相当于钝头尖尾），阻力系数大约是零攻角（即尖头钝尾）时的2.7倍。

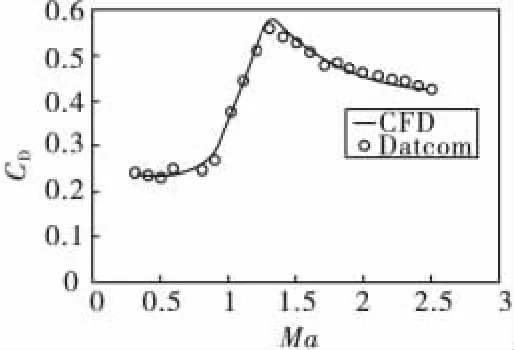
图3 阻力系数随马赫数变化曲线

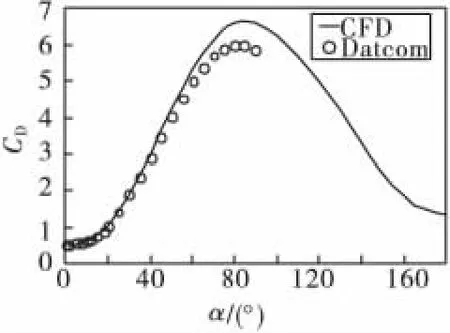
图4 Ma＝1.5时阻力系数随攻角变化曲线

3.2 升力特性

子弹药在Ma＝1.5时升力系数随攻角的变化曲线如图5所示。升力系数随攻角变化呈现出近似正弦曲线规律。升力系数在α＝50°时达到最大值，α＝130°达到最小值，零值则发生在两端以及α＝85°附近。

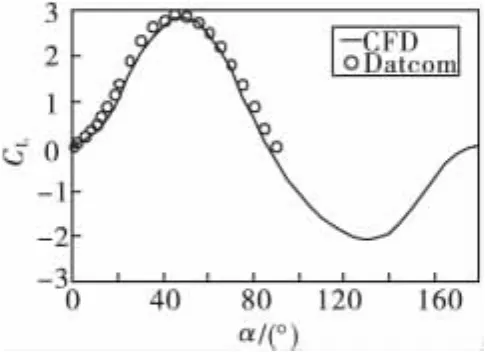
图5 Ma＝1.5时升力系数随攻角变化曲线

3.3 压心位置

数值计算和Datco m计算的压心位置对比曲线如图6所示，随着攻角的增大，压心位置逐渐后移，并在α＝180°达到最大值。

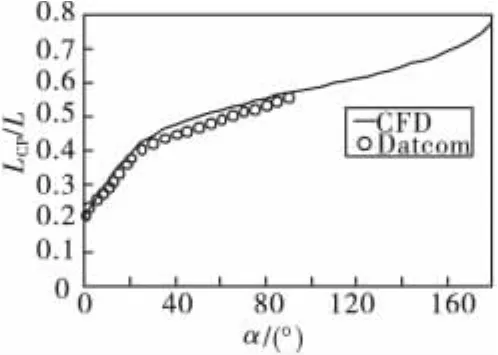
图6 Ma＝1.5时压心位置随攻角变化曲线

3.4 流场特性

流场采用数值纹影法显示，其方法是给出密度梯度大小分布图，即‖∇ρ‖［11］。数值纹影法不仅能显示间断变化的密度场（如激波），还可以给出连续变化的密度场（如尾迹、涡等）。

图7给出了子弹药纵向截面的流场形态随攻角变化图，零攻角时弹体头部形成斜激波，尖拱段末端和圆柱段后台阶处产生膨胀波，弹体的对称性还导致尾部激波。随着攻角的增大，子弹药迎流面不断扩大，头部激波的形态由圆锥形的激波变为非对称锥形激波，激波形式由斜激波逐渐变为弓形激波，同时弹体背流面发生涡脱落，如图8所示。

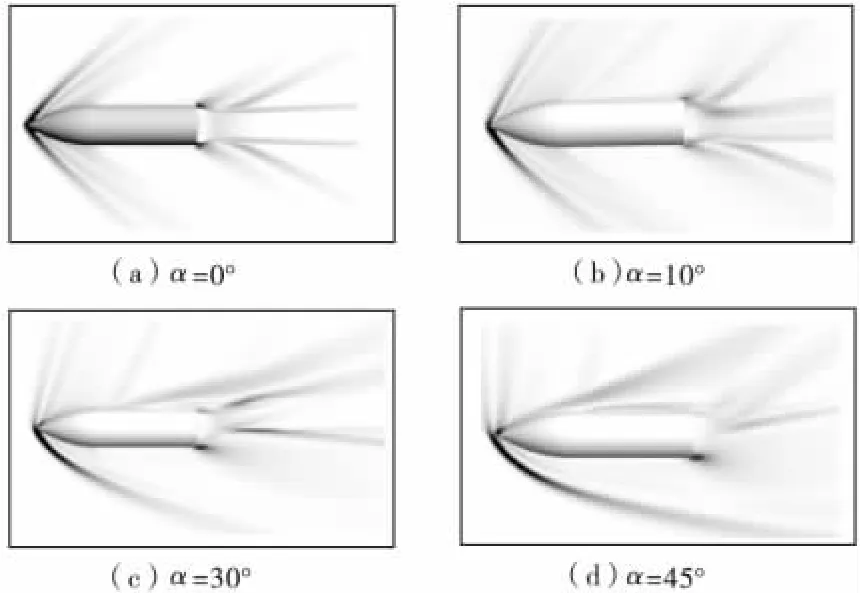
图7 纵向面流场数值纹影图

图8 攻角为30°时来流方向流场数值纹影图

4 结论

从以上分析可以得出以下结论：1）子弹药超音速气动特性随攻角的改变变化很大，攻角从0°增加到180°的过程中：阻力系数变化呈现出近似余弦曲线规律；升力系数的变化呈现正弦曲线规律；压心位置则逐渐后移。2）随着攻角的增大，尖拱形弹的头部激波的形态由圆锥形的斜激波逐渐变为非对称锥形弓形激波，同时弹体背流面发生涡脱落。

［1］ 杨启仁.子母弹飞行动力学［M］.北京：国防工业出版社，1999.

［2］ Hsieh T，Priolo F J，War dlaw A B.Calculations and comparisons of the flowfield about an ogive cylinder at M＝3.5［J］.Jour nal of Spacecraft and Rockets，1993，30（6）：665－673.

［3］ Josyula E.Co mputational Simulation i mprovements of supersonic high angle－of－attack missile flo ws［J］.Jour nal of Spacecraft and Rockets，1999，36（1）：59－66.

［4］ 邓有奇，周乃春，胡汉东.尖拱弹身大攻角N S方程数值计算［J］.空气动力学学报，2000（z1）：109－114.

［5］ Charles Hirsch.Numerical computation of internal and exter nal flows［M］.Oxfor d：Elsevier’s，2007.

［6］ Shih T H，Liou W W，Yang Zhigang，et al.A new k－ε eddy viscosity model f or high Reynolds number tur bulent flows［J］.Co mputers Fluids，1995，24（3）：227－238.

［7］ Blake W B.Missile datcom：1997 status and future plans，AIAA－1997－2280［R］.1997.

［8］ Simon J M，Blake W B.Missile datcom：high angle of attack capabilities，AIAA－1999－4258［R］.1998.

［9］ Abney E J，Mc Daniel M A.High angle of attack aerodynamics predictions using missile datcom，AIAA－2005－5086［R］.2005.

［10］ Blake W B.Missile datco m：apllications to projetiles，AIAA－1989－3370［R］.1989.

［11］ James DeSpiritio，Peter Plostins.CFD prediction of MP910 pr ojectile aerodynamics：unsteady wake effect on Magnus moment，AIAA－2007－6580［R］.2007.