边缘分布估计算法在车削参数优化中的应用

谢书童 郭隐彪

厦门大学,厦门,361005

0 引言

数控加工的主要目的是节约加工成本、提高加工效率、提高工件加工质量。在给定加工约束条件下,如何选择最优加工参数(集)来达到节约加工成本目的(即带约束的最小化问题),是一个具有重要实际意义的研究课题。以往对加工参数的优化通常采用传统的数学处理方法(如动态规划、线性或非线性规划算法)寻求问题的最优解[1],然而大量的加工参数优化问题是多约束非线性的复杂问题,利用这些方法很难取得最优解。另外,随着现代启发性算法(meta—heuristic algorithm)的迅速发展和广泛应用,不少学者将其应用在机械领域的加工参数优化问题中,利用它们搜索问题的次优解。文献[2-3]运用蚁群算法(ACO)解决车削参数优化问题,文献[4]则采用粒子群算法(PSO)来解决同样的问题,文献[5-7]先后使用改进的遗传算法(GA)来实现车削参数的优化选择。模拟退火算法(SA)在文献[8]中也被用来解决同样的优化问题。但是每种启发性算法都有各自的局限性,遗传算法使用交叉算子和变异算子对种群中的个体进行随机的交叉和变异来产生下一代,这种做法带有一定的盲目性,会破坏个体中的优秀基因,导致算法收敛于局部最优解。同时,遗传算法、粒子群算法、蚁群算法等基于种群的进化算法在解决复杂优化问题时是通过种群中的每一个个体的进化(即所求问题的解的迭代)来实现的,它们侧重于从“微观”层面对问题进行数学建模。而分布估计算法(estimation of distribution algorithms,EDAs)[9-12]中没有传统的交叉和变异等操作,取而代之的是通过一个概率模型来描述种群所表示的解的分布,采用统计学习手段从群体“宏观”的角度对问题进行数学建模,所以分布估计算法是一种把进化算法和统计学习有机结合的全新进化算法。此外,分布估计算法还通过概率模型来描述变量之间的关系,从而能有效地解决非线性、变量耦合的优化问题。本文采用基于分布估计算法的优化方法来解决多道车削加工参数的优化问题,实现最小化加工成本的目标。

1 车削参数优化问题的数学模型

对于多道车削加工参数优化问题,因为文献[8]提出的数学模型考虑了大量的实际加工约束条件,更接近实际加工,因此本文采用该数学模型。待优化的车削参数组合包括粗切削速度vr、粗进给量 fr、粗车量(粗车深度)dr、精切削速度vs、精进给量 fs和精车量(精车深度)ds。(单个)工件加工成本CU主要由4个部分组成,即实际切削过程中的加工成本CM、工件装卸操作和刀具空走所用成本CI、换刀操作成本CR、刀具磨损成本CT,所以

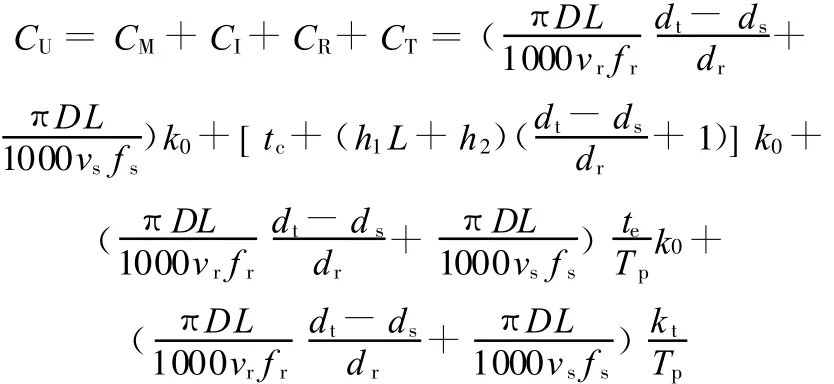
式中,k0为单位时间的工人成本和管理成本之和,美元/min;D、L分别为工件的直径和长度,mm;dt为车削总余量,mm;h1、h2分别为与车刀空走时间和进刀/退刀时间有关的常量;tc、te分别为工件装卸的时间、换刀时间,min;TP为刀具(粗、精)权重寿命,min;kt为刀具成本,美元/edge。

粗车次数为

本文研究的目标是在约20个接近实际加工的粗精车削约束条件下,最小化CU(vr,vs,fr,fs,dr,ds,n)。约束条件包括[7-8]:①vr、vs、fr、fs、dr、ds的上下限约束;②刀具寿命约束;③切削力、切削功率和表面粗糙度约束;④稳定切削面积约束以及切屑和刀具接触面温度约束;⑤粗车参数和精车参数的相关性约束。

2 算法

分布估计算法是一种新兴的基于种群的进化算法[9-11],其基本思想是将输入变量xi看作一个随机变量,所有的输入变量构成一个随机矢量x=(x1,x2,…,xk),这时一个个体就是该随机矢量的一个取值,而一个群体就对应于随机矢量的一个分布。利用联合概率分布捕捉变量之间的依赖关系,并在此概率分布上进行采样以得到更优的群体[10—12]。分布估计算法中有多种概率模型,如单变量、双变量、多变量(三个或三个以上)相关,本文采用单变量模型来估计种群分布,这种算法称为单变量边缘分布算法(univariate marginal distribution algorithm,UMDA)[10]。算法中随机矢量的联合概率分布为单个随机变量的概率分布乘积:

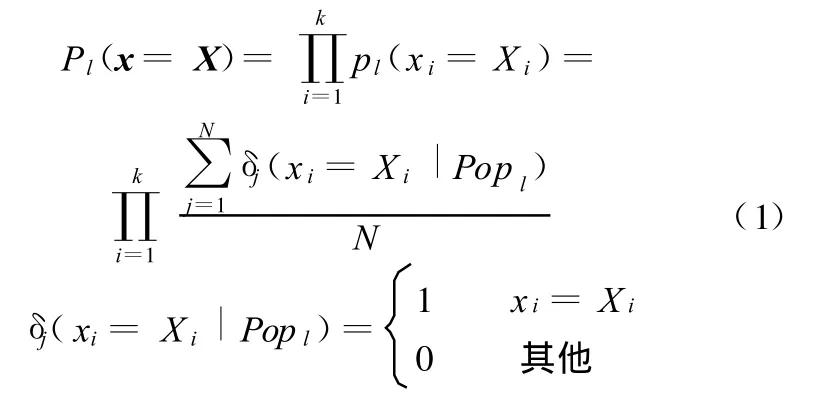
式中,l为种群代数;k为问题维数(待优化的变量个数);N为种群大小;Popl为优秀子种群。

2.1 概率矢量和算法框架

概率分布矢量PV由待优化变量 ——粗切削速度vr、粗进给量 fr、精切削速度vs、精进给量 fs和精车量ds依次相连而成,每个变量用20位二进制表示,共100位。概率分布矢量PV以每一位的值为0.5来初始化。此外,待优化变量dr可由ds与式(1)通过遍历算法算出。

本文提出两个基于UMDA的算法,一个是基于基因修复策略的边缘分布估计算法(UMDArp),该算法具有基因修复和惩罚函数两种约束条件处理方法,其基本流程如图1所示,主要步聚如下:

(1)使用概率矢量PV(0.5,0.5,…,0.5),采样产生N个个体的初始种群,并计算每个个体的适应值。

(2)选出适应值最高的M个个体,作为优秀子种群。

(3)根据选出的M个个体,估计出新的概率分布PV,然后利用概率分布PV,采样产生新一代的N个个体。

(4)判断迭代数gen是否超过最大代数的一半(MaxGen/2),若超过,就启用基因修复功能,加快算法后期的收敛。

(5)计算每个个体的适应值,迭代数加1。

(6)判断算法是否达到最大迭代数MaxGen,若是,输出优化种群;否则转(2)进入迭代。

另一个算法是只有惩罚函数的无基因修复策略的边缘估计算法(UMDAp),其算法框架与UMDArp基本一致,只是没有基因修复功能。

2.2 约束条件处理

2.2.1 惩罚函数

针对模型中的约束条件,采用惩罚函数对违反约束条件的个体进行惩罚,即把不满足约束的个体的适应值降低。破坏不同的约束条件,施以不同程度的惩罚,惩罚函数如下:

由于是最小化问题,所以加工成本函数CU(X)值越小,赋以越大的适应值,适应值函数可表示为

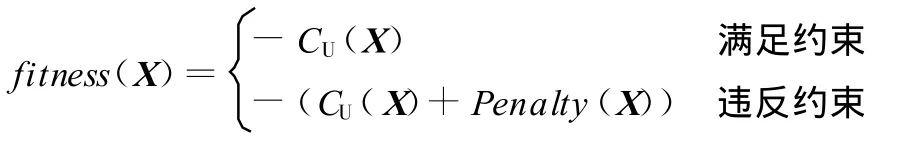
UMDAp算法采用式(2)进行惩罚,而UMDArp算法则不用其中约束条件n=(dt—ds)/dr的惩罚,用基因修复策略代替,其他约束惩罚与UMDAp相同。

2.2.2 基因修复

在采样产生新一代种群时,不少个体基因中的精车量ds虽然满足其上下限,但是会导致粗车次数n不为整数,或者粗车量dr超过可行上限,产生了非法解。解决这三个变量相互约束的方法除了上述的惩罚函数,本文提出了基因修复策略,对个体中的不良基因精车量ds进行修复,即重新调整精车量ds,使其同时满足三者之间约束条件。例如,在后继的算例中,精车量 ds∈[1,3],随着种群的进化,会产生基因中的ds落在(2,3)范围内的个体,假定其值为2.4。此时,dt=6,dr∈[1,3]。那么n=(dt—ds)/dr=3.6/dr,若要满足这个方程的话,要么使dr=3.6,但dr超过可行上限;要么使n不为整数,这又破坏了粗车次数为整的约束,产生不可行解。若此时对这不良基因进行修复,把ds(2.4)修改成[1,2]内的随机数,则此个体很可能变成可行解,甚至变成优化解。这有助于解决可行解较稀疏的多约束问题,是惩罚函数做不到的。因为粗车次数n是一个小整数,所以调整dt、ds和n三个变量同时满足约束难度不大,这也是采用基因修复的一个原因。基因修复和惩罚函数相结合的约束处理方案使得 UMDArp算法取得成功。此外,文献[2,5]算法正是因为没有考虑ds的正确取值,故而出现了粗车次数不为整数的偏差结果,后来分别由文献[3,6]对其进行了修正。

3 模拟实验

UMDArp和UMDAp算法用MAT LAB实现,参数设定如下:种群大小为2000、迭代数为50、截断选取率为0.9。测试其性能的加工例子来自于文献[7-8],如表1所示,其中一些变量的含义也可参见文献[7-8]。两个算法均在Windows平台(CPU为 PⅣ2.0GHz、内存为1GB)上运行1000次,取平均值。并与以往提出的算法SA/PS[8]、FE —GA[6]、GA[7]、ACO[7]和 PSO[4]的结果进行了比较,如表2所示。

表1 车削实例的条件参数[7-8]

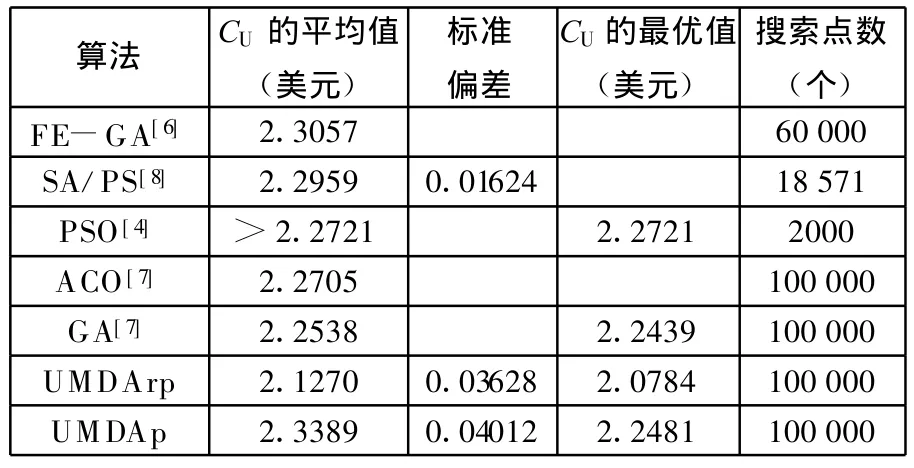
表2 不同算法的结果比较

从表2的加工成本CU的平均值来看,由本文UMDArp算法得到的结果比采用遗传算法GA[7]得到的结果节约了5.6%的加工成本,比采用FE—GA[6]、SA/PS[8]、PSO[4]和 ACO[7]等算法得到的结果节约更多。相似地,UMDArp算法也找到了加工成本很低的CU最优解2.0784美元,与其他算法找到的最优解相比,降低了约0.2美元或0.16美元(每工件)的加工花销。这均表明UMDArp算法能更有效地解决车削参数优化问题。而UMDAp所得的加工成本CU的平均值则不太理想,但还是找到不错的最优解。最后,表3列出UMDArp算法找到的部分优化解。

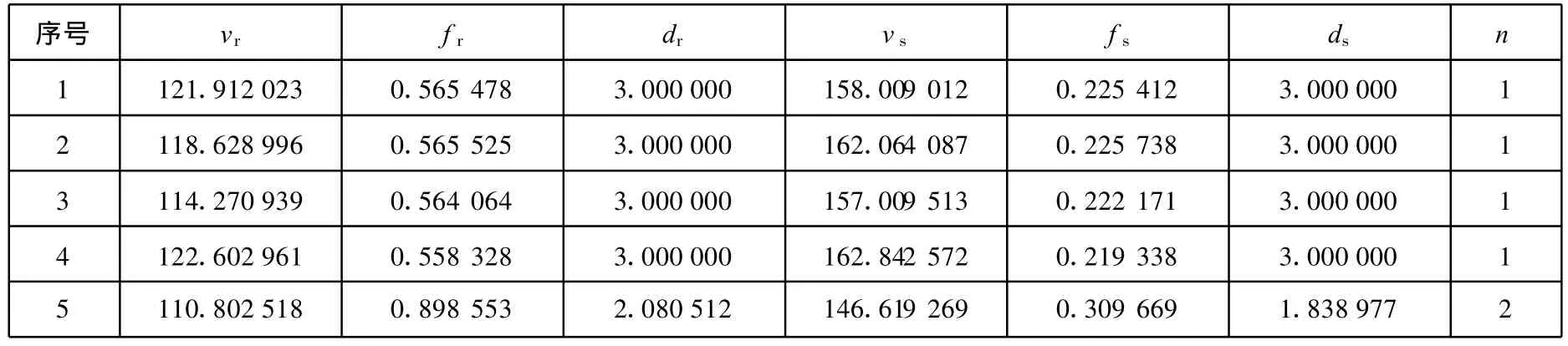
表3 UMDArp的部分解

4 结论

(1)针对最小化加工成本的车削参数优化问题,提出了两个基于边缘分布估计的UMDArp和UMDAp算法。通过计算机模拟表明,UMDArp算法比以往提出的模拟退火算法(SA)、遗传算法(GA)、蚁群算法(ACO)和粒子群算法(PSO)具有更强的搜索能力,找到了更优的车削参数集,降低了加工成本。

(2)在约束条件处理方法中,所采用的基因修复策略和惩罚函数相结合的方案优于只用惩罚函数的方案。

此外,只有惩罚函数的约束处理方法的UMDAp算法也能找到较好的最优解。基于边缘分布估计的概率模型是分布估计算法中简单的概率模型。因此,采用更复杂的多变量相关的贝叶斯网络(Bayesian networks)概率模型求解这一问题将是我们未来的研究工作。

[1]Mukherjee I,Ray P K.A Review of Optimization Techniques in M etal Cutting Processes[J].Computers&Industrial Engineering,2006,50(1/2):15-34.

[2]Vijayakumar K,Prabhaharan G,Asokan P,et al.Optimization of M ulti—pass Turning Operations Using Ant Colony System[J].International Journal of Machine Tools&Manufacture,2003,43(15):1633-1639.

[3]Wang Y C.A Note on‘Optimization of Multi—pass Turning Operations Using Ant Colony System'[J].International Journal of Machine Tools&Manufacture,2007,47(12/13):2057-2059.

[4]Srinivas J,Giri R,Yang S H.Optimization of Multi—pass Turning Using Particle Swarm Intelligence[J].International Journal of Advanced Manufacturing Technology,2009,40(1/2):56-66.

[5]Onwubolu G C,Kumalo T.Optimization of Multipass Turning Operations with Genetic Algorithms[J].International Journal of Production Research,2001,39(16):3727-3745.

[6]Chen M C,Chen K Y.Optimization of Multipass Turning Operations with Genetic Algorithms:a Note[J].International Journal of Production Research,2003,41(14):3385-3388.

[7]Sankar R S,Asokan P,Saravanan R,et al.Selection of Machining Parameters for Constrained Machining Problem Using Evolutionary Computation[J].International Journal of Advanced Manufacturing Technology,2007,32(9/10):892-901.

[8]Chen M C,Tsai D M.A Simulated Annealing Approach for Optimization of Multi—pass Turning Operations[J].International Journal of Production Research,1996,34(10):2803-2825.

[9]Muhlenbein H,Paass G.From Recombination of Genes to the Estimation of Distribution Part 1,Binary Parameter[C]//4th International Conference on Parallel Problem Solving from Nature—PPSN IV.Berlin:Springer—Verlag,1996:178-187.

[10]M uhlenbein,H.The Equation for Response to Selection and Its Use for Prediction[J].Evolutionary Computation,1997,5(3):303-346.

[11]Larranaga P,Lozano J A.Estimation of Distribution Algorithms:a New Tool for Evolutionary Computation[M].Boston:Kluwer Academic Publisher,2002.

[12]Lozano J A,Larranaga P,Inza I,et al.Towards a New Evolutionary Computation:Advances in the Estimation of Distribution Algorithms[M].Berlin:Springer—Verlag,2006.