小波变换去噪处理在曲面重构中的应用

杨征宇 夏庆观 缪德建

南京工程学院先进数控技术江苏省高校重点建设实验室,南京210013

0 引言

数字化制造是先进制造技术的重要内容之一,其目的是使企业的集成计划、产品评估和所有制造过程以及资源配置与产品相结合[1]。自由曲面重构是数字化制造的重要支撑技术之一,广泛应用于航空、塑料、汽车、模具工业和医疗、地质研究等领域的型面数据处理,但自由曲面加工(误差)预测尚未得到深入研究[2]。在产品模型的数字化过程中,生成的大量产品曲面型值点坐标数据会因为测量误差、操作误差等而产生噪声[3],因此,重构曲面需要采取去噪处理措施,以避免用扭曲的曲面去满足每个型值点,这对提高曲面重构精度乃至重构效率具有重要意义。然而,目前有关曲面重构中去噪声处理的研究文献很少。

本文对含噪声的原始曲面的型值点数据进行小波分解,提取其低频分量,进行去噪处理,在此基础上利用UG的NURBS功能对处理过的数据进行曲面重构,并对曲面重构精度进行检测,采用工程实例对该方法进行了验证。该方法在曲面重构精度和效率方面取得了满意的效果。

1 曲面重构中的小波变换去噪处理方法

1.1 原始曲面

本文利用MATLAB软件平台,用球面进行仿真实验,球面的参数方程为[4-5]

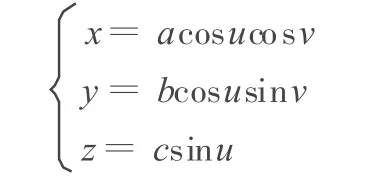
式中,a、b、c为常数,a=2,b=3,c=1;、u、v为参变量,u、v=iπ/150,i=0,1,2,…,15。

图1a所示为仿真实验的原始曲面,曲面u方向和v方向组成16×16个网格交点,交点的数值是曲面型值点数据,图1b所示为含噪声的曲面。

1.2 曲面的小波去噪

图2a、图2b所示为原始曲面u方向型值点数据和含噪声曲面u方向的原始型值点数据。对含噪声的原始型值点数据进行3层db1小波分解,图2c～图2e所示分别为含噪声原始型值点数据的第1层小波低频、第2层小波低频和第3层小波低频,这3层小波低频不同程度地对噪声进行了抑制。可以看出,第3层小波低频滤除噪声的效果较好。

1.3 曲面重构

分别将含噪声的原始曲面型值点的第1层小波低频、第2层小波低频和第3层小波低频构成u、v方向16×16个网格交点的数值,利用MATLAB软件对这些数值进行曲面重构仿真。如图3所示,图3c的曲面非常逼近图2a的原始曲面。

1.4 使用NURBS重建曲面

将图3a～图3c小波低频曲面上的16×16个网格交点的数值,构成u或v方向16条NURBS曲线,利用UG软件的NURBS曲面工具条上的“通过曲线组”重建曲面,并且处理成曲面光顺效果图,如图4所示。图4c第3层小波低频重建曲面的光顺效果优于图4a、图4b的第1层小波低频和第2层小波低频的重建曲面的光顺效果。

1.5 重构曲面的误差分析

数据曲线拟合也是消除散乱点或噪声的方法,本文利用MAT LAB的 polyfit函数对图1b所示含噪声的原始型值点数据进行二阶多项式拟合,获取256个拟合数据。限于篇幅,本文给出其中u方向第10条16个含噪声的原始型值点数据的拟合曲线,如图5所示。

以图1a中256个原始型值点数据为均值,256个拟合数据的标准差为0.0031,图2e第3层小波低频的256个数据的标准差为0.0027。可见,对原始曲面含噪声的型值点数据进行小波变换所获得的型值点数据曲线低频分量的误差相对较小。

2 工程应用实例

2.1 曲面重构中的小波变换去噪处理流程

上述重构曲面误差分析是以无噪声的原始曲面型值点数据的均值进行标准差分析的。在逆向工程的实际应用中,往往采集到的是含噪声的曲面型值点数据。本文将采集到的含噪声的曲面型值点数据进行二阶多项式拟合,将得到的二阶多项式拟合数据作为均值,将含噪声的原始型值点数据对二阶多项式拟合的数据进行标准差处理。同时,对采集到的含噪声的曲面型值点数据进行小波分解,提取低频型值点数据并进行二阶多项式拟合,将得到的二阶多项式拟合数据作为均值,将小波分解的低频型值点数据对二阶多项式拟合的数据进行标准差处理。小波变换的层数可以取决于标准差,并借助NURBS重建曲面的光顺效果来决定。图6是曲面重构中小波变换去噪处理的流程图。

2.2 实例验证

本文以某轿车行李箱外板冲压模具的加工为工程实例,对上述理论研究进行验证。图7所示是行李箱外板的产品零件数字模型,采集试验零件实体模型的外型面型值点坐标数据,使用设备为意大利生产的泡利 EL—1018三坐标测量机(工作行程为4000mm×2700mm×1700mm,控制系统为PC—DMIS)。

在零件基准点系统(reference point system,RPS)设置的坐标系中,沿X、Y方向以50mm的行距取坐标(x,y,z),所取坐标点数为1186。将疑似误差坐标点数据人为增大8倍,用UG系统对得到的重构曲面进行光顺分析,结果如图8所示,由图8可见曲面明显不平整。

将1024个含噪声的原始型值点数据依次排列组成行向量,进行二阶多项式拟合,获取1024个拟合型值点数据,并将含噪声的原始型值点数据相对拟合型值点数据进行标准差处理。对含噪声的原始型值点行向量进行3层db1小波分解,提取第3层小波低频数据,并且对小波低频数据进行二阶多项式拟合,获取1024个小波低频拟合数据,将小波低频处理后的型值点数据对拟合型值点数据进行标准差处理。含噪声的原始型值点行向量对拟合型值点数据的标准差为0.0056;小波低频数据对小波低频拟合数据的标准差为0.0042。利用小波低频数据进行NURBS重构后的产品曲面如图9所示。图10所示为再次试模的工况,冲压得到的冲压零件的光顺性达到了产品设计要求。

3 结语

曲面型值点数据处理是决定曲面重构精度和重构效率的关键技术,本文对原始曲面含噪声的型值点数据进行小波变换,获取型值点数据的低频分量,然后用NURBS曲线拟合曲面,实现曲面的重构。小波变换去噪方法的仿真实验和在汽车模具设计与制造中的工程验证都表明,该方法能够较好地改善产品零件原始曲面的拟合精度,具有实际应用价值。

[1]Koeth C P.Die Branche vor der Naechsten Revolution[J].Automobile Industrie,2003,7:102-109.

[2]Li Yadong,Gu Peihua.Inspection of Free—form Shaped Parts[J].Robotics and Computer—integrated Manufacturing,2005,21(4/5):421-430.

[3]Choi B K.Surface Modeling for CAD/CAM[M].New York:Elsevier Science Publishers,1991.

[4]Mallat S.信号处理的的小波导引[M].杨力华,戴道清,黄文良,等,译.北京:机械工业出版社,2002.

[5]冉启文.小波变换与分数傅立叶变换理论及应用[M].哈尔滨:哈尔滨工业大学出版社,2001.