面向制造的连续体结构拓扑优化设计方法研究

王明强 李治多

江苏科技大学,镇江,212003

0 引言

随着拓扑优化理论的发展和拓扑优化工具的出现,拓扑优化已开始在航空、汽车等工程领域得到逐步应用。在拓扑优化中引入制造工艺约束使得优化技术更具吸引力,制造工艺约束是在概念设计阶段需要考虑的重要因素。因此,拓扑优化作为一种产生设计概念的工具,可进一步实现与制造约束的集成,这对缩短概念设计和工程实现之间的距离有重要意义[1]。然而拓扑优化毕竟处于结构的概念设计阶段,其结果对于后续的设计与分析过程仅有概念性的指导意义,拓扑优化结果的工程可利用性问题已经成为制约拓扑优化进一步发展的障碍之一[2]。

近几年,国内外学者对结构拓扑优化问题开展了广泛的研究。Thomas[1]在基本设计阶段考虑制造约束,用数学优化技术结合基于结构分析的有限元技术实现了设计的最优拓扑布局,完成了有益的轻量化要求,并将其用于压模、铸模及板金结构的优化中。Harzheim等[3]采用基于CAO和SKO的算法并考虑制造工艺约束,获得了更容易理解的设计方案。陈义保等[4]提出了一种新的带有制造工艺约束的多约束结构拓扑优化设计模型。左孔天[2,5]提出了基于工程约束思想的结构拓扑优化,通过在优化模型中加入制造加工约束来减小设计空间,确保工程可接受的及可制造的拓扑优化结果。

针对传统结构拓扑优化的结果在工程上难以制造加工的问题,为更好地处理在概念设计阶段连续体拓扑优化结果的工程实用化问题,提出了一种基于制造工艺约束的结构拓扑优化设计的方法,即面向制造的分级优化方法,使优化结果既满足工程设计性能要求,又同时满足制造加工性能的要求,以实现面向制造的结构拓扑优化设计。

1 面向制造的分级拓扑优化方法

面向制造的分级拓扑优化方法的思想是,采用分级优化策略处理带制造工艺约束的拓扑优化问题。第一级优化从设计角度,确定结构拓扑优化结果的基本拓扑构型,以满足设计性能要求;第二级优化针对第一级优化所得的拓扑结果,进行制造可行性分析和加入制造工艺约束的二次拓扑优化,以获得面向制造的拓扑优化结果。分级拓扑优化的实现流程如图1所示。不直接在第一级优化中引入制造约束的原因在于,没有针对性,可能获得的只是局部最优。采取分级优化可以保证全局最优,使拓扑优化结果同时满足设计要求和制造要求,具有工程应用价值。

2 面向制造的连续体拓扑优化模型

2.1 基于制造约束的SIMP法拓扑优化模型

在面向制造的分级拓扑优化策略实现中,采用固体各向同性惩罚材料(solid istropic material with penalization,SIMP)模型[6]。该优化模型的目标函数为结构的整体柔度最小即刚度最大,设计变量为单元密度,约束条件为体积约束和制造工艺约束,则拓扑优化模型为

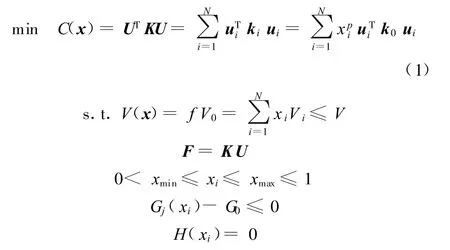
2.2 成员尺寸控制约束及处理策略

制造工艺约束包含成员尺寸控制约束、拔模约束、挤压约束、模式组(各种对称约束)及模式重复等约束。这里从面向制造的优化角度出发,以成员尺寸控制约束为例,分析制造工艺约束的实施及处理策略。

成员尺寸控制约束分为最小成员尺寸约束和最大成员尺寸约束。最小成员尺寸约束是指优化结果中单元密度为1的区域的允许最小尺度。零部件在设计制造加工过程中,往往有一个最小尺寸要求,小于该尺寸范围的特征,将很难铸造或用刀具加工。因此在零件的初始概念设计阶段就应考虑这一要求,针对零件不同的加工要求加入不同的最小成员尺寸约束。这里给出最小成员尺寸控制法的数学模型:

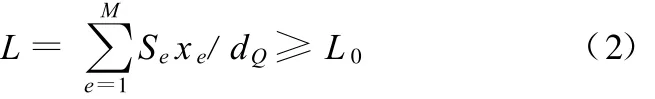
式中,L为离散边界单元孔洞的等效特征尺寸;Se为边界单元e的外表面积;dQ为边界孔洞相对于投影平面Q的平均深度;M为边界离散单元数;L0为加工尺寸下边界。

这里投影面Q定义为需要控制加工尺寸约束所在的纵向平面(YZ平面)。通过在优化模型中引入最小加工尺寸约束的下限值,来对结果中的最小特征的结构尺寸进行控制。引入最小成员尺寸约束可以获得比较均匀的材料分布,便于铸造过程材料的流动或提供足够刚度以便于刀具加工。

最大成员尺寸约束针对的是优化结果中单元密度为1的区域。在该优化区域中各向尺度不能全部大于该尺寸,这样可以消除优化结果中的材料堆积,避免制造过程引起的产品缺陷(如铸造过程中散热不均匀),并能提供多个传力路径以提高产品可靠性。

对于最小/最大成员尺寸约束的实施,采用一种新的处理策略,即在第二级优化中对不可行子域,通过圆域进行拟合以缩减原始设计空间,实现最小/最大成员尺寸约束的控制,其处理规则为

其中,(X,Y)为设计域单元坐标;(X0,Y0)为不可行子域中心坐标;Lmin、Lmax分别为最小成员尺寸和最大成员尺寸,其值可根据实际制造加工要求来定。一般,最小成员尺寸要大于3倍的单元平均尺寸,最大成员尺寸至少为单元平均尺寸的6倍。

2.3 基于制造约束的优化模型求解

加入制造工艺后的拓扑优化问题变为一个多约束优化问题。拓扑优化数学模型求解算法中的移动近似算法(method of moving asymptotes,MMA)[7]广泛应用于具有制造约束、工程约束等复杂多约束拓扑优化问题的求解[5]。但采用此法会增加优化求解问题的复杂性,这通常会导致计算得不到有用的工程可行解[5]。

为了降低求解的难度,采用优化准则法(optimization criterion,OC)求解含制造约束的拓扑优化模型。对于柔度最小的优化问题采用比MMA法收敛速度快的OC法。综合文献[8],给出改进的OC法更新设计变量的迭代格式:

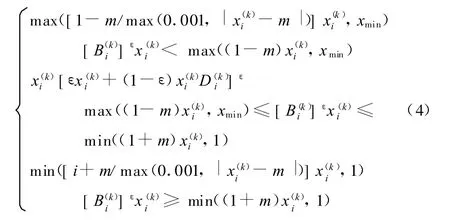
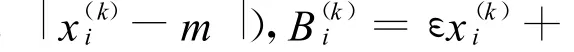
2.4 数值不稳定的去除方法

拓扑优化过程中出现的数值不稳定问题实际上是由数值计算中场函数的一种数值不稳定现象或由数值奇异解造成的,其表现形式包括棋盘格式、多孔材料、网格依赖性、局部极值等。多孔材料和棋盘格式导致计算结果的可制造性差,网格依赖性使计算结果的可靠性下降,局部极值问题导致计算得不到全局最优解或得不到工程可行解。拓扑优化中数值计算不稳定性的消除非常重要,它关系到数值计算的收敛性和计算结果的可制造性。

滤波过滤法对消除棋盘格式简单有效,并能保证一定的网格无关性,但优化结果中存在明显的“边界扩散”效应,并可能形成一种点态的密度场[9]。密度和敏度混合的过滤技术具有敏度过滤技术的优点,还可以提高密度场光滑性和连续性,该法在一定程度上可以消除“边界扩散”效应,同时能有效消除棋盘格式并使结构体现出较好的网格无关性[7]。窗函数法相当于将不同的窗函数作为卷积核与原有数字信号进行卷积,其物理意义较直观,且可根据原数值解的具体情况灵活选择窗函数的尺度参数,易于编程实现。窗函数法采用高斯窗函数对密度场分布函数进行处理,以解决棋盘格式问题,其实质是滤波法的一种[6]。

综合上述分析,为了更好地解决在拓扑优化过程中优化结果的“边界扩散”效应问题,并在解决棋盘格式问题的同时提高收敛速度,减少计算量,本文对密度和敏度混合过滤进行改进,从工程实际应用角度出发,采用密度和敏度混合高斯滤波法。

2.4.1 密度和敏度混合高斯滤波法

混合过滤技术将每个节点的密度用周围单元密度的加权平均值来近似,从而提高密度场的光滑性和连续性,再对处理后的密度进行敏度的卷积,以改善有限元求解的收敛性和解的存在性。

将敏度过滤技术中的密度用设计变量的平均密度代替;为了提高权函数的光滑性,密度和敏度混合过滤法中的权函数w(xi)=max(He,0)由高斯函数代替,即

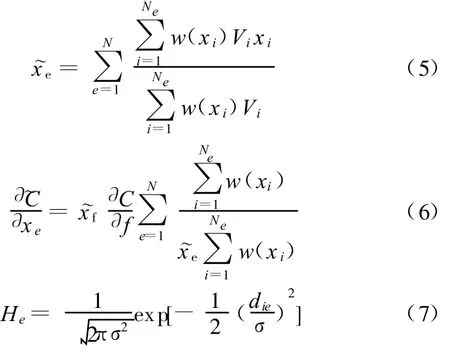
其中,die为单元i和单元e中心的距离;~xe和~xf分别为过滤前后单元的平均密度;σ为高斯函数的尺度参数(决定了过滤函数的平滑程度),σ=rmin/2;rmin为过滤半径,即表示优化结果的最小尺寸为单元尺寸的rmin倍;Ne为过滤半径之内单元的数目。过滤半径的取值应随着单元网格密度的增大而适当有所增大。

2.4.2 基于密度和敏度混合高斯过滤法算例

基结构如图2所示,其中 L=10mm,集中载荷F=10kN,材料弹性模量E=200GPa,泊松比ν=0.3,惩罚因子 p=3.0,过滤半径rmin=1.5mm,移动极限初始值m=0.2。在相同初始优化参数条件下,采用提出的不同过滤方法,其优化结果如图3所示。

图3a、图3b所示为采用本文提出的混合过滤技术的优化结果。从图3中优化结果可以看出,所提出的过滤法能很好地消除棋盘格式和网格依赖性等数值不稳定性现象且边界清晰。但采用密度和敏度混合过滤结果会出现一定程度的“边界扩散”现象,如图3a所示,在虚线圆形区域内,边界局部产生了细小的传力路径,这将降低结构的可靠性。采用密度和敏度混合高斯过滤法可以很好地解决此问题,结果如图3b所示,该结果与参考文献[8]的优化结果非常一致,并且比文献[11]优化结果(图3c)的边界更加清晰。

3 面向制造的分级优化法算例分析

3.1 算例

一平板结构如图4所示,两侧固定,原始设计域为100mm×50mm,假定材料弹性模量 E=200GPa,泊松比为 ν=0.3,体积系数 f=0.5,中间施加一个集中载荷F(F=30kN)。求解时采用四节点单元,单元总数为5000,惩罚因子p=3.0,过滤半径rmin=1.5mm,阻尼系数ε=0.5,初始移动限m=0.2。求解过程中综合采用改进的优化准则算法、密度和敏度混合高斯过滤法及成员尺寸控制法。

3.2 算例分析

在第一级拓扑优化中没有施加最小尺寸约束,优化结果如图5所示,产生上下两个不规则小空洞(图5中虚线圆形区域内),这两个不规则小空洞在结构和功能上没有任何作用,但会给后续的制造和加工带来困难。因此,从制造的角度考虑,这种局部不规则小空洞的是优化设计过程中不期望获得的结构。针对两个不可制造小空洞子域,可采取最小、最大成员尺寸约束控制。图6a所示为施加最小尺寸约束后的第二级优化结果,结构中的不规则小空洞消失了,有利于后继加工制造。图6b所示为施加最大尺寸约束后的二级优化结果,同样也获得了良好的结构,满足后续的加工制造要求。在相同的基结构和载荷及边界条件下,文献[2]中的优化结果如图7所示。图7的优化结果与本文的优化结果很相似,因此也验证了本文所提出方法的可行性与有效性。

在实际优化设计过程中,具体是加入最小尺寸约束还是最大尺寸约束,要根据工程设计的实际要求或工程经验而定。这里对优化模型进行了简化,其边界条件相对简单,而在实际工程中其工况较复杂,需要考虑的因素及约束也较多,应根据不同对象要求施加不同的制造工艺约束或者多种工艺约束的组合灵活应用,充分考虑产品实际加工制造过程中的各种约束,从而使优化结果便于制造,使优化流程真正集成到产品开发过程中。

4 结束语

为提高拓扑优化结果的工程可利用程度,本文提出了面向制造的分级拓扑优化设计方法,并以实例验证了该法的可行性及有效性;建立了基于制造工艺约束的SIMP拓扑优化模型;在解决拓扑优化数值不稳定问题上,使用了一种改进的密度和敏度混合过滤算法。该算法易于实现,通用性较好。

[1]Thomas H.Applications of Topology Optimization for Weight Reduction duringPreliminary Design[C]//64th Annual International Conference on Mass Properties Engineering.Annapolis,M aryland,USA,2005:3372.

[2]左孔天.连续体结构拓扑优化理论与应用研究[D].武汉:华中科技大学,2004.

[3]Harzheim L,Graf G.TopShape:An Attempt to Create Design Proposals Including Manufacturing Constrains[J].International Journal of Vehicle Design,2002,28(4):389-409.

[4]陈义保,罗震.基于制造工艺约束的结构拓扑优化设计[J].华中科技大学学报(自然科学版),2006,34(8):77-79.

[5]Zuo Kong—Tian,Chen Li—Ping,Zhou Yunqing,et al.Manufacturing and Machining—based Topology Optimization[J].The International Journal of Advanced Manufacturing Technology,2006,27(5/6):531-536.

[6]Bendsoe M,Sigmund O.Material Interpolation Schemes in Topology Optimization[J].Archive of Applied M echanics,1999,69(9/10):635-654.

[7]Svanberg K.The Method of M oving Asymptotes–a New Method for Structural Optimization[J].International Journal for Numerical Methods in Engineering,1987,24(2):359-373.

[8]罗震,陈立平,黄玉盈,等.基于RAM P密度—刚度插值格式的结构拓扑优化[J].计算力学学报,2005,22(2):585-591.

[9]Sigmund O.Design of M aterial Structures Using Topology Optimization[D].Kongens Lyngby,Denmark:Technical University of Denmark,1994.

[10]刘震宇,王晓明,郭东明.利用窗函数解决连续体结构拓扑优化中的棋盘格式问题[J].中国机械工程,2000,11(6):705-708.

[11]Bruyneel M,Duysinx P.Note on Topology Optimization of Continuum Structures Including Self—weight[J].Structure Multidisciplinary Optimization,2005,29(4):245-256.