基于交通流灰色关联熵的交通流无序转化研究*
李 松 贺国光 张 杰
(河北大学管理学院1) 保定 071002) (天津大学系统工程研究所2) 天津 300072)
0 引 言
交通流无序是指处于交通拥堵状态下的、通行能力很低的一种道路交通流,它实质是一种在时间、空间有序,而功能无序的道路交通流.交通流系统是复杂的开放巨系统,组成系统的各因素之间存在着复杂的非线性关系,它不仅能导致交通流混沌现象的产生,也会导致交通流无序的产生.近年来,交通流混沌的研究已经受到了交通流理论界的广泛重视[1].关于交通流混沌的研究成果也越来越多[2-5].但是,对于交通流无序的研究却是交通流理论研究的一个薄弱环节.交通流无序是交通流中很常见的一种交通流形态,是不能回避的一个交通流问题.为了能够更好地对交通流实施控制,必须对交通流无序的转化过程有一个较深入的认识.
本文是在目前交通流混沌研究的基础上,通过跟驰模型模拟道路上发生交通堵塞事件产生的仿真交通流时间序列来研究了交通流无序的转化过程;提出了交通流灰色关联熵模型,并通过该转化模型对交通流无序转化过程作了分析.
1 基于跟驰模型的交通流无序转化仿真
1.1 交通流无序仿真
仿真实验选用改进的非线性跟驰模型[皮埃莱(Bierley)模型]来产生交通流的时间序列[6]
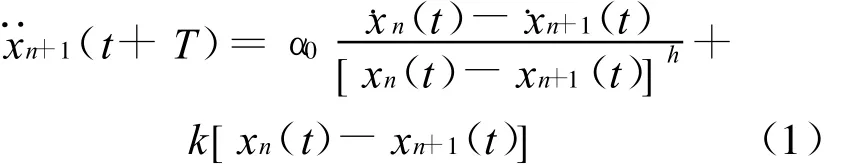
式中 :˙xn(t)为第 n 辆车(前车)速度;˙xn+1为第 n+1辆车(后车)的速度;α0为反应灵敏度系数,m/s;α0/[xn(t)-xn+1(t)]h为灵敏度的度量,其中h为常数;¨xn+1(t+T)为下一采样时刻的n+1辆车的加速度;k为相对车头间距的灵敏系数;xn(t)-xn+1(t)为车头间距.
实验中,假设头车以速度V0匀速运动,取模型参数h=1、初始速度v0=15 m/s、初始车头间距L0=15m;正弦干扰信号振幅 A=1m/s,角频率ω=0.05 rad/s;同时,假设车辆在道路上行驶350 s时,突然发现前面出现交通堵塞事故,驾驶员会渐渐减速到v0=4m/s,而后匀速运动1 350 s之后,交通堵塞事故消除,驾驶员又提速到v0=15 m/s的速度,接着又以v0=15 m/s的速度匀速前行.针对不同的车辆数N、灵敏系数α0、车间距的灵敏度k产生不同的交通流序列,反复进行对比研究,从而得出该交通流模型在出现交通堵塞事故情况下产生交通流无序的规律.
图1是当 N=5,(α0,k)组合分别为(8,0.000 08)、(14,0.000 08)、(16,0.000 005)、(5,0.000 008)时的车队的第1~2辆车、第2~3辆车、第3~4辆车、第4~5辆车之间的车头间距的时间序列,分别称之为序列1、序列2、序列3、序列4.
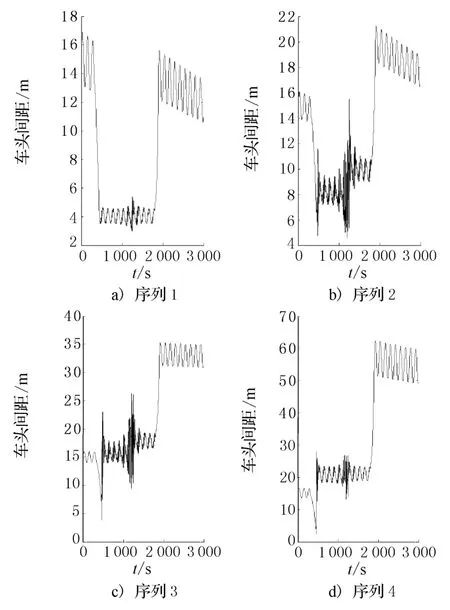
图1 N=5时不同位置车辆的车头间距时间序列
1.2 交通流无序运动特性分析
应用最大Lyapunov指数改进算法[7]计算仿真交通流时间序列的最大Lyapunov指数,结果列于表1.

表1 交通流时间序列的最大Lyapunov指数
从计算结果可以看出:5辆车之间不同的车头间距时间序列的最大Lypunov指数均为正值,表明仿真交通流处于不可预测的无序状态,存在交通流混沌.同时,序列 2和序列 3的 λ1要远远大于序列1和序列3的λ1.这说明不同位置的车辆之间的车头间距时间序列的最大Lypunov指数λ1不同,其混沌程度也不相同.
交通系统无序是以一种特殊的交通流混沌方式体现出的丧失通行能力的功能无序.交通流无序在时间、空间上依然保持着有序,它体现的是一种宏观无序而微观有序的交通流状态.因此,文中的交通流振荡现象是一种交通无序现象.其特征是[8]:车辆行驶速度低于道路设计速度的30%、混沌持续时间较长,一般在20min以上,且一般其最大Lyapunov指数λ1>0.1.
2 交通流有序运动与无序运动之间的转化
2.1 交通流有序到交通流无序的转化过程
由上述分析可以看出,在所设仿真条件下,仿真交通流产生了交通流无序现象.为进一步研究交通流从有序运动到无序运动的转化过程,图2和图3分别给出了图1b)在1~560 s时段的三维相图和二维相图.
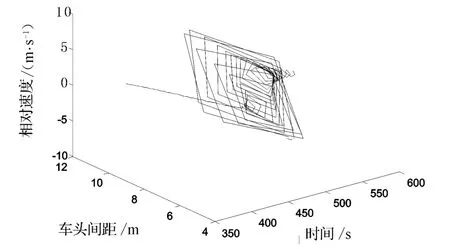
图2 仿真交通流由有序向无序转化三维相变图
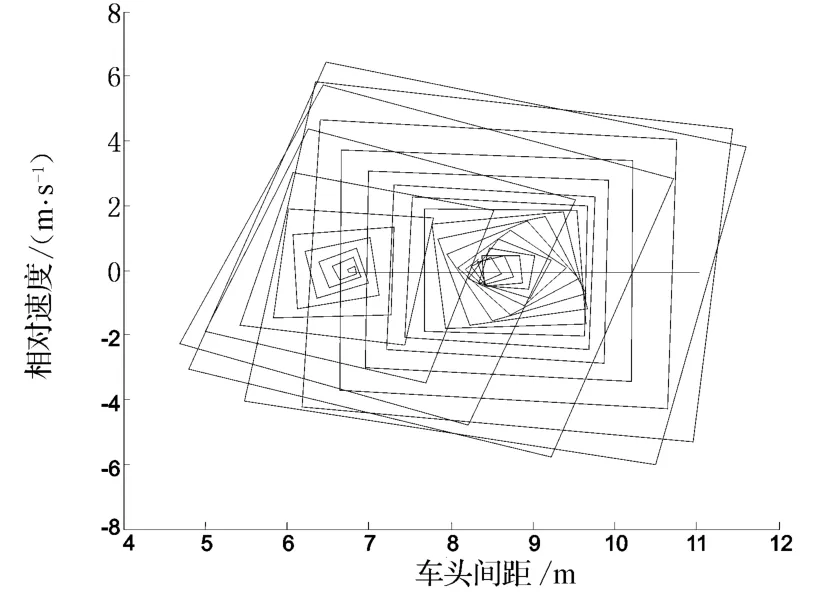
图3 仿真交通流由有序向无序转化二维相变图
从图2、图3可以看出,仿真交通流从有序运动向无序运动转化的初始阶段具有交通流混沌的明显特征(混沌吸引子在图3中清晰可见).这说明在仿真交通流从有序运动转化为无序运动的开始点——可以称之为相变临界点,是以有序运动向混沌运动转化的方式实现有序运动向无序运动的转化的,即在交通流有序向交通流无序转化的过程中存在一种过渡状态——交通流混沌.
实验中发现,交通流有序运动向无序运动转化以及交通流无序运动向有序运动转化,都发生在交通流系统的非平衡相变临界点附近,这个临界点就是实验中设定的交通堵塞事故的开始和结束.
2.2 交通流无序到交通流有序的转化过程
由图1b)和图1c)可以看出,当仿真交通流从有序运动转化为无序运动时,首先经过交通流混沌这样一个转化过渡状态,然后转化为混乱的交通流无序.这一阶段交通流可能会在自组织的作用变得有一定的规律性,但其整体仍处于一个混乱(无序)的状态.其后,由于交通流系统长时间处于无序状态,驾驶员开始变得焦躁,使交通流陷于一个更大的混乱状态,直至交通流再次变得相对规律些.如此反复,直到在非平衡相变临界点交通流无序运动转化为有序运动为止.
实验发现,在交通流无序向交通流有序转化过程中,会伴随着一些交通流混沌现象的出现,并且能够观察到混沌吸引子的存在(相图略).这也是交通流无序能够反映出交通流混沌特性的一个原因.
实验中还发现,在经过长时间的无序运动的交通流无序转化为交通流有序时,交通流无序已经变得比较平稳.这一点,从交通流无序运动转化为有序运动的相变图看得更清楚,如图4所示.由图4可以看出,当交通流无序运动转化为有序运动时,虽然车头间距的变化仍然呈比较剧烈的震荡状态,但它已经变得相对有规律得多.
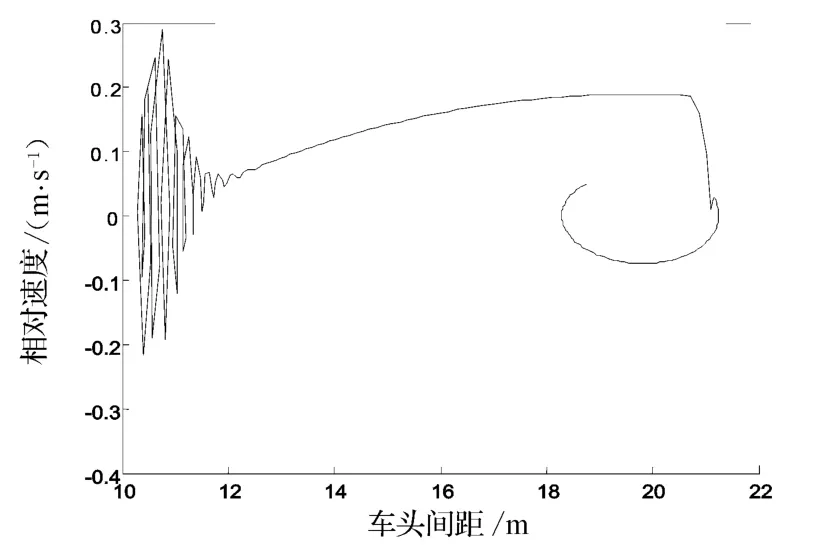
图4 仿真交通流由无序向有序转化相变图
3 基于灰色关联熵的交通流无序转化分析
3.1 交通流灰色关联系数
根据灰色系统理论[9],设
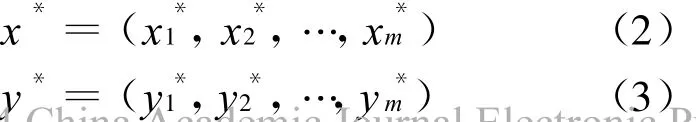
式中:xi*为某条路t时段的实际道路通行能力序列,xi*(1≤i≤≤m)为给定该条路中第i个路段的实际道路通行能力;yi*为保持道路畅通t时段该条路的最大允许道路通行能力序列;yi*(1≤i≤m)为给定该路第i个路段的最大允许道路通行能力.

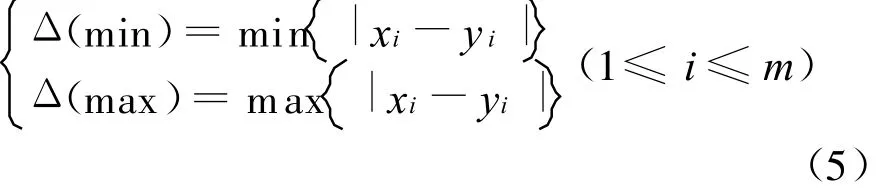
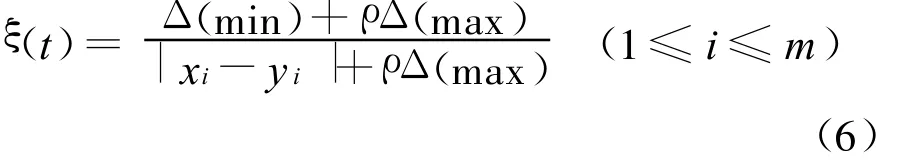
式中:ρ(0<ρ<1)为分辨系数,通过设置其值,可以控制ρΔ(max)对数据转化的影响,一般取ρ=0.5时具有较高的分辨率.
3.2 交通流灰色关联熵
按照信息熵的概念作如下定义.
定义1 设序列 X=(x1,x2,…,xn),xi≥0,且=1,xilog xi为X序列的灰熵,xi为属性信息.
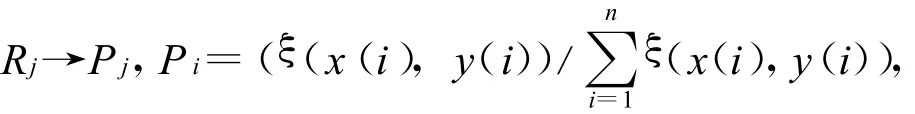
根据灰熵定义以及灰色关联系数分布映射定义,交通流灰色关联熵可以表示为
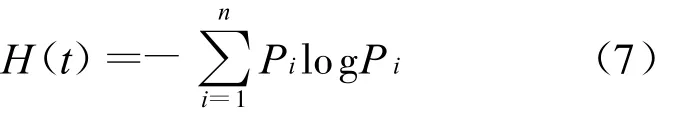
式中:H(t)为第t时段交通流系统的灰色关联熵,是道路通行能力的状态函数,当交通流系统状态一定时,其交通流灰色关联熵为确定值.
因此,交通流灰色关联熵可以作为道路交通流无序的定量度量,即:H(t)=Pi log Pi≥0时,交通流处于有序状态;H(t)=Pi log Pi<0时,交通流处于无序状态.
3.3 交通流无序的转化分析
交通流系统是一耗散结构,其转化方向取决于交通流系统运动机制,即取决于交通流系统熵变机制.因此,可以用熵理论和熵变关系作为检验和判断交通流无序转化规律的理论和方法.
式(7)仅考虑了交通流内部产生的灰色关联熵,当考虑外界环境的信息交换时,交通流灰色关联熵的完整表达式为
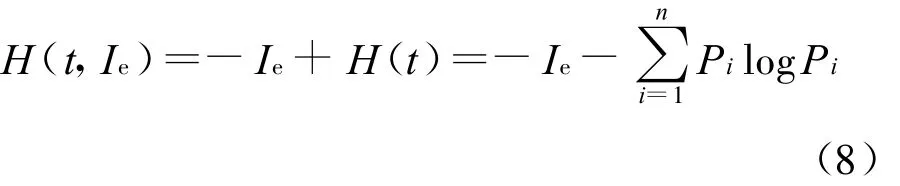
为此,建立交通流系统转化方向的判别模型
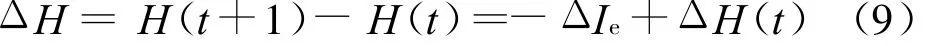
式中:ΔH为t时段系统与外界物能交换引起的熵变值;H(t+1)为系统第t时段的末态熵;H(t)为第t时段的初态熵;ΔI e=I e(t+1)-I e(t)为环境输入的信息,即负熵流;ΔH(t)为系统不可逆交通流灰色关联熵增加值,这个量总是正值.
根据交通流灰色关联熵的熵变值ΔH的大小,可判断交通流系统转化方向和内部稳定程度:(1)当ΔH>0时,交通流系统总熵增加,无序度加大,系统结构失稳,交通流系统处于不稳定状态的恶性循环过程中,这时要通过某种措施加以调控.(2)当ΔH<0时,即系统靠近熵产生最小的状态,系统总熵减小,有序度增强,表明交通流系统处于良性循环状态和过程之中,系统功能最佳.(3)当ΔH=0时,说明一定时间间隔内交通流灰色关联熵的熵变值无变化,表明交通流系统状态没有变化.
因此,当 H(t)=- Pilog Pi≥0,即交通流处于无序状态时,除了交通流的自组织及优化交通流序参量之外,还需要向交通流输入外界信息,即负熵流,从而在一定程度上消减无序,帮助交通流实现有效的自组织,使其保持并恢复有序状态.一般可将式(8)中I e的改变和控制称为“交通流诱导管控策略”.此时,若要交通流无序转化为交通流有序 ,则要:ΔI e>0,且 ΔIe>∣ΔH(t)∣,才有ΔH<0,即在不违反热力学第二定律的条件下,远离平衡的非线性系统可以通过负熵流来减少总熵,从而使系统从无序态变为有序态.
反之,当交通流处于有序状态时,即:H(t)<0,此时,若 ,ΔIe<0 且∣ΔIe∣≥∣ΔH(t)∣,则交通流有序就可能会转化为交通流无序.
一个远离热平衡的开放系统要想从无序状态转变为有序状态,就必须从外界获得信息(负熵).这是自组织理论导出的基本结论.所以,在实际交通流中,除了交通流序参量的优化之外,还需要向交通流输入外界信息,即负熵流,从而在一定程度上消减无序,帮助交通流实现有效的自组织,使其保持并恢复有序状态.
4 结 束 语
本文利用跟驰模型产生的仿真交通流研究了交通流有序运动与无序运动之间的转化过程;提出了基于交通流灰色关联熵的交通流无序转化模型,并通过该模型对交通流无序转化过程作了分析.从仿真结果及其分析可以得出如下结论:交通流无序是一种复杂的交通流状态,其转化过程是复杂多变的,且转化过程中存在交通流混沌现象;交通流系统要从无序运动转化为有序运动必须要从外界获得负熵流——信息熵.
[1]王东山,贺国光.交通流混沌研究综述[J].土木工程学报,2003(1):68-73.
[2]Low D J,Addisonp S.Chaos in car-fo llowingmodel w ith a desired headw ay time[C].Proceeding of the 30thISATA Conference,Florence,Italy,1997,175-182.
[3]冯蔚东.基于自组织理论的交通流及其管控研究[D].天津:天津大学系统工程研究所,1998.
[4]张智勇,荣 建,任福田.跟驰车队中的混沌现象研究[J].土木工程学报,2001(1):58-59.
[5]贺国光,万兴义,王东山.基于跟驰模型的交通流混沌研究[J].系统工程,2003(2):50-55.
[6]丹尼尔·L·鸠洛夫,马休·J·休伯.交通流理论[M].蒋 璜,译.北京:人民交通出版社,1983.
[7]李 松,贺国光.基于最大Lyapunov指数改进算法的交通流混沌判别[J].武汉理工大学学报:交通科学与工程版,2006,30(5):747-750.
[8]李 松,贺国光,张晓利.一种基于交通熵的交通流无序度量方法[J].公路交通科技,2007(11):92-95.
[9]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990.

