以Guglielmi模型研究脉冲电流下Ni–SiC复合电沉积

胡飞，吴坚强，黄敏，江毅

（景德镇陶瓷学院，江西 景德镇 333001）

【电镀】

以Guglielmi模型研究脉冲电流下Ni–SiC复合电沉积

胡飞*，吴坚强，黄敏，江毅

（景德镇陶瓷学院，江西 景德镇 333001）

在Guglielmi模型的基础上，推导了采用方形、上三角形、下三角形和锲形四类脉冲波形复合电沉积时，电流与镀层中惰性微粒体积分数的数学关系，并以Ni–SiC复合电沉积为例，进行了试验验证。结果表明，在相同峰值电流密度下，方波脉冲电流下SiC的沉积量是其他三类脉冲电流波形的1.51倍；而当平均电流密度相同时，方波脉冲电流下SiC的沉积量是其他三类电流波形的1.06倍。分析了电流密度对镍基体上SiC沉积量的影响。

镍；碳化硅；复合电沉积；脉冲电流；建模

Author’s address:School of Materials Science and Engineering, Jingdezhen Ceramic Institute, Jingdezhen 333001, China

1 前言

金属基复合材料是以基质金属为均匀连续相，不溶性固体微粒为分散相。电沉积复合材料是在镀液中掺入不溶性微粒(如SiO2、Al2O3、SiC、WC等硬质微粒[1-3])，微粒在金属相的弥散分布能有效提高镀层材料的耐磨性能、耐蚀性能及耐高温氧化性能等。因此，复合镀技术在表面工程领域发挥着重要作用。其中，Ni–SiC复合材料因其在微机械系统和航空航天工业上表现出的优异性能，而成为近年来的研究热点。SiC微粒的直径可以大于1 cm，也可以小于1 µm。研究表明，纳米级SiC微粒与基体有较好的结合力[4-6]。尽管电镀的工艺参数与镀层的性能之间有着密切相关，如加入Na3Co(NO2)6等添加剂可以显著提高镀层中SiC微粒的体积含量[7]，但是较少文献报道脉冲电流对镀层中SiC微粒含量的影响。电沉积复合镀层的理论很多[7-10]。Guglielmi提出了经典的两步法微粒吸附沉积理论，其模型给出了微粒沉积量与电流密度及镀液中微粒体积含量的关系。Guglielmi模型已被用于Ni–SiC复合电沉积研究，Wang等进一步证明了该模型也适用于纳米SiC微粒[11-12]。本文在Guglielmi模型的基础上，推导了不同脉冲电流波形下惰性微粒SiC在金属镍基体上的沉积量计算公式。

2 建立模型

Guglielmi模型根据电荷吸附的理论来研究复合沉积行为，给出了惰性微粒沉积量与电流密度及镀液中惰性微粒含量的关系式。在模型中，电荷的吸附量通过Zeta电位测定。惰性微粒在电镀液中被镍离子吸附[11-13]，形成较大的带电微粒。带电微粒以及镍离子经过两个连续的吸附步骤在阴极形成薄膜：第一步，溶液中的带电微粒及镍离子通过机械搅拌到达 Helmholtz双电层表面，此时微粒与电极表面的吸附力较弱；第二步，带电微粒受到电泳吸引力的作用而进入阴极表面，在库仑力作用下，带电微粒及镍离子在电极表面形成较强的吸附而形成沉积层。根据Langmuir吸附理论和法拉第定律，Guglielmi推导出下列的复合沉积方程：

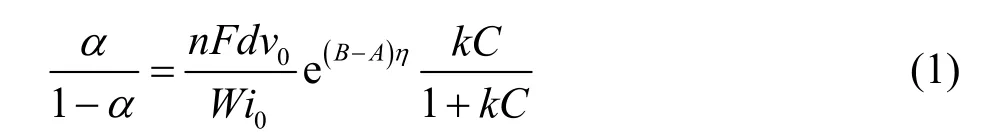
其中电流与电位的关系可用 Tafel公式转换，即i i0≈ eAη。因此，式(2)又可以写成：

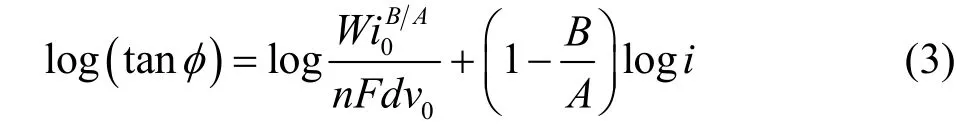
式(1) ～ (3)中：α为镀层中微粒的体积分数(%)；W、i0、n、F、d、A和i是金属的电沉积参数，其中W是金属的原子量(镍为58.69)，n是镀层金属的离子价态(镍为2)，F为法拉第常数(96 500 C/mol)，d为镀层的密度(g/cm3)，A为塔菲尔常数，i0为交换电流密度(A/cm2)，i为外加电流密度(A/cm2)；B和k是微粒沉积的参数，对于SiC微粒而言，1/k = 0.12，B = 1.51A[10]；v0则是惰性带电微粒的还原速度，它决定了微粒的沉积量。

2. 1 脉冲电流波形

图1是实验所用的4种脉冲电流波形，分别为方形(Irec)、上三角形(Irup)、下三角形(Irdn)和锲形(Itri)。脉冲周期 T=ton+toff，其中ton为导通时间，toff为关断时间。脉冲电流波形可以表示为关于时间的函数：

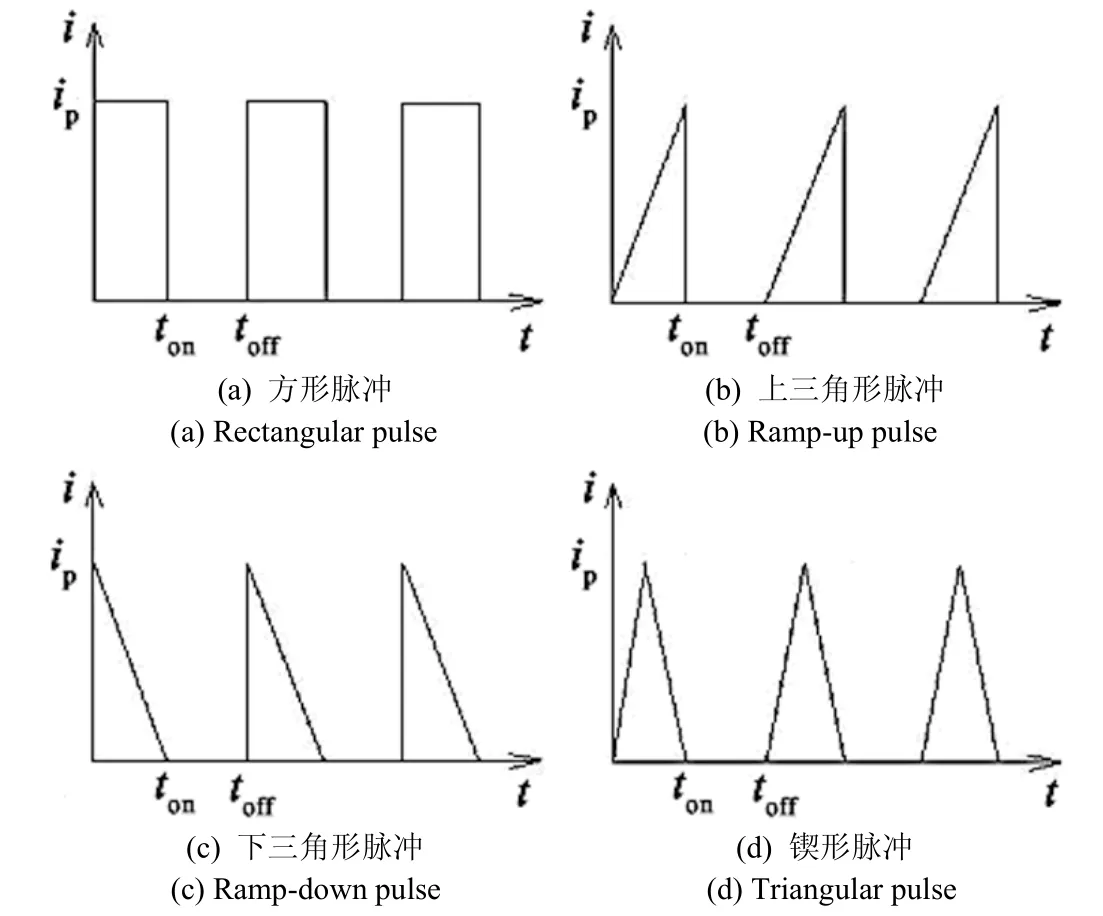
图1 脉冲电流波形Figure 1 Different types of pulse current waveform

经傅立叶级数变换后，脉冲波形可用单一方程式表示为式(5) ～ (8)，其中m表示占空比，n是傅立叶函数级数转换引入的变量(n = 1，2，3……)。

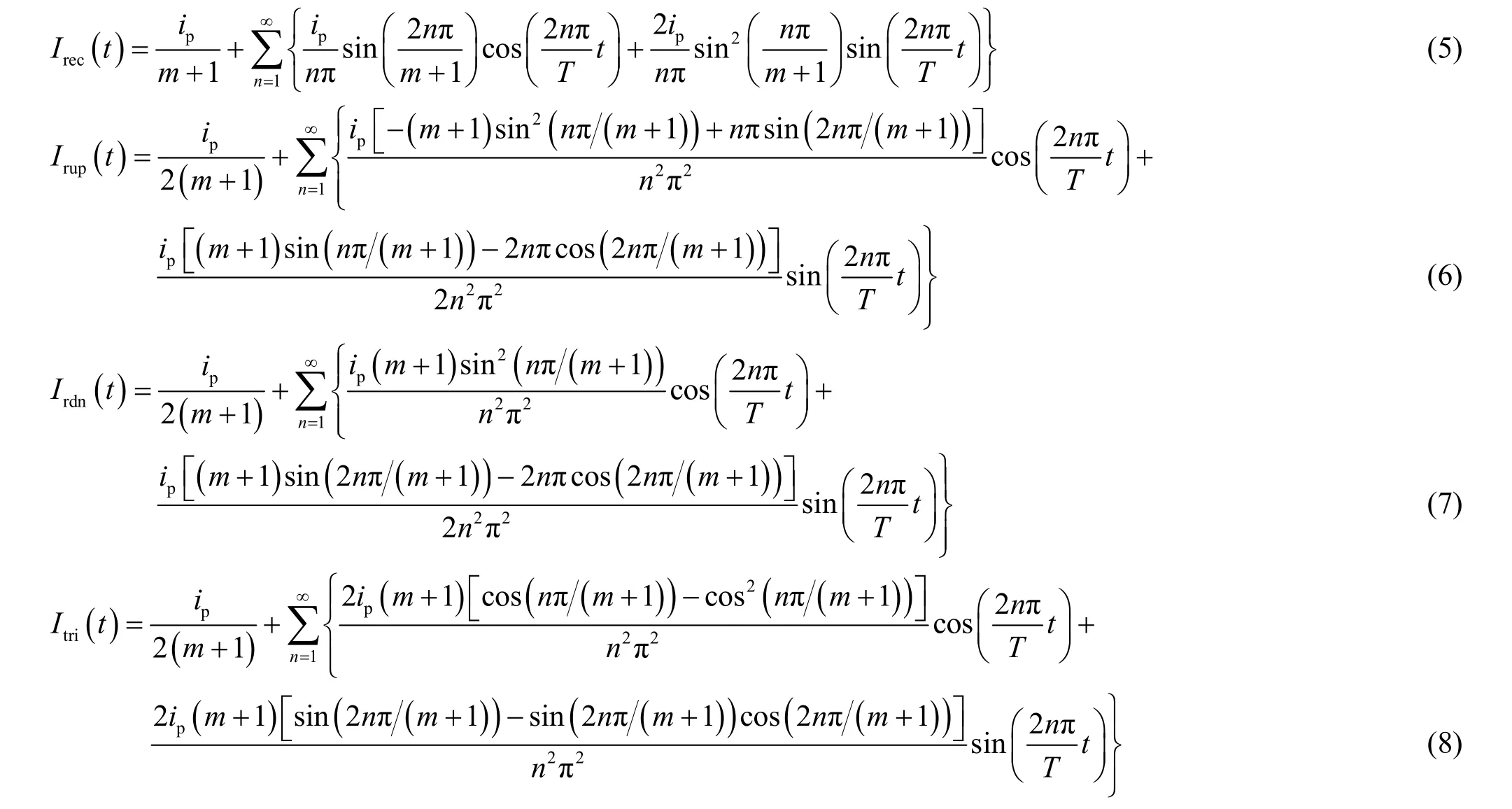
图2是峰值电流密度ip= 5 A/dm2时的电流波形傅立叶函数图形(周期0.1 s，占空比50%)。

2. 2 微粒沉积量的模拟

式(3)是关于直流电源与镀层微粒复合量的关系。为了得到任意电流波形与镀层微粒复合量的数学计算式，将脉冲电流波形划分为无限小的直流(如图 3所示)，在每个小直流电源的作用下，惰性微粒的复合量按照 Guglielmi模型计算，其中电流i1、i2和i3分别对应时间段t = 0 ～t1、t =t1～t2和t =t2～t3内镀层微粒复合量1α、2α和3α，并由此类推。

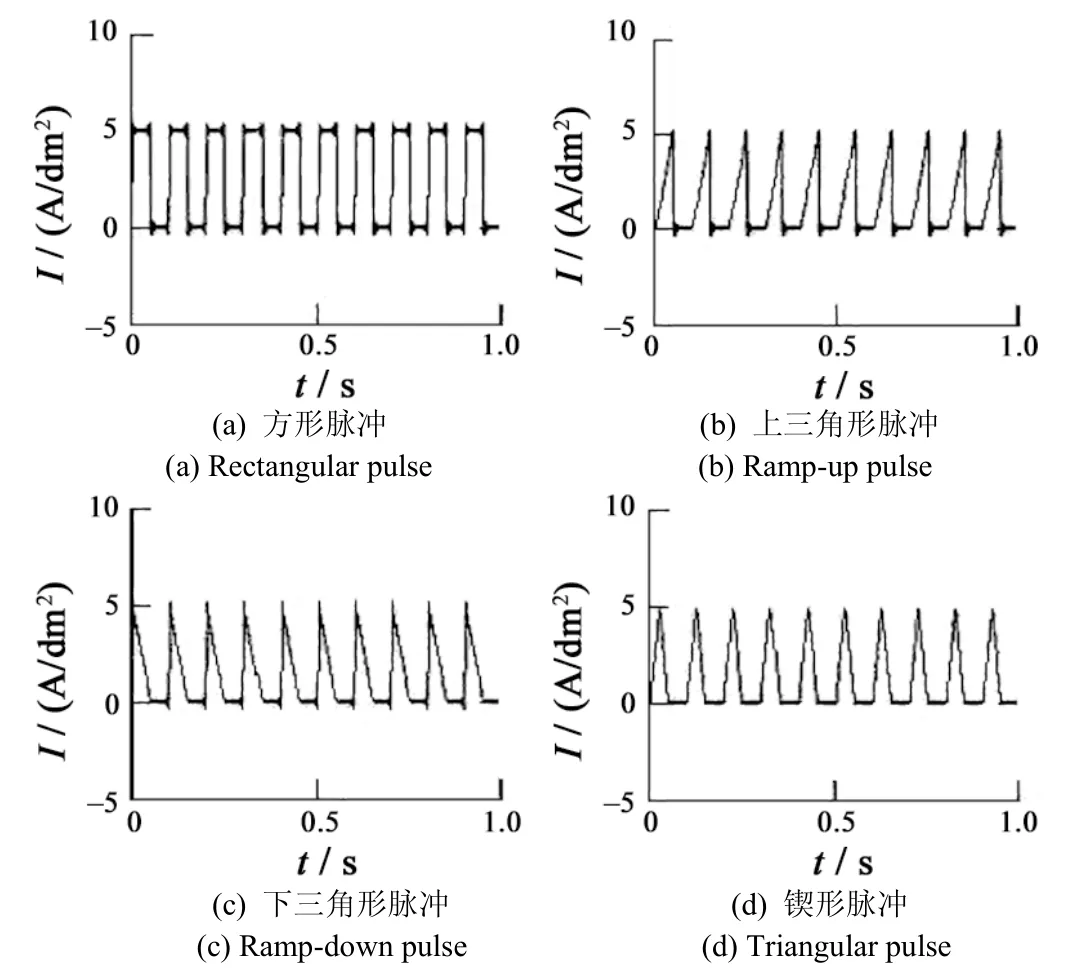
图2 峰值电流密度为5 A/dm2时脉冲电流波形的傅立叶函数图形Figure 2 Fourier series simulation of different pulse waveforms at a peak current density of 5 A/dm2

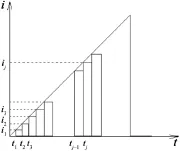
图3 上三角电流波形的积分示意图Figure 3 Schematic diagram of integration of ramp-up pulse

在任一时间段tj−1＜ t＜ tj中，惰性微粒SiC在基体镍中的体积分数可以表示为：

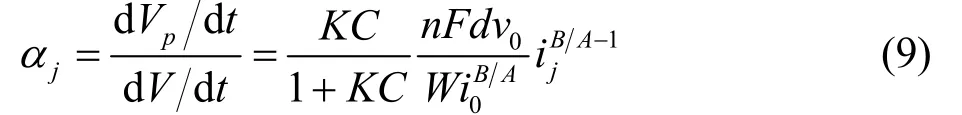
由式(9)可以看出，惰性微粒SiC复合的体积分数随着电流密度的增加而增加。当施以电流波形时，将无限多个小区间的直流用积分法计算出微粒复合量。由于脉冲关断期间没有电流通过阴极，假定电镀过程受到电荷转移的控制，忽略关断时间对传质的影响，那么在一个电流周期内无限多个直流电流对镀层中SiC体积分数的总和可以表示为：

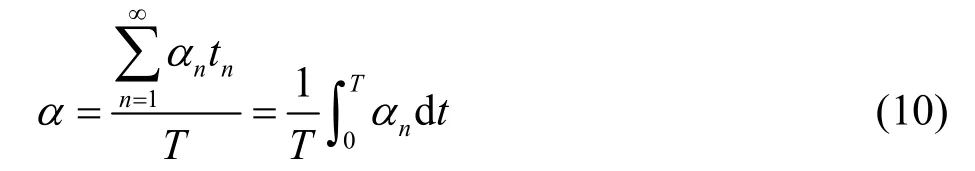
将不同脉冲波形的电流函数表达式I(t)代入式(10)，则在任意时间段t内，镀层中惰性微粒SiC的体积分数可以表达为：

通过比较不同电流波形所产生的镀层微粒复合量可以发现，在相同的峰值电流密度下，上三角形、下三角形、锲形脉冲电流下所得镀层的惰性微粒 SiC复合量相同，而方形脉冲电流具有较大的镀层微粒复合量。上三角形和方形脉冲电流下镀层微粒复合量之比为：

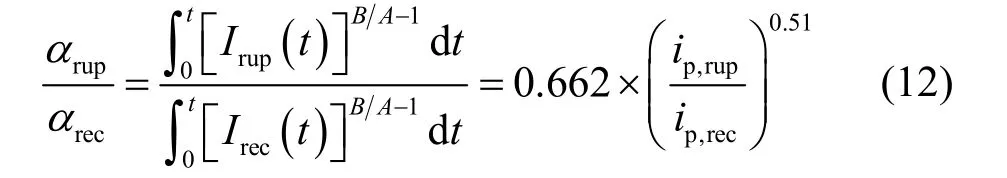
3 实验

电镀液用蒸馏水配制，其组成如下：氨基磺酸镍330 g/L，氯化镍15 g/L，硼酸30 g/L。在镀液中加入20 g/L β–SiC，其平均粒径为100 nm。阳极为高纯度镍板，以不锈钢为基体。采用水浴加热控制镀液温度为50 °C，镀液pH为4.2。电镀前超声分散2 h，磁力慢速搅拌使微粒悬浮。惰性微粒 SiC的体积分数通过阿基米德法测得[14]。

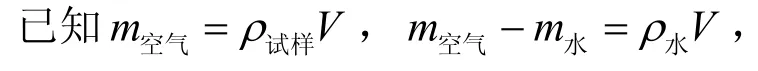
其中V是试样的体积(m3)，m空气和m水分别表示试样在空气和水环境中测得的质量(g)，ρ试样和ρ水分别为试样和水的密度。则

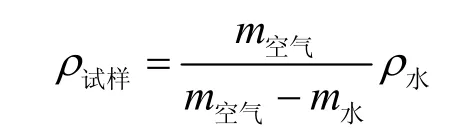
镀层中SiC的体积分数α可以根据ρ试样通过式(13)求出：

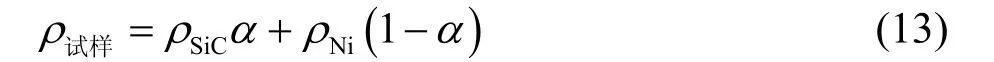
其中镍的密度ρNi= 8.902 g/cm3，SiC的密度ρSiC= 3.217 g/cm3。

4 结果与讨论

图4为4种脉冲电流波形制备的Ni–SiC复合镀层中SiC微粒的体积分数随电流密度的变化曲线。从图4可以看到，随着电流密度的增大，镀层中SiC微粒的体积分数不断增加。但当电流密度大于5 A/dm2时，SiC微粒体积分数的增加幅度减小。从图 4还可看出，方形脉冲电流下所得复合镀层中 SiC微粒的体积分数最高，其余3种脉冲电流波形下镀层中SiC微粒的体积分数相近。

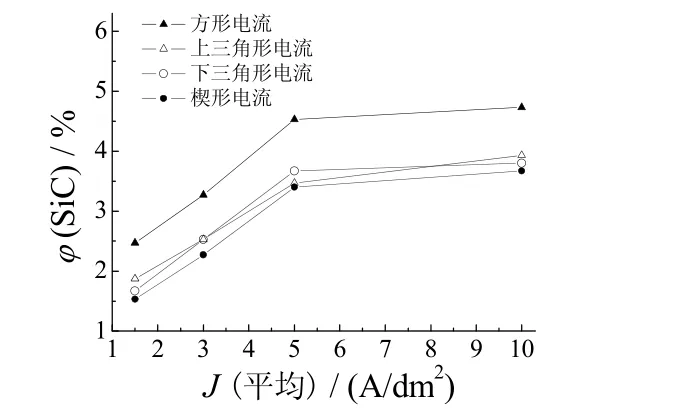
图4 4种脉冲电流波形下镀层中SiC微粒的体积分数Figure 4 Volume fractions of SiC particles in deposits prepared under different pulse current waveforms

图 5 为 Guglielmi模型计算出的不同脉冲电流波形下所得镀层中SiC微粒的体积分数。从模拟结果可以看出，SiC微粒的体积分数在不同电流波形下随着电流密度的增大而增加，并且方形电流下所得镀层的SiC微粒含量最高，而其他 3种电流波形下所得镀层具有相同的SiC微粒含量。模拟结果与图4的实验结果吻合，在较低电流密度下，镀层中SiC微粒体积分数的增加速率(以斜率αip表示)较高，而此斜率随着电流密度的增大而逐渐降低，这也与上述的实验结果吻合。

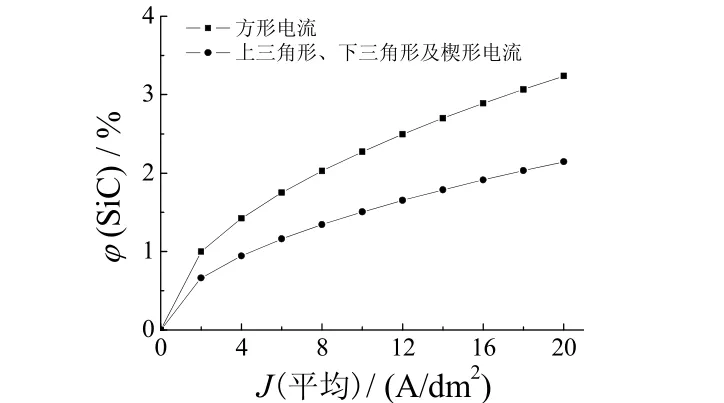
图5 模拟脉冲电流波形下镀层中SiC微粒的体积分数Figure 5 Predicted volume fractions of SiC particles in deposits prepared under different waveforms

电流密度对微粒复合量的影响非常复杂。在某些体系中，随着电流密度的增大，微粒复合量会持续增加，如Ni–TiO2[15]和Ni–P–SiC[16]体系；微粒复合量也可能随电流密度增大而减小，如 Ni–金刚石[17]和Cu–MoSi2[18]体系；某些体系中，微粒复合量会在某一电流密度下达到最大，如ZnNi–SiC[19]体系；也有的体系会在某一电流密度下达到最小的微粒复合量，如Cr–Al2O3[20]体系。

一般认为，微粒复合沉积量受到电荷转移及物质传递的控制：在较低电流密度下，微粒复合过程由电荷转移控制，此时微粒的含量随着电流密度的增大而增加；当电流密度较高时，微粒复合受到物质传递的控制，出现微粒复合量随电流密度增大而下降的趋势。也有研究认为，微粒和金属的沉积受到两种不同因素的控制：微粒的沉积通过机械搅拌传质，因此受物质的传递控制；金属的沉积则受电荷的转移控制。在低电流密度下，金属的电荷转移量小，而微粒的传质快，因此低电流密度下的微粒复合量高。

在本文的模型中，微粒被镍离子吸附而形成带电离子，受电泳吸引力而吸附在阴极表面，其吸附量按照Langmuir吸附理论计算。因此镀液中微粒及离子的传质对微粒复合量有非常重要的影响。当镀液中微粒的传质速度小于电荷的转移速度(即电流密度较高时)，镀层中微粒复合量会降低。试验结果表明，电流密度为5 A/dm2时的微粒复合量与电流密度为10 A/dm2时的微粒复合量相近，说明当电流密度大于5 A/dm2时，电流密度对微粒复合量的影响较小。镀层中SiC微粒含量不随电流密度的增大而降低，可能与脉冲关断期内阴极表面微粒及离子的传质补充有关。传质的补充可使电荷的转移充分进行，微粒的复合没有受到物质传递因素的控制，故并未出现微粒复合量随电流密度增大而下降的趋势。文中的模型没有考虑物质的传质对微粒复合量的影响，得到的是理想化的电荷转移控制下微粒复合量的变化情况，因此在高电流密度下，模拟结果与实验结果有差距。

5 结论

研究了脉冲电流波形下Ni–SiC复合材料的电沉积行为。在Guglielmi模型的基础上，推导了脉冲电流波形沉积下镀层中SiC体积分数的计算公式，模拟的结果与实验结果相近。在所研究的 4种波形电流中，方形电流可获得最高的SiC微粒复合量。

[1] GYFTOU P, STROUMBOULI M, PAVLATOU E A, et al. Electrodeposition of Ni/SiC composites by pulse electrolysis: Electrodeposition in electronics [J]. Transactions of the Institute of Metal Finishing, 2000, 80 (3): 88-91.

[2] NOWAK P, SOCHA R P, KAISHEVA M, et al. Electrochemical investigation of the codeposition of SiC and SiO2particles with nickel [J]. Journal of Applied Electrochemistry, 2000, 30 (4): 429-437.

[3] BANOVIC S W, BARMAK K, MARDER A R. Characterization of single and discretely-stepped electro-composite coatings of nickel–alumina [J]. Journal of Materials Science, 1999, 34 (13): 3203-3211.

[4] BENEA L, BONORA P L, BORELLO A, et al. Wear corrosion properties of nano-structured SiC–nickel composite coatings obtained by electroplating [J]. Wear, 2002, 249 (10/11): 995-1003.

[5] ZIMMERMAN A F, CLARK D G, AUST K T, et al. Pulse electrodeposition of Ni–SiC nanocomposite [J]. Materials Letters, 2002, 52 (1): 85-90.

[6] ZIMMERMAN A F, PALUMBO G, AUST K T, et al. Mechanical properties of nickel silicon carbide nanocomposites [J]. Materials Science and Engineering A, 2002, 328 (1/2): 137-146.

[7] HOVESTAD A, JANSSEN L J J. Electrochemical codeposition of inert particles in a metallic matrix [J]. Journal of Applied Electrochemistry, 1995, 25 (6): 519-527.

[8] FRANSAER J, CELIS J P, ROOS J R. Mechanisms of composite electroplating [J]. Metal Finishing, 1993, 91 (6): 97-100.

[9] KIM S K, YOO H J. Formation of bilayer Ni–SiC composite coatings by electrodeposition [J]. Surface and Coatings Technology, 1998, 108/109: 564-569.

[10] MAURIN G, LAVANANT A. Electrodeposition of nickel/silicon carbide composite coatings on a rotating disc electrode [J]. Journal of Applied Electrochemistry, 1995, 25 (12): 1113-1121.

[11] GUGLIELMI N. Kinetics of the deposition of inert particles from electrolytic baths [J]. Journal of the Electrochemical Society, 1972, 119 (8): 1009-1012.

[12] CELIS J P, ROOS J R, BUELENS C. A mathematical model for the electrolytic codeposition of particles with a metallic matrix [J]. Journal of the Electrochemical Society, 1987, 134 (6): 1402-1408.

[13] LEE C C, WAN C C. A study of the composite electrodeposition of copper with alumina powder [J]. Journal of the Electrochemical Society, 1978, 135 (8): 1930-1933.

[14] SHAO I, VEREECKEN P M, CHIEN C L, et al. Synthesis and characterization of particle-reinforced Ni/Al2O3nanocomposites [J]. Journal of Materials Research, 2002, 17 (6): 1412-1418.

[15] STOJAK J L, TALBOT J B. Investigation of electrocodeposition using a rotating cylinder electrode [J]. Journal of the Electrochemical Society, 1999, 146 (12): 4504-4513.

[16] CHENG D H, XU W Y, HUA L Q, et al. Electrochemical preparation and mechanical properties of amorphous nickel–SiC composites [J]. Plating and Surface Finishing, 1998, 85 (2): 61-64.

[17] LEE E C, CHOI J W. A study on the mechanism of formation of electrocodeposited Ni–diamond coatings [J]. Surface and Coatings Technology, 2001, 148 (2/3): 234-240.

[18] WAN Y Z, WANG Y L, TAO H M, et al. Preparation and characterization of Cu–MoSi2composite coatings [J]. Transactions of the Institute of Metal Finishing, 1999,77 (1): 52-54.

[19] MÜLLER C, SARRET M, BENBALLA M. ZnNi/SiC composites obtained from an alkaline bath [J]. Surface and Coatings Technology, 2003, 162 (1): 49-53.

[20] BENEA L. Electrodeposition of zirconia particles in a copper matrix [J]. Materials and Manufacturing Processes, 1999, 14 (2): 231-242.

Study on pulse current electrocodeposition of Ni–SiC composite based on Guglielmi’s model //

HU Fei*, WU Jian-qiang, HUANG Min, JIANG Yi

The mathematical relationship between the volume fraction of inert particles in deposit and the current applied with rectangular, ramp-up, ramp-down and triangular waveforms in pulsed composite electrodeposition was derived from Guglielmi’s model, and then validated taking Ni–SiC composite electrodeposition as an example. The results showed that the amount of SiC deposited with rectangular pulse is 1.51 times that deposited with other three waveforms at the same peak current density, but is 1.06 times that deposited with other three waveforms at the same average current density. The effect of current density on the amount of SiC embedded in Ni matrix was analyzed.

nickel; silicon carbide; composite electrodeposition; pulse current; modeling

TQ153.12

A

1004 – 227X (2010) 01 – 0001 – 05

2009–03–26

2009–06–28

景德镇陶瓷学院博士启动经费；景德镇市科技局项目；江西省教育厅项目（GJJ09531）；江西省科技支撑项目。

胡飞（1978–），女，江西吉安人，博士，副教授，主要从事功能材料的研究。

(E-mail) mfhufei@126.com。

[ 编辑：温靖邦 ]