TGS单晶电畴运动的微分回线谱分析

刘俊刁,何婉芬,罗劲明,沈韩

(1.惠州学院 电子科学系,广东 惠州 516007;2.中山大学 物理科学与工程技术学院,广东 广州 510275)

铁电电滞回线是铁电体在外加电场作用下电畴反转运动的表现.但回线的测量常受到漏电电导、顺电电容、电极和样品表面接触层pn结等非铁电性的影响[1],事实上单个电滞回线一般是不闭合的[2],故不能由此精确定出铁电参数.

利用微分电滞回线谱分析方法可以克服上述问题,将多种非铁电效应从总效应中定量扣除而得到纯铁电性的贡献.曾用该方法将钛酸钡(BST)晶体中a畴和c畴的运动信号分开[3],并可用来表征锆钛酸铅(PZT)陶瓷的极化疲劳和损伤效应[4].本文中采用微分回线谱分析方法研究硫酸三甘肽(TGS)单晶的铁电畴运动.

1 微分电滞回线谱分析

TGS单晶样品厚l=0.50 mm,面积S=43.0 mm2,两面溅射Au电极.测量前先将样品两电极短路加热至62 ℃的顺电相,保温0.5 h去极化,再保持电极短路冷却至室温铁电相进行测量.

将周期为τ,峰值为±Um的三角波电压U(t)直接加于样品上,流过样品的电流I(t)用精度为0.1 pA的补偿式微电流计测出,其电压输出端口的电压值与电流成正比.可用数字存储示波器记录I随U变化的关系.I(t)可表示为

I=Iσ+Ip+IF

(1)

其中Iσ是电导的贡献,IP是非铁电性电容CP的贡献,

(2)

扣除Iσ和IP后得到的纯铁电电流IF可表示为

(3～5)

其中,QF为铁电电荷,Q0为可供激发的铁电屏蔽电荷的总量,g(U)为激发dQF所需跨越位垒的归一化分布函数[5].g(U)描述了铁电体内畴结构运动的性质,U0为峰值位置,Δ为半高半宽.三角波电压的(dU/dt)为常数,故式(3)中IF曲线和(dQF/dU)曲线的形状是完全一样的,与g(U)曲线也只相差一个系数Q0,称(Q0,U0,Δ)为微分谱参数,可用来表征铁电性.

2 实验结果及讨论

2.1畴运动随外加电压周期的变化测量了TGS单晶在峰值电压Um=±120V而周期τ不同的三角波电压作用下的微分回线.由于TGS单晶的矫顽场小于2kV/cm[6],故120V已大于样品的矫顽电压.图1套图示出了τ=5s时微分回线的一个例子,图中只画出了U≥0的正半支.实验表明,τ≥0.5s时所有回线均可用一个高斯函数精确拟合.如图1套图中的黑线所示,拟合曲线与实验点符合得很好.解谱得到的微分回线谱参数(Q0,U0,Δ)反映了畴结构的运动,其随τ的变化示于图1,可分别拟合为：

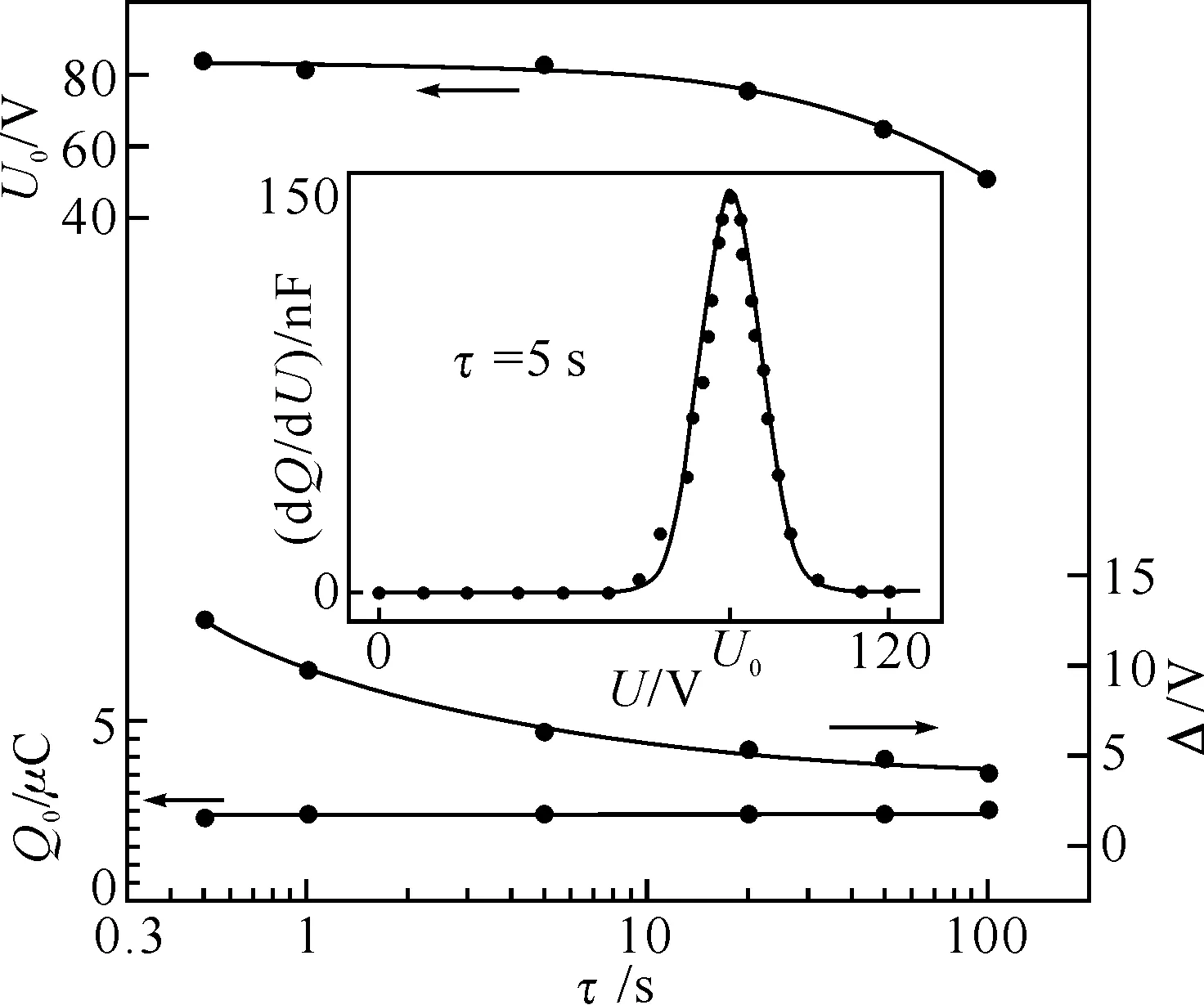
图1 TGS晶体微分回线谱参数

(6)

由此可得TGS晶体的自发极化强度Ps=Q0/2S=2.79μC/cm2,与公认值 相一致[6].当τ变小时,U0和Δ增大,表明此时需要更强的外加电场才能使电畴反转[7].当τ很小时,U0趋于稳定,Δ变得很大.当τ很大时,Δ趋于稳定,U0变小.即随外加电场频率的升高,测得的表观矫顽场逐渐增大至趋于稳定,相应地电滞回线变得越来越扁平.

图2示出了在峰值电压Um=±120V,周期τ较短的三角波作用下的一组微分回线.图中正负支曲线不完全对称,表明该样品两面的表面结构不完全相同.根据铁电极化子动力学模型[8],由于电畴的反转和生长需要一定的时间,故随着外加三角波电压的周期τ持续变小,电畴运动跟不上外电场的变化速度,铁电屏蔽电荷来不及被完全激发,微分回线逐渐偏离高斯线型,高斯函数位垒分布失去意义.但此时仍可以扣除I(U)曲线中的非铁电成分后积分得到QF(U)纯铁电电滞回线.

2.2畴运动随外加电压峰值的变化三角波电压周期固定为τ=20s,改变峰值电压Um测得的一组微分回线示于图3,图中只画出了回线U≥0的正半支.当Um足够大时,微分回线是高斯型的.随着Um的减小,由于晶体表面受潮老化、切割等原因造成的缺陷紧紧束缚住表面屏蔽电荷,这些电荷产生的电场抵消了一部分外场的作用,使得电压较小时不足以激发所有的屏蔽电荷,晶体将不能实现单畴化的完全反转,故微分回线表现为不完整的高斯曲线,电流峰值减小,峰值位置U0变小,宽度Δ变大.即随外加电场峰值的减小,测得的表观矫顽场逐渐减小,对应积分得到的电滞回线不断收缩变扁.在BaTiO3陶瓷中也曾观察到这种现象[9].

图2 不同周期的微分回线

图3 不同峰值电压下的微分回线

在三角波周期τ≥20s,峰值电压Um≥60V的情况下,TGS单晶电畴的生长完全跟得上外电压的速度,故电压增大到Um后逐渐减小至零的过程中都有I≤0,电畴立刻停止生长或反向生长,如图3中Um=60V和80V的曲线所示.但在τ很小(如小于0.5s)时,电畴生长跟不上外电压变化的速度,U从Um开始减小的初期仍有I>0,如图2所示；在τ足够大但Um较小(如小于50V)时也会出现类似的情形,如图3中Um=40V和50V的曲线所示.

3 结论

利用微分电滞回线谱测量可以得到畴运动的许多信息.只要外加电场的半周期大于电畴反转所需的临界时间,峰值电压大于完全激发所需的临界电压,就能把晶体的铁电性质与高斯函数的个数,峰位,峰高,峰宽等微观参数联系起来,从而可以替代电滞回线而成为研究铁电性质的一种新的有力手段.在不清楚被测样品微分回线谱参数的情况下,无限制地提高电滞回线的测量频率是没有意义的.

参考文献：

[1] 殷之文.电介质物理学[M].第二版.北京:科学出版社,2003:604-606.

[2] Tagantsev A K,Stolichnov I, Colla E L, et al. Polarization fatigue in ferroelectric films [J].J Appl Phys,2001,90(3):1387-1402.

[3] 李景德,沈韩,陈敏.电介质理论[M].北京:科学出版社,2003:303-306.

[4] 朱贵文,周伟华,沈韩,等.铁电体的极化疲劳和历史记忆效应[J].中山大学学报:自然科学版,2005,44(4):40-42.

[5] 李景德,李智强,陆夏莲,等.铁电屏蔽理论[J].物理学报,2000,49(1):160-163.

[6] Lines M E , Glass A M. Principles and applications of ferroelectics and related materials [M].Oxford:Clarendon Press,1977.

[7] Merz W J. Domain formation and domain wall motions in ferroelectric BaTiO3single crystals[J].Phy Rev,1954,95(3):690-698.

[8] 李智强,陈敏,沈文彬,等.铁电极化子动力学理论[J].物理学报,2001,50(12):2477-2481.

[9] Jaffe B J, Cook W R, Jaffe H.Piezoelectric ceramics[M].New York:Academic Press, 1971.