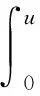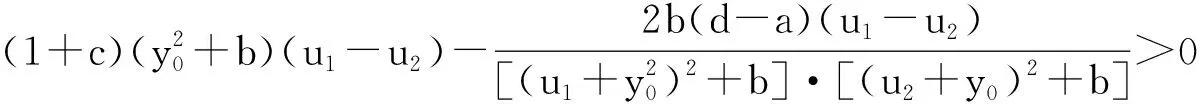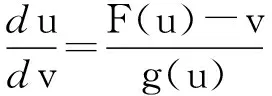一类具有二重饱和度的四分子可逆生化反应系统的定性分析

冯光庭,杨翠红

(1.湖北第二师范学院 数学与数量经济学院,湖北 武汉 430205；2.华中师范大学 数学与统计学学院,湖北 武汉 430079)

0 引言

近年来, 对生化反应系统性质的研究已取得许多好的成果.如文献[1-2]研究了具有米氏饱和反应速度的生化反应模型,文献[3]研究了具有二重饱和反应速度的生化反应模型；文献[4]研究了一类多分子生化反应系统的全局结构.但这些研究中一般只考虑了正平衡点的局部性质和极限环存在的充分条件.事实上,在对这些生化反应模型的研究中,不仅要考虑其平衡点的局部性质,还应考虑其全局性质,特别是其正平衡点全局稳定和极限环存在的充分必要条件.本文将运用文献[5-7]中的理论和方法对反应过程为

相应的数学模型为(其中a,b,c,d均为正常数)

(1)

的具有二重饱和度的四分子生化反应系统进行研究.首先确定系统(1)的正平衡点的性质,然后给出其存在唯一极限环和其正平衡点全局渐进稳定的充分必要条件.基于系统(1)的实际意义,我们只在区域Ω{(x,y)|x≥0,y≥0}内进行讨论.

作时间变换dt=(Y2+b)dτ,将系统(1)化为与之拓扑等价的系统

(2)

易知系统(2),当d≤a时,没有正平衡点；当d>a时,有唯一正平衡点M(x0,y0)其中

以下讨论均限制在d>a.

1 主要结果及证明

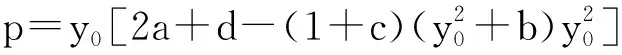
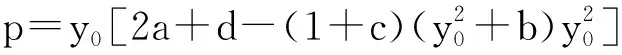
故当p>0时,M为不稳定的焦点或结点；当p<0时,M为稳定的焦点或结点.

当p=0时,为了确定M点的性质,对系统(2)作如下变换

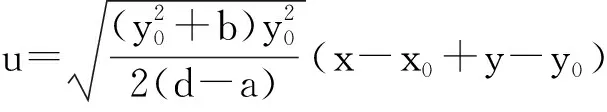
则系统(2)拓扑等价于以下系统:

(3)

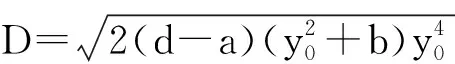
(4)

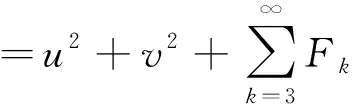
所以当p=0时,O(0,0)是系统(4)不稳定的一阶细焦点,从而当p=0时,M(x0,y0)是系统(2)的稳定的一阶细焦点.

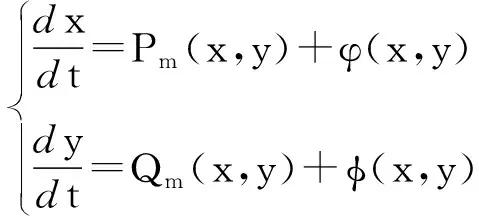
U(θ)=cosθ·Qm(cosθ,sinθ)-sinθ·Pm(cosθ,sinθ),

R(θ)=cosθ·Pm(cosθ,sinθ)+sinθ·Qm(cosθ,sinθ).

(**)

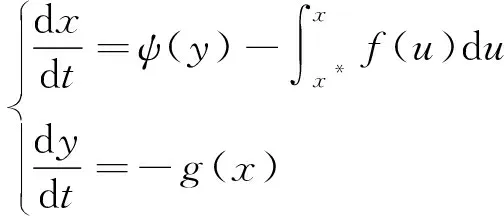
引理3 当下列条件成立时,系统(1)在区域Ω内有唯一稳定的极限环.

引理3的证明(ⅰ)存在性.

构造广义的Bendixson环域,其外境界线由L1、L2和L3构成,内境界线为平衡点M,其中L1:x轴正半轴,L2:y轴正半轴,L3:赤道线.首先考虑系统(2)的无穷远奇点.

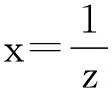
(2a)

又U(0)=0,R(0)=1>0,U′(0)=-1<0;U(π)=0,R(π)=1>0,U′(0)=-1<0.

所以由引理1知系统(2)只有一条轨线,当t→-∞时沿θ=π趋于平衡点N0(0,0);也只有一条轨线,当t→-∞时沿θ=0趋于平衡点N0(0,0).

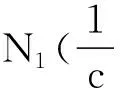
其中φ(u1,z1),φ(u1,z1)是次数不低于5次的项.

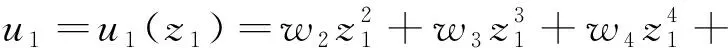
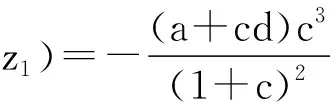
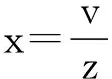
(2b)

因(0,0)不是它的奇点,故原系统沿y轴方向的无穷远点不是奇点.

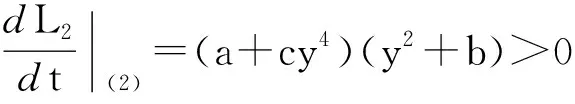
而当(Ⅰ)、(Ⅱ)成立时,有p>0,于是由定理1知,正平衡点M为系统(2)的不稳定的焦点或结点.故系统(2)在区域Ω内至少存在一个稳定的极限环,从而系统(1)在区域Ω内至少存在一个稳定的极限环.

(ⅱ)唯一性.

作变换u=y-y0,v=x+y-x0-y0,dτ=(u+y0)3dt,-y0

(5)

f(u)F′(u)=1+c-d·

再由存在性即知引理3成立.

定理2 系统(1)的正平衡点M在区域Ω内是全局渐进稳定的当且仅当条件(6)成立.

(6)

定理2的证明若M是全局渐进稳定的,则必是局部稳定,所以由定理1知p≤0.

再由p的意义即得(6)式.

故由u1>0,-y0

从而由p≤0及φ(0)=0知z>0时恒有F1(z)>F2(z).

(7)

的积分曲线.在上述Filippov变换下,系统(7)可以分为两个方程

(8)

(9)

故由定理1知,M是全局渐进稳定的.

定理3 系统(1)在区域Ω内有唯一稳定的极限环当且仅当下列条件成立.

定理3的证明由引理3知,定理的充分性成立；

由定理2知定理的必要性是显然的.事实上,当系统(1)在区域Ω内有唯一稳定的极限环时,由定理2知(Ⅱ)一定成立；

参考文献:

[1] 杨平华,徐瑞.一类生化反应系统的定性分析[J].生物数学学报,1998,13(3):361-364.

[2] 聂益民.一类可逆多分子饱和生化反应系统的非线性分析[J].生物数学学报,2005,20(1):33-36.

[3] 黄建华,张新建.一类生化反应系统极限环的存在唯一性[J].生物数学学报,2000,15(4):432-436.

[4] 严艳,杨玉华.一类生化系统的数学模型及定性分析[J].数学的实践与认识,2009,39(13):90-96.

[5] 张锦炎,冯贝叶.常微分方程几何理论与分支问题[M].北京:北京大学出版社,2003.

[6] 叶彦谦.极限环论[M].上海:上海科学技术出版社,1984.

[7] 陈兰荪,孟新柱,焦建军.生物动力学[M].北京:科学出版社,2009.

[8] 冯光庭,杨学耀,杨振兴.一个函数美妙的性质及其证明过程赏析[J].高等函授学报,2010,23(3):12-13.