基于一类2对1映射的序列的自相关性质

揣立娟

(湖北大学 数学与计算机科学学院，湖北 武汉 430062)

伪随机序列在密码学和通信等领域有着广泛的应用.周期的大小、平衡性和自相关性质是评价周期序列随机性的几个重要指标[1]，因此对具有较大周期和理想自相关性的序列的研究成为了密码学和通信学的一个重要研究领域.经过多年的努力，人们已经发现了许多理想自相关序列，如m-序列[2]，GMW序列[3]和具有梅森素数周期的勒让得序列[4]等等.利用有限域上的2对1映射构造理想自相关序列是最近提出的一种有效途径.本文中讨论了由有限域F22m上的一类2对1映射构造的二元序列的性质. 给出了这些序列的周期为2m-1且满足平衡性.基于Walsh变换技巧，本文中还证明了这些序列具有理想自相关性质.但是我们不知道它们是否为新的理想自相关序列，这个问题有待进一步研究.

1 预备知识

本节介绍了相关概念、性质及公式.

伪随机序列b={b(t)∶t∈Z},是指序列元素间有确定关系存在，但具有与随机序列类似性质的离散信号形式，可表示为…，b(-1),b(0),b(1),…,其中b(t)可取0,1;也可取有限域Fq中的元素，q为奇素数或素数的方幂.前者称为二元序列，后者称为q元序列.序列的长度可为有限，也可为无穷.人们常关注的是无穷序列中的周期序列.已知序列b={b(t)∶t∈Z},如果对任意整数t,存在一个最小的正整数N，使得b(t)=b(t+N)成立，则称N是b的周期，b为周期序列，记为b={b(t)∶t=0,1,…,N-1}.

文中的序列均为伪随机二元序列，简称二元序列.文中用到的记号有：

(1)F2n:表示含有2n个元素的有限域，其中n为正整数.n=1时，F2={0，1}；

(2)a:表示周期为N的二元序列a={a(t)∶a(t)∈F2,t=0,1,…,N-1};

(3)⊕:表示模2相加；

(4)+：表示整数相加.

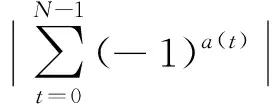
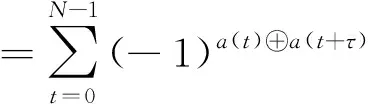
(1)

其中τ∈{0,1,…,N-1},且t+τ是模N计算的.

(2)

把具有理想自相关性质的序列称为理想自相关序列.

在第2节自相关值的计算过程中用到了迹函数的性质和Parseval等式，下面将介绍迹函数的定义、相关性质和Parseval等式.

其中x∈F2n.

Parseval等式[1]：

文中还用到的定义如下.

定义1 称φ:A→B是2对1映射，如果Imφ中任一元素有且只有两个原象，其中Imφ表示φ的象.

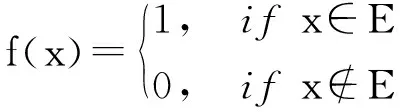
(3)

2 主要结果

这一节讨论了由有限域上一类2对1映射构造的二元序列的性质.这些序列的周期为2m-1，且具有平衡性.利用Walsh变换技巧，证明了这些序列还具有理想自相关性.

首先给出序列的构造过程.

序列构造：已知有限域F2n,n=2m,其中m为任意正整数.令q=2m,记 U={x∈F2n|xq+1=1}.

(4)

(5)

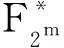
由s的构造方法知，它的周期为q-1，即2m-1.根据有限域[5]的性质，可得下面引理.

引理1 由方程(4)定义的映射是2对1的.

由引理1及序列平衡性定义，可得s是平衡的.

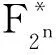
(6)

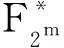
由以上引理以及Walsh变换技巧，有如下结果.

定理1 由等式(5)构造的序列s={s(αt)∶t=0,1,…,2m-2}具有理想自相关性质.

定理1的证明令f(x)∶F2n→F2是集合D=Imφ的特征函数，则

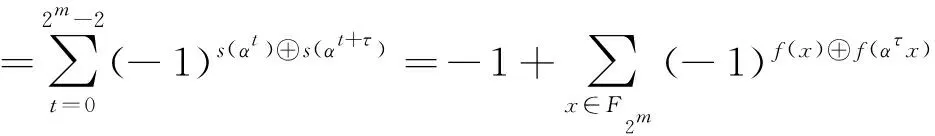
由Parseval等式有：

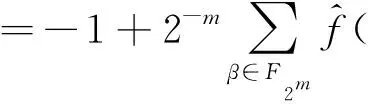
(7)

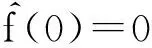
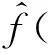
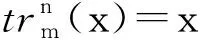
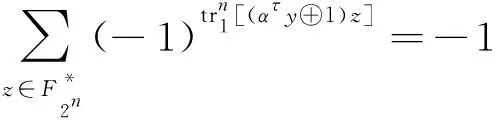
3 结论

参考文献：

[1] Golomb S W.Sequences with randomness properties[R].Baltimore:Glenn L Martin Company,1995.

[2] Golomb S W.Shift register sequences[M].San Francisco, CA:Holden-day,1967;Laguna Hills,CA:Aegean Park,1982.

[3] Scholtz R, Welch L.GMW sequences[J]. Tran Information Theory,1984,30(5):548-553.

[4] Baumert L D.Cyclic difference sets[M]. Berlin:Springer-Verlag,1971.

[5] Lidl R,Niederreiter H.Finite fields[M].Cambridge:Cambridge University Press,1983.

[6] Rosendahl P.Niho type cross-correlation functions and related equations[D].University of Turku,Finland:Genealogy Project,2004.