裁剪优化的Anytime算法
孙 俊,戴国骏,张怀相
(杭州电子科技大学计算机应用技术研究所,浙江杭州310018)
0 引 言
路径规划作为移动机器人和虚拟游戏的关键技术,多年来一直是国内外学者研究的热点。大多已有的经典算法如Dijkstra算法[1],A*算法[2]等都能得出最优路径,然而却并不能保证在一定的时间内完成路径计算。而在现实世界的进行的路径规划经常碰到这样的情况:给予机器人一定量的时间,要求机器人在这个时间限制内得出可能的最好路径。实时算法中的Anytime算法就是一种符合这种有时间约束情况的路径规划算法。目前国内外学者已经研究出一系列的Anytime算法,然而都各有缺点:Zilberstein和Russell的ARUAA算法[3]是一个可行的算法,然而它不能评价每个次优路径相比于最优路径的次优率;MSAUA*算法[4]能够给出这个次优率,然而它对以前信息的重用率很低,以至于要浪费很多计算;ARA*算法[5]也存在着花费过多存储空间和计算时间的问题。本文提出的裁剪优化的Anytime算法旨在解决上述问题。该算法的主题思想是:先在一个宽松的膨胀因子的限制下快速地找到一个可行的次优路径,然后进入循环,通过不断降低膨胀因子来寻找更好的路径,直至时间结束。在每次进入循环之前,都要通过分析非均衡表中的节点情况来裁剪无用节点,只留下下次循环里可能有用的节点,以此来减少程序的存储空间。同时,还可以通过分析裁剪后剩下的节点来判断是否需要跳过下一循环。实验结果表明,该算法相对于ARA*算法取得了时间和空间上的性能提升。
1 算法的直觉来源
ARA*算法是一种启发式的增量搜索算法,是一个比较优秀的Anytime算法。ARA*算法的工作原理是通过多次执行伪A*算法来实现的:首先,ARA*算法的时候设置一个较大的膨胀因子e,然后每次执行(即产生一条路径)后就降低这个膨胀因子e,直到e等于1为止。因此,ARA*算法能够保证在每次搜索出一条路径后,这条路径的长度不大于最优路径的e倍。因此,ARA*算法既能够确定每个循环过程中产生的次优路径的次优率,也很好地重用了以前的计算信息。然而,通过仔细探索此算法的流程,仍能发现它的一些缺点,从而进行改进。
如图1所示,这是ARA*算法在e=2.5时的情况(黑色的栅格代表障碍物,带“*”的栅格代表此时次优路径的节点,灰色的栅格代表循环结束后加入非均衡表的节点,下同)。灰色的栅格,即非均衡表的节点有5个,然而经过分析发现,只有带“+”的2个栅格才有可能是最终所需要的节点。显然,其余的3个栅格完全可以从非均衡表中裁剪掉,从而可以减少存储空间。

图 1 ARA*算法(e=2.5)
如图2所示,这是ARA*算法在e=3,e=2和e=1的3次循环中的情况。虽然在e=3的时候已经得到了最优路径,但是算法却完整地进行了3次循环才结束。通过观察可以发现,在e=3的循环结束时,由于非均衡表中的节点都不可能是最终需要的节点,因此可以判断这个次优路径就是最优路径,从而可以立即结束程序,以此来减少运行时间和计算。
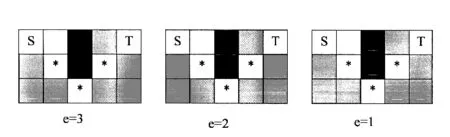
图2 ARA*算法(3次循环)
本文提出的算法就是通过分析每次循环后非均衡表的节点信息,裁剪其中不可能是最终需要的节点来克服以上缺点,提高Anytime算法的性能。
2 算法的过程描述
2.1 算法的定义解释
g(s)表示节点s到起点的路径代价,h(s)表示节点s到终点的估计路径代价,c(s,^s)表示边的代价。OPEN表存放在本次循环中产生的非均衡节点,INCONS表存放在本次循环中已经扩展过的非均衡节点,它的作用是不在一次循环中两次扩展一个节点。由于OPEN表和INCONS表存储的都是非均衡节点,所以把它们统称为非均衡表。e表示膨胀因子,e-fvalue计算的是带膨胀因子的路径代价。
2.2 算法的描述
如下文中的算法伪代码所示,算法共由3个模块组成:Circle Compute、Main、Scissor Modul。
Circle Compute每次从OPEN表中挑出e-fvalue最小的节点,如果它小于终点的e-fvalue值,则扩展它,并产生它的所有后继节点,根据后继节点的产生次数分别放入OPEN表或者INCONS表。
Main是主程序,它先进行初始化,然后在OPEN表中放入起点调用Circle Compute模块完成第一次循环计算,标记本次循环所得路径为当前路径,接着更新e以及合并OPEN表和INCONS表,然后调用Scissor Modul来裁剪OPEN表中节点,根据裁剪结果来判断是否进入下一循环。最终结果是最优路径。
Scissor Modul裁剪OPEN表中的节点,通过分析计算来去除所有不可能是最终需要的节点。然后根据裁剪后的OPEN表来判断是进入还是跳过下一次循环,或者直接跳入Main的结尾。
算法伪代码



3 实验结果与讨论
根据上述算法进行了程序实现,用以评价算法正确性与效率。评价一个算法的效率应该从空间代价和时间代价两个方面着手。对于空间方面,减少表格中的节点总数可以有效的降低程序的空间存储;对于时间方面,由于Anytime算法是通过进入循环模块来产生一系列次优路径的,如果能减少进入循环的次数就能降低时间花费。

表1 SAT算法与ARA*算法的比较
实验通过与Anytime算法中较经典的ARA*算法的比较来说明本算法的效率,并且采用图1的环境模型为例子。实验结果如表1所示:ARA*算法进入了全部的4次循环,而SAT算法通过裁剪分析跳过了2次循环,只进行了2次循环计算;同时,SAT算法在每次循环后保存的节点总数也均比ARA*算法少,这充分显示了裁剪的作用,降低了空间存储。(在是否进入循环的一列中“1”代表进入,“0”代表不进入)
4 结束语
本文根据对已有的Anytime算法优缺点的分析,提出了裁剪优化的Anytime算法。该算法通过裁剪每次循环计算后的非均衡表,有效地降低了程序的存储空间;然后,根据分析裁剪后的非均衡表,来判断是否跳过下一循环,通过跳过若干次循环,降低了时间和计算的花费。实验通过与ARA*算法的比较证明了该算法是有效的。如何利用裁剪后非均衡表中的信息来形成一个更加灵活的膨胀因子变化机制,将是下一步研究的重点。
[1] 张巧荣,崔明义.基于改进Dijkstra算法的机器人路径规划方法[J].微计算机信息,2007,23(1-2):286-287.
[2] Hart P,Nilsson N,Raphael B.A formal basis for the heuristic determination of minimum cost paths[J].IEEE Transactions on Systems Science and Cybernetics,1968,4(2):100-107.
[3] Zilberstein S,Russell S.Approximate reasoning using anytime algorithms[J].In Imprecise and Approximate Computation,1995,1(4):43-62.
[4] Zhou R ,Hansen E.Multiple sequence alignmentusing A*[J].In Proc of the National Conference on Arti?cial Intelligence,2002,13(4):975-976.
[5] Likhachev M,Gordon G,Thrun S.ARA*:Anytime A*with provable bounds on sub-optimality[J].In Advances in Neural Information Processing Systems,2003,16(3):75-83.

