基于EPF滤波的三维单站无源定位算法

许天园，刘顺兰

（杭州电子科技大学通信工程学院，浙江杭州310018）

0 引 言

三维单站无源定位与跟踪技术对于C4ISR系统中的空载电子侦察监视具有重要的价值。利用运动学原理，如果观测器不但观测到目标辐射源相对于观测器的方位角、俯仰角，还可以通过干涉仪、红外或其它手段测量到它们的变化率-方位角变化率或俯仰角变化率，就能够对三维空间中的固定辐射源进行单站无源定位［1］。单站无源定位的本质是一个非线性估计问题，EKF在对非线性模型进行线性化过程中容易引入误差，所以使模型的准确性大大降低，滤波性能次优，甚至导致滤波器发散［2］。本文考虑利用EKF滤波方法作为粒子滤波的重要性函数，即使用EKF对每个粒子点进行局部线性化来完成样本更新，通过融合当前观测数据，以改善参考分布，达到克服粒子退化的目的。通过仿真可以知道基于EPF滤波的单站无源定位比传统的EKF滤波算法好。

1 三维定位模型和方法

假定观测器 0=（x0，y0，z0）T为原点，以速度 V=（v0y，v0y，v0z）T运动，它与固定辐射源 T=（x，y，z）T的距离为，此时固定辐射源的辐射波到达观测器的方位角β及相对俯仰角ε都由于观测器运动而随时间变化，因此观测器可以观测到来波到达方位角变化率，三维定位示意图如图1所示。

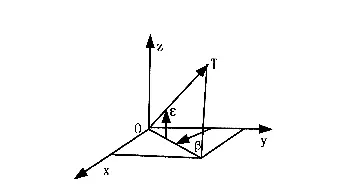
图1 三维定位示意图

由方位角β和俯仰角ε定义可知：

如果辐射源固定时，其在图1坐标系中相对于观测器的运动速度为-v，因此-v0z并令 rh，代入式3可得：

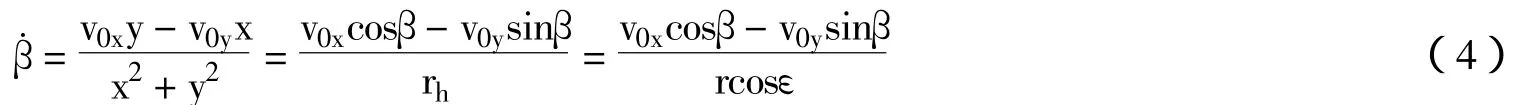
从而可以得到测距公式：

假设获得的观测参数β、˙ β、ε、v0x、v0y含有误差，并假定这些误差之间相互独立且都是零均值的，它们的方差分别为，将式5对这些参数求全微分后得到利用方位角速度定位的三维测距误差方差为［1，2］：

式7可以看出，如果观测器朝目标辐射源径向运动导致˙β=0，或者目标出现在观测器的正下方导致俯仰角ε=90°时，或者观测器在目标斜距矢量所在的等锥上运动时，式7右边变为无穷大，所以利用方位角速度信息定位时在这些情况下是不可观测的。

2 EPF滤波

粒子滤波的核心思想是用随机采样点集以及相应的权值来表示所求的状态变量。粒子滤波具有良好的鲁棒性，受滤波初始误差的影响小，适用于任何非线性高斯情况，这与扩展卡尔曼滤波算法的高斯假设相比是一个很大的优点。粒子滤波的重要性函数选择不好，会导致滤波发散或极差的滤波效果，因而重要性函数对于粒子滤波器的设计是至关重要的［3］。

2.1 数学模型

假定图1中观测器与固定目标存在相对运动，在i时刻的相对距离表示式为：

式中，状态转移矩阵Φ=H。

2.2 EPF 算法描述

（2）用EKF算法更新采样粒子：

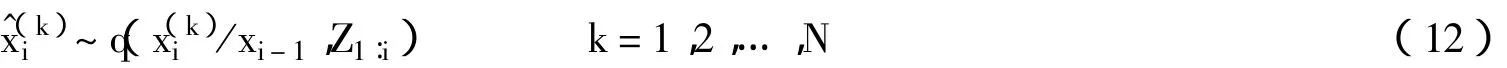
权值更新且归一化权值：

1）累积密度函数（CDF），c1=0；

2）for k=2：H

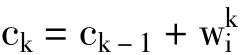
end for；

3）k=1，u-1 ～ U［0，1/N］；

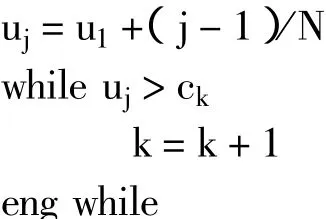
3 仿真结果与分析

假设观测器位于坐标原点以250m/s的速度沿y轴水平匀速运动，固定辐射源位于坐标（100km，50km，5km）处，每隔时间t可以观测到一组测量参数，代入到式5计算出此时的距离rmi，从而得出辐射源的位置，代入EPF滤波算法中，对其进行平滑和修正。参数初值设置如下：测方位角误差σβ为17.4mrad，测俯仰角误差σε为17.4mrad，测方位角变化率误差σ˙β为0.5mrad/s，测俯仰角变化率误差σ˙ε为0.1mrad/s，测速度误差σvx、σvy分别为 0.1m/s，测位置误差σx、σy为 15m，采样时间间隔 t=1s，粒子数 Number=100，仿真结果如图2、3所示。

图2中EKF滤波通过100次蒙特卡罗仿真，EPF滤波则是通过一次观测，由仿真结果可知EPF虽然使用EKF对每个粒子点进行局部线性化来完成样本更新，但它不易对EPF滤波产生影响，该方法不易发散，结果较稳定，而EKF滤波在经过500次迭代后，有发散现象。因此EPF滤波方法要优于EKF方法。衡量定位效果的一个重要标准是定位精度，即相对位置误差，定义为：

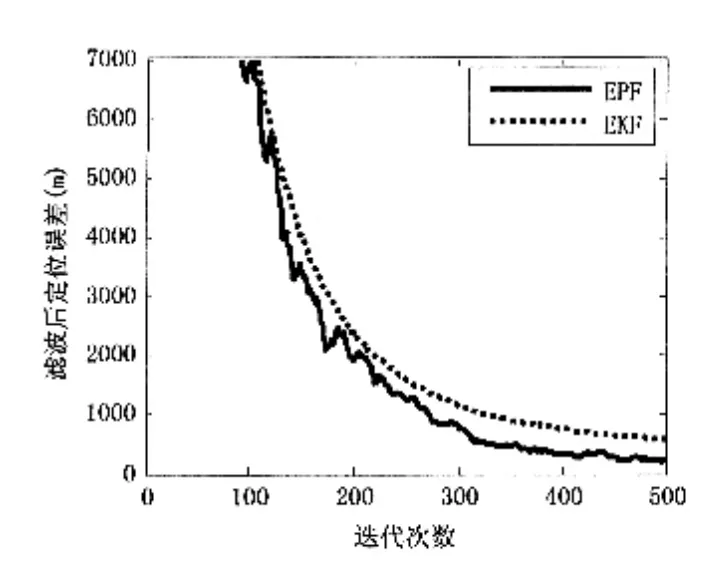
图2 EKF和EPF的定位误差

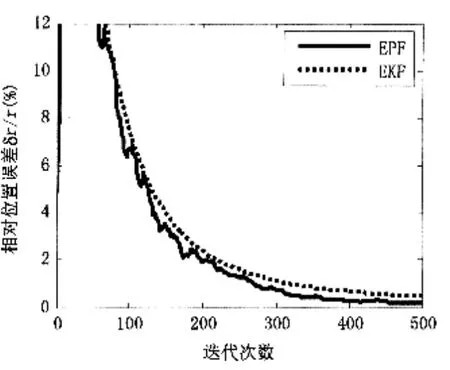
图3 EKF和EPF的定位误差精度

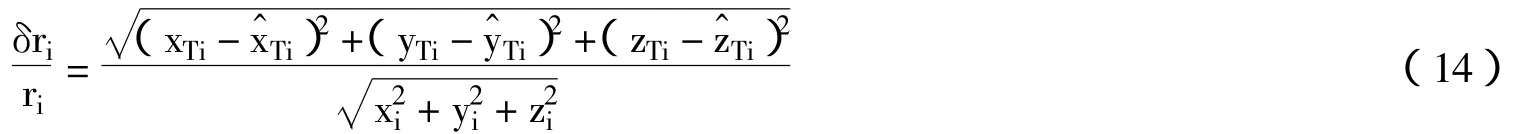
4 结 论

本文将EPF滤波方法应用于三维单站无源定位中，该方法在基本粒子滤波方法中采用EKF对每个粒子点进行局部线性化来完成样本更新，即在更新粒子时包含了最新的观测量信息，提高了粒子滤波算法的性能，有效克服了EKF滤波发散。仿真结果表明EPF滤波方法要优于EKF滤波方法，定位受测量方差初值影响小，具有更好的滤波稳定性，收敛速度更快、更稳定，定位精度更高。

［1］ 郭福成，孙仲康，安玮.利用方向角及其变化率对固定辐射源的三维单站无源定位［J］.电子学报，2002，30（12）：1 885-1 887.

［2］ 郭福成.基于运动学原理的单站无源定位与跟踪关键技术研究［D］.长沙：国防科技大学，2002：1-124.

［3］ 王志刚，陈良友，边少锋.EPF算法在惯导非线性初始对准中的应用［J］.中国惯性技术学报，2007，15（2）：164-167.

［4］ Deng Xiao-long，Xie Jian-ying，Yang Yu-pu.Improved Particel Filter for Passive Target Tracking［J］.Journal of Shanghai University，2005，9（6）：534-538.

［5］ Arulampalam M.Sanjeev，Maskell Simon，Gordon Neil，et al.A Tutorial on Particle Filters for Online Nonlinear/Non Gaussian Bayesian Tracking［J］.IEEE Transactions On Signal Processing，2002，50（2）：174-188.