加权窗口Fourier变换

张志会，胡勇，梁瑜

(湖北大学 数学与计算机科学学院，湖北 武汉 430062)

0 简介

人们在分析信号时，常常需要对信号先作时域局部化处理，例如按要求分段，再作频域分析，也常常需要对信号先作频域局部化处理，例如低频分离处理，频带分离处理和高频分离处理，再用频域信号的改变来获得所需的时域信号.因此人们希望时域和频域都能作出时-频局部化处理.然而，传统的Fourier分析对时-频局部化的要求显然是无能为力的.这就导致了窗口Fourier变换的产生.窗口Fourier变换通过引入一个时间局部化窗口函数来提取信号Fourier变换的局部信息，从而实现了时 -频局部化.随着科学技术的发展，时频分析的方法越来越多，在众多的时频分析方法中，窗口Fourier变换的作用在今天仍然占据很重要的位置.

1 加权窗口Fourier变换

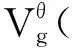
图1 加权窗口Fourier 变换图解

随着时间μ在时间轴上移动，“时间窗”也跟着移动，时域信号f(t)在μ附近被局部化了.现在我们简要地描述一下时窗函数g(t)的时域局部化表现，如图1.从图1可以看出，加权窗口Fourier变换的基本思想就是把信号f(t)划分成许多小的时间间隔，用加权Fourier变换分析每个时间间隔，以便确定该时间间隔存在的频率.

2 加权窗口Fourier变换的定理

可以推出L2(R)空间中函数f(t)的加权Fourier变换与传统的Fourier变换的关系式为

此加权Fourier变换的反演公式为

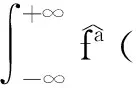
定理1的证明利用上述加权Fourier变换与传统Fourier变换的关系式可得

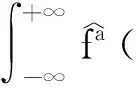
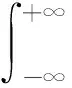
定理2 若f(t)，g(t)∈L2(R)，‖g(t)‖2=1，且为偶函数，则

且有同构公式

定理2的证明可以把加权窗口Fourier变换看作f(t)g(t-μ)的加权Fourier变换，于是下列等式成立

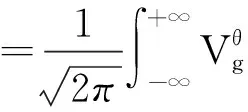
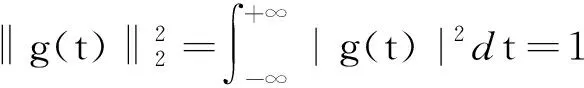
重构公式证完，下面证明同构公式.

两边对μ进行积分

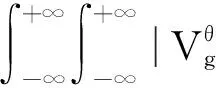
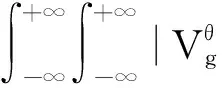
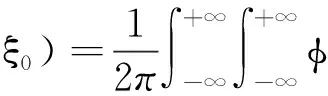
其中K(μ0,μ,ξ0,ξ)=.

定理3的证明必要性.

充分性.定义

利用重构公式

参考文献：

[1] Qian Tao.Unit analytic signals and harmonic measures[J].Mathematical Analysis And Applications,2006,314:526-536.

[2] Qian Tao,Chen Qiuhui,Li Luoqing.Unit analytic quadrature signals with nonlinear phase[J].Physica D:Nonlinear Phenomena,2005,203(1-2):80-87.

[3] Chen Qiuhui,LI Luoqing,Qing Tao.Time-frequency aspects of nonlinear Fourier atoms[J].Applied and Numerical Harysis,2004,287-297.