主理想整环上的模的性质

王俊燕

(湖北大学 数学与计算机科学学院，湖北 武汉 430062)

1 预备知识

为了讨论的方便，以下总设R为一个主理想整环，M为一R-模，p为R中的素元，S=R(〗0}，S-1R为R的商域.

定义1 若对任意的m∈M和任意的非零因子a∈R，总有m′∈M，使得m=am′，则称m为可除元.若M中的任意元均为可除元，则称M为可除模.

设M为R-模，N为M的子模，若方程rx=z,r∈R,z∈N在M中有解，则在N中也有解，则称N为M的纯子模.显然,若对任意的r∈R，都有rM∩N=rN，则N为M的纯子模.

设B为M的子模，若B为纯子模且为循环模的直和，M/B为可除模，则称B为M的基子模.

设m∈M，若m=phm′,m′∈M且m∉ph+1M，则称h为m的p高.

引理1 若M为一扭模，则M为它的p-分量的直和.

引理2 若D为M的可除子模，则M=D⊕E，其中E为M的子模.

引理2的证明设l：D→M为一包含映射.由可除模的内射性可得存在一模同态β：M→D，使得lβ=1即dβ=d，对∀d∈D.若m∈M，则mβ∈D，mβ=mβ2，故m-mβ∈kerβ=E，故M=D+E.若d∈D∩E，则d=dβ=0.故M=D⊕E.

引理3 若M可以用不同的方式表示为拟循环模、循环p-模、无限循环模的直和，则在不同的分解中同构的类型的直和项具有相同的势.

引理3的证明首先在任何一种分解中无扭的直和项具有相同的势，而对扭模，由引理1可不妨设M为一p-模，在任何一种分解中直和项为M(pn+1)的势等于pnM∩M(p)/pn+1M∩M(p)仅与M有关，而对拟循环p-模的直和项生成M的极大可除子群D的p-分量，形成一势为dim(D(p))的集合，因此结论成立.

2 主要定理

定理1 模M为可除模当且仅当M同构于若干个S-1R与拟循环模的直和.

定理1的证明(充分性)S-1R和拟循环模均为可除模，而可除模的直和仍为可除的，因此M为可除模.

(必要性)设T为M的扭子模，断言T为可除的.事实上由M为可除模可得对x∈T，任意的r∈R，存在y∈M，使得x=ry.但是M/T为无扭的，故y∈T.因此T为可除的.由引理1可得T为它的p-分量的直和，每个p-分量都是可除的，由引理2可得T为M的直和项，因此只需证明两种情形M为无扭的与M为一p-模.

φ：M×S-1R→M，

则M为一S-1R-模，而S-1R为一域，从而M为S-1R上的向量空间，故M同构于若干个S-1R的直和.

设M为一p-模，p=M(p)，其中p为一素元.理想(p)为一极大理想，故R/(p)为一域.定义

φ∶P×R/(p)→P,

(x,r+(p))→rx,

则p为一R/(p)-模，从而P为R(p)上的向量空间，设维数为c.令M*为c个拟循环p-模的直和，P*=M*(p)，则P*为R/(p)上的c维向量空间.故存在一单同态α：P*→M使得P*同构于P，由可除模M的内射性质可得存在β：M*→M，使得βP*=α.若kerβ≠0，则α不为一单同态.若Imβ≠M，则可除模Imβ为M的直和项，这就与单同态α使得P*同构于P相矛盾.因此β为一同构映射.

综上可得M同构于若干个S-1R与拟循环模的直和.

定理2 可除模M的纯子模H为M的直和项.

定理2的证明首先可除R-模M为一S-1R模，H为M的纯子模，故H也为S-1R模.令集合J={Aα：Aα为S-1R-模的子模且Aα∩H=0}，由佐恩引理可得J中存在极大元A，即A为S-1R-模且A∩H=0.以下证明M=H+A.

定理3 M为p-模，M为可除的当且仅当M没有非平凡的纯循环子模.

定理3的证明(必要性)M为p-可除模，由定理1可得M≃CrGn，Gn为p-拟循环模，设H为M的纯子模，由定理2可得H为M的直和项，但H不可能为循环子模.故M没有非平凡的纯循环子模.

(充分性)若M(p)中的任意一元均有无限p高，假设M不为可除模，则存在不被p整除的元m，不妨取最小的正整数t使得ptm=0而ptm=ppt-1m=0则pt-1m∈M(p)有无限p高，故pt-1m=ptm1，m1∈M，pt-1(m-pm1)=0，令m2=m-pm1,则pt-1m2=0.重复上述过程可得m2=pm3因此m=m2+pm1=p(m3+m1),这就与m不被p整除矛盾.因此M为可除模.故若M不为可除模，M(p)中必存在一元素具有有限p高.

在进行位置分析时，用a、b、c、d来表示4个构件的长度，根据矢量方向和方位的选择(由箭头指明)如图3所示，得到了下面的矢量环方程：

综上可得M不为可除模，则M有非平凡的纯循环子模.

定理4 M满足极小条件当且仅当M为有限多个拟循环模与有限循环p-模的直和.

定理4的证明(必要性)M满足极小条件，若M为一无扭模，即对任意的m∈M，不存在r∈R，使得rm=0，则Rm>R2m>R4m>…为一无限链，无极小元，与M满足极小条件相矛盾.因此M为一扭模，由引理1可得M为它的p-分量的直和，可设M为一p-模.

若M中有可除元，由引理2可得M=E⊕H，其中E为可除模，H中无可除元.由定理1可设M为一既约模，无可除元，只需证明M为有限循环模.假设M为无限模，由M满足极小条件可得存在M的极小无限子模H，若H=pH，则H为可除模，而M为既约模，故H=0.因此H>pH，由H的极小性可得pH为有限的，由模的同构定理可得H/H(p)≃pH.故H/H(p)为有限模，H(p)为一无限模，H的极小性使得H(p)为有限模，矛盾.因此M为有限模，也必为有限生成的，可以分解为有限多个循环p模的直和.

(充分性)拟循环模的每个真子模均为有限的，因此拟循环模满足极小条件.不妨设M=D⊕E，D为有限个拟循环模的直和，E为有限循环p-模的直和，则M/D≃E，满足极小条件.因此M满足极小条件.

定理5 M为一扭模，则M有基子模且M的所有基子模均同构.

定理5的证明若Dp为M的p-分量的基子模，则D=DrpDp为M的基子模，因此不妨设M为一p-模.若M为可除模，则0为M的基子模，可设M不为可除模.

若非空集合X中的元线性无关且由X生成的模为纯子模，则称X为纯无关集.由定理3可得纯无关集存在.按包含关系可得一纯无关子集链，这条链上的元的并为纯无关的.由佐恩引理可得存在一极大纯无关子集X，令B为由X生成的纯子模.

若M/B不为可除模，则由定理3可得M/B有非平凡的纯循环子模R(m+B).若pdm∈B,则pdm∈pdM∩B=pdB.因此pdm=pdb,b∈B，故pd(m-b)=0.由(m-b)+B=m+B，可设m′=m-b,则pdm′=0.同时pd(m′+B)=0M/B.令Y=X∪{m′}，若Y为线性相关的，则存在r∈R，使得0≠rm′∈B，即r(m′+B)=0M/B,由上面的讨论可得rm′=0，矛盾.因此Y线性无关.B为M的纯子模，R(m′+B)/B为M/B的纯循环子模，令K=R(m′+B),设k∈aM∩K，a∈R，则k=am，m∈M，而k+B=am+B=a(m+B)，由K/B为M/B的纯子模可得k+B=a(k′+B)，k′∈K,则h=k-ak′=am-ak′=a(m-k′).由B为M的纯子模可得h=ah′,h∈B.因此k=ah′+ak′=a(h′+k′)∈aK，故K为M的纯子模.因此由Y生成的子模为M的纯子模且Y线性无关，因此Y为纯无关子集，这就与X的极大性相矛盾.因此M/B为一可除模.故B为M的基子模.

由M/B为一可除模可得对任意的n≥0，M=pnM+B，同时由B为M的纯子模可得pnM∩B=pnB且M/pnM≃B/pnB.若k≤n，则B的直和项中M(pk)的循环模的个数=B/pnB中对应的个数=M/pnM直和分解的循环模的个数.由引理3可得任意两个基子模同构.

3 基子模的一个实例

事实上，对任意w∈B，

若w=pg，g∈M，则w=pg=p∑bixi=∑(ai-ai-1pni-ni-1)xi,

因此

∑(pbi-ai+ai-1pni-ni-1)xi=0,

故

pnipbi-ai+ai-1pni-ni-1.

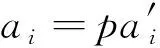
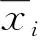
对任意的i，

xi+B=pni+1-nixi+1+B=p(pni+1-ni-1-1xi+1+B)=P(yi+B).

任意的g+B∈M/B，

而∑ciyi+B∈M/B.继续此过程可得对任意的t，存在h∈M，g+B=pt(h+B),即M/B为一可除模.

因此B为M的基子模.

参考文献：

[1] DereK J S Robinson.A course in the theory of groups[M].New York:Spring-Verlag,2001.

[2] Frank W,Anderson K,Fuller R.Rings and categories of modules[M].New York:Springer-Verlag,1992.

[3] 聂灵沼，丁石孙.代数学引论[M].北京：高等教育出版社，2000.

[4] 陈家鼐．环与模[M].北京：北京师范学院出版社，1989.