基于小波理论光子晶体能带计算中小波积分的解析求解

刘冬梅， 韩 鹏， 郑楚君

(华南师范大学物理与电信工程学院，广东广州 510631)

基于小波理论光子晶体能带计算中小波积分的解析求解

刘冬梅， 韩 鹏*， 郑楚君

(华南师范大学物理与电信工程学院，广东广州 510631)

详细推导了基于双尺度关系的小波积分的矩阵本征值求解方法．并选择常用的Harr小波和CDF小波进行了实际计算，与数值积分的方法进行了比较，结果表明该方法具有良好的精度．同时，还针对光子晶体的特点，对该方法进行了改进，这将有利于进一步提高基于小波理论的光子晶体计算方法的性能．

小波积分； 光子晶体； 本征值求解

自从1987年YABLONOVITCH、GMITTER[1]和JOHN[2]分别提出光子晶体和光子能带结构的概念以来，光子晶体的理论研究和相关实验及其应用得到了迅速的发展.由于光子能带具有一系列崭新的特性，如频率落在完全光子带隙内的电磁波(光波)不能在光子晶体内的任何方向传播和抑制自发辐射等[3].光子晶体的这些奇特性质激起了人们对它的理论和实验研究的广泛兴趣，促使人们去研究光子晶体的各种可能的效应和应用，因此，近年来光子晶体的研究成为人们普遍关注的研究热点.

光子晶体的大部分性质是通过它的能带计算得到的，因此，晶体能带的有效计算是研究光子晶体的关键.这样就要求找到一个效率和精度都很高的算法来计算光子晶体的能带结构.常用的能带计算方法有传递矩阵法(TM)、平面波展开法(PWE)、多散射理论法(MST)和有限差分时域法(FDTD)等.变分法(VM)是计算光子晶体能带的重要方法，它是把场和介电函数向一系列的基函数上展开，平面波展开法就属于这一类，平面波法是向平面波上展开，但收敛慢一直是平面波法的主要缺点之一.

小波理论[4]用于光子晶体能带结构的计算具有精度高、收敛快等优点[5-6].小波法选的是小波基，在该方法中，小波积分的解析求解是整个算法的关键，也是该方法高精度的保证[7-8].因此用解析的方法来精确求解小波积分对整个算法的精度非常重要.在数学上已经有人提出了基于双尺度关系的小波积分求解方法，但那是通用型的，且过程很复杂.我们针对光子晶体这个特殊对象把计算过程进行了优化.本文详细推导了基于双尺度关系的小波积分的矩阵本征值求解方法，给出了算法的流程.并选择常用的Harr小波和CDF小波进行了实际计算，与数值积分的方法进行了比较，结果表明小波法具有良好的精度.

1 小波方法计算光子晶体

×{).

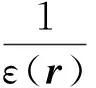
(1)

选择TE模的情况来讨论，要求解上述方程可以对方程两边与测试函数作内积，在每一个原胞Ω上，所有的平方可积函数u具有平方可积的一阶导数，上面的第2个等式可以表示成下面的形式：

(2)

利用变分法，对所有的u，式(2)可以等效为积分的形式

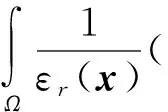
(3)

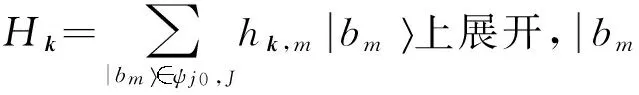
式(3)可以写成矩阵的形式Akνk=Bνk，Ak和B是大稀疏矩阵，νk是包含hk,m的列向量.其中

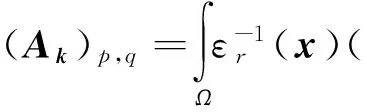
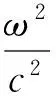
(4)

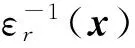
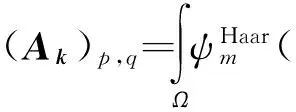
(5)

求解式(5)的关键是要求积分

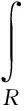
(6)

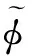
2 小波积分的矩阵法求解

主要是解决3个尺度函数相乘的积分问题，它的形式如下：

(7)

其中上、下标0、1、2仅仅是标识，ψ0、ψ1、ψ2都是尺度函数，α0、α1、α2是平移量，其中α0可以取0，…，2k0-1；α1可以取0，…，2k1-1；α2可以取0，…，2k2-1.k0、k1、k2是伸缩量，为常数.

计算的主要思路是：

①

②

③

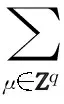
①表示把x前面的系数全部变为1；②表示把函数ψ0中的平移量变为0；③表示构建本征方程．具体做法如下所述.

2.1变x前面的系数为1

式(7)中的ψ0、ψ1、ψ2都满足双尺度关系，即：

(8)

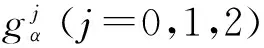
I(α0,α1,α2;k0,k1,k2)=

(9)

可以把式(9)简化为求解I(0,α1,α2;0,0,0)的值，用H(x1,x2)来表示积分I(0,α1,α2;0,0,0).下面来证明积分式(9)可以由积分H精确确定，即

(10)

I(α0,α1,α2;k0,k1,k2)=

2qrI(α0,α1,α2;k0+r,k1+r,k2+r).

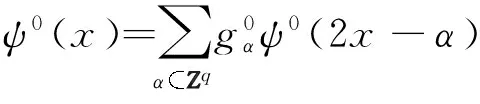
I(α0,α1,α2;0,k1,k2)=

ψ1(2k1-1x-α1)ψ2(2k2-1x-α2)dx,

也就是

I(α0,α1,α2;0,k1,k2)=

(11)

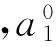
对ψ0重复使用(k1-1)次双尺度关系和变量替换，直到k1=0，也就是让ψ1中x前面的系数变为1.有

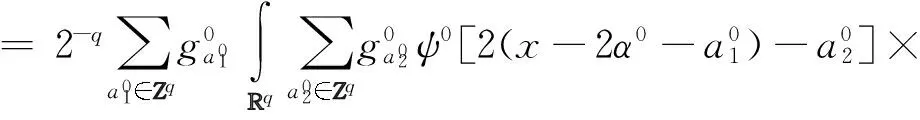
ψ1(2k1-1x-α1)ψ2(2k2-1x-α2)dx=

ψ1(x-α1)ψ2(2k2-k1x-α2)dx=

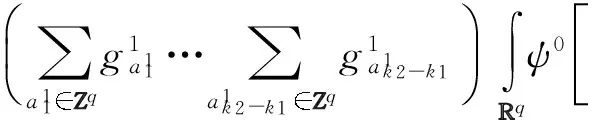
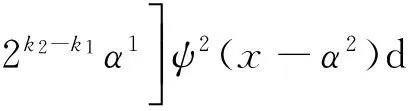
在上式的计算中，对ψ0和ψ1同时使用双尺度关系和变量替换.经过这些计算，因为各个函数对应的滤波器系数是知道的.所以只需要计算积分

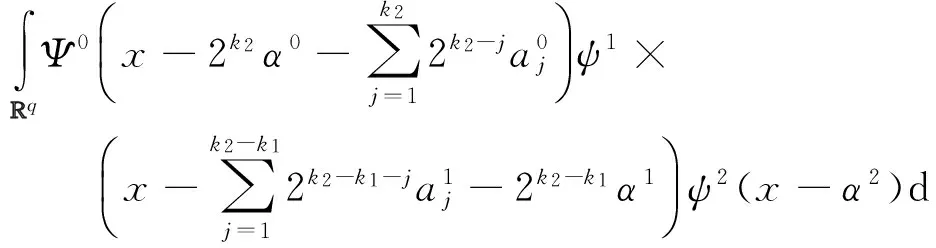
上述的积分式中，x的系数都降为1．这样，我们就完成了第一步.

2.2函数ψ0中的平移量变为0

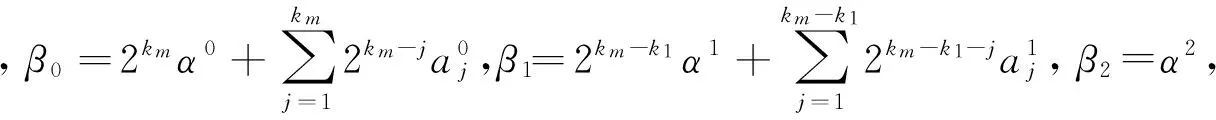
为讨论方便，我们用H(x1,x2)表示上面的积分.

2.3构建本征方程

把式(8)的双尺度关系代入积分式(10)得

2x1-γ1)ψ2(2x-2x2-γ2)dx,

(12)

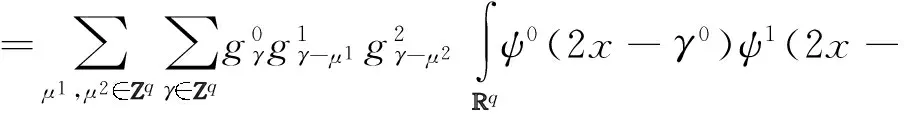
2x1-γ+μ1)ψ2(2x-2x2-γ+μ2)dx=

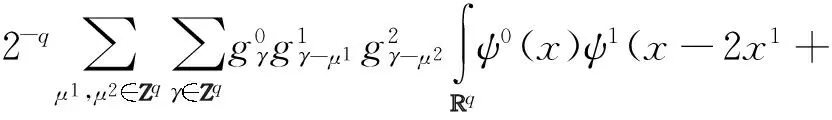
ψ2(x-2x2+μ2)dx=

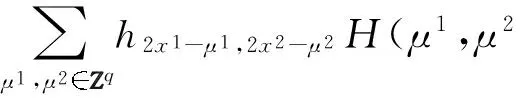
(13)

在倒数第2个等式中采用了变量替换，用(2xj-μj)代替μj，且

(14)

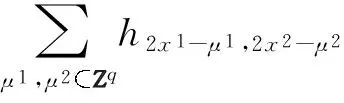
2.4讨论

(1)在光子晶体的能带计算中，由于介电函数ε(x)在晶体的交界处是阶跃性的，不连续的.要把它在基函数上进行展开，就要找一个和它相似的基函数.而在小波基函数当中，Haar小波函数是最佳的选择，它能准确地把介电函数在交界处的变化表示出来，所以在积分当中通常会使用Haar函数.另外，Haar函数还有一个特殊的性质，就是只有在平移量为0和1时，它的滤波器系数才存在，其他情况下全为0.这样3个函数相乘的积分形式就可以进一步简化，式(14)可以表示成

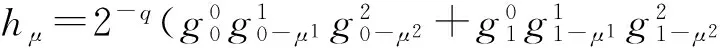
(15)

(2)前面讨论的是3个尺度函数相乘的情况，如果是3个小波函数，就要用小波函数和尺度函数之间所满足的双尺度关系，首先将小波函数转化为尺度函数，然后再按照上面的步骤进行运算.

(3)本文详细讨论的小波积分是针对一维光子晶体能带计算的，如果需要计算二维、三维光子晶体，需要将上面讨论的一维小波变成二维、三维小波，这时小波函数相乘时需要对其进行相应的展开，但上述解析求解方法的思路是一致的．

3 矩阵法与数值法的结果比较

为了验证算法的有效性，我们将矩阵法与传统的数值法进行了比较，其中数值法我们直接采用梯形算法.首先验证了2个小波相乘的积分，选择的是ψHaar函数(图1)和ψCDF函数(图2(a))，计算结果完全一致，都只有在平移量为0和1时有非零值，为0.5.

然后，计算了3个函数相乘的积分情况，在这里ψ0、ψ1和ψ2分别选择了Haar小波和具有双正交关系的Cohen-Daubechies Feauveau(CDF24)小波(图2)来进行计算，在数值计算中，采用了梯形积分的方法.取的是本征值为1时的本征矢，计算的结果如表1所示.

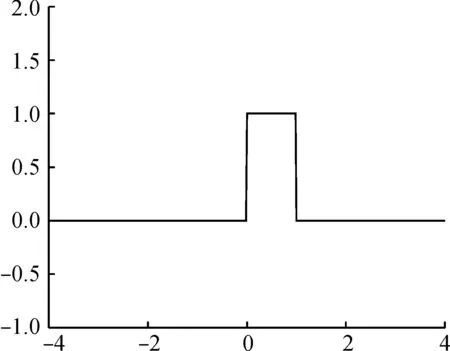
图1 Haar尺度函数ψHaarFig.1 Haar scaling function ψHaar

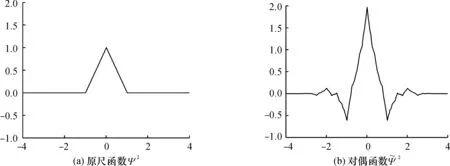
图2 Cohen-Daubechies Feauveau(CDF24)小波Fig.2 Cohen-Daubechies Feauveau (CDF24) wavelet表1 CDF24矩阵法与数值法的结果比较Tab.1 CDF24 comparision between numerical and matrix methods

H(α1,α2)数值计算解小波解析解ΔH(0,-4)0 0 0 H(0,-3)0.000370.000350.00002H(0,-2)0.016350.015730.00062H(0,-1)-0.12126-0.11832-0.00294H(0,0)0.514480.514470.00001H(0,1)0.120000.118220.00178H(0,2)-0.01647-0.01576-0.00071H(0,3)-0.00030-0.000350.00005H(0,4)-0-00

为了检验算法的准确性，我们用这2种方法又计算了Cohen-Daubechies Feauveau(CDF37)(图3)的小波积分，计算结果如表2所示．

从表1和表2中的结果可以看出2种方法计算的积分值非常接近.由于数值方法采用的是梯形积分法，涉及到把图形离散化来取点，存在一定的误差，而小波法就只需知道平移量所对应的滤波器系数，再相乘来求解本征值为1时的本征矢即可，因此，小波积分的优越性和高精度性就体现出来.

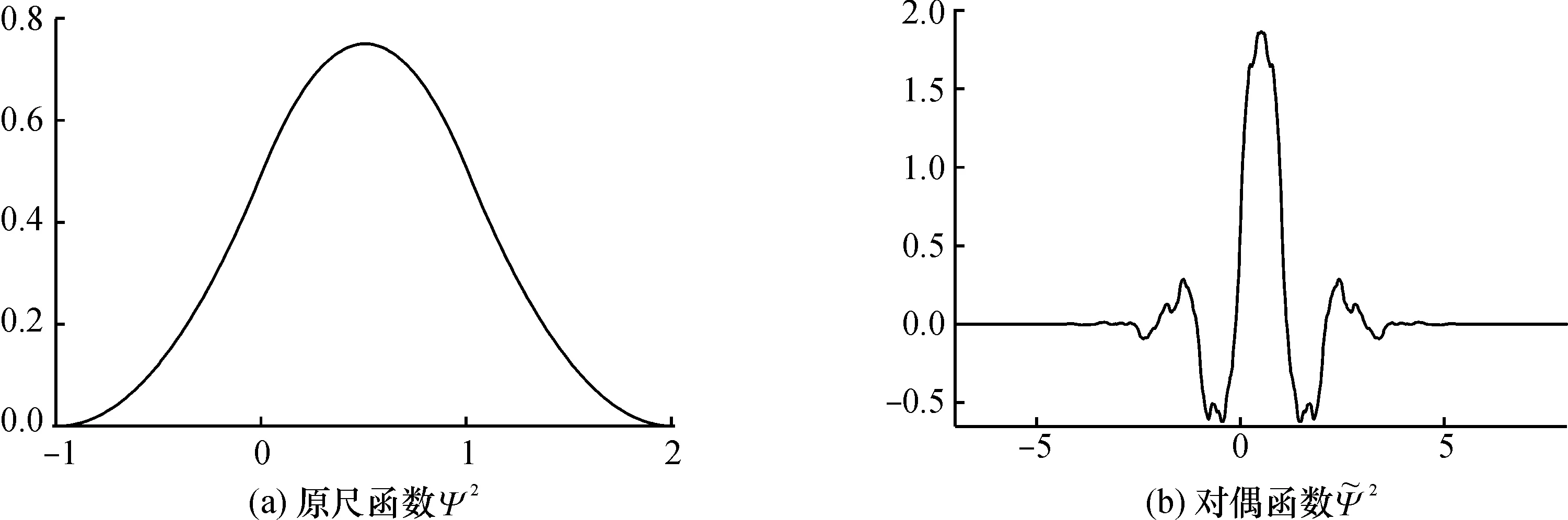
图3 Cohen-Daubechies Feauveau (CDF37)小波Fig.3 Cohen-Daubechies Feauveau (CDF37) wavelet表2 CDF37矩阵法与数值法的结果比较

Tab.2 CDF37 comparision between numerical and matrix methods

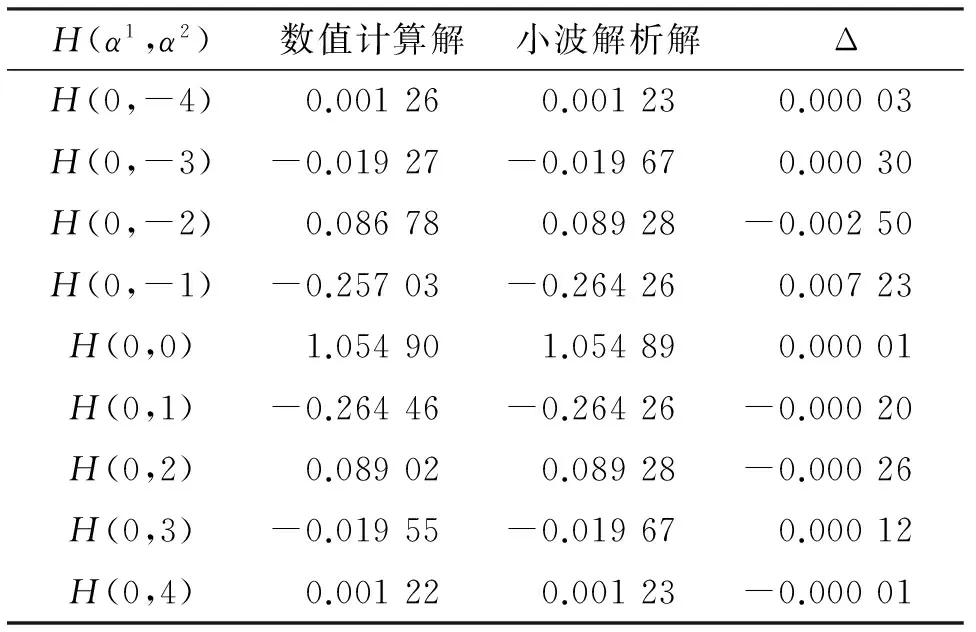
H(α1,α2)数值计算解小波解析解ΔH(0,-4)0.001260.001230.00003H(0,-3)-0.01927-0.019670.00030H(0,-2)0.086780.08928-0.00250H(0,-1)-0.25703-0.264260.00723H(0,0)1.054901.054890.00001H(0,1)-0.26446-0.26426-0.00020H(0,2)0.089020.08928-0.00026H(0,3)-0.01955-0.019670.00012H(0,4)0.001220.00123-0.00001

4 总结

本文详细讨论了基于小波法光子晶体能带结构计算中小波积分的矩阵本征值法精确求解方法.该方法主要利用了小波函数的双尺度关系，通过一系列的变量替换，构造出了本征方程.指出求解该本征方程对应本征值为1时的本征矢量即是所要求解的小波积分.与传统的数值法进行了比较，结果证明了矩阵本征值的正确性.同时由于该方法没有引入任何近似，所以可以预见具有更高的精度.

由于变分法求解微分方程具有一定的普适性，而微分方程在物理学中应用非常普遍，因此本文讨论的小波积分方法将不仅适用于光子晶体的性质计算，在所有基于小波基函数的计算方法中都有可能涉及，具有广泛的应用前景.

[1] YABLONOVITCH E，GMITTER T J. Inhibited spontaneous emission in solid-state physics and electronics[J]. Phys Rev Lett, 1987, 58, 2059.

[2] JOHN S. Strong localization of photons in certain disordered dielectric superlattices[J]. Phys Rev Lett, 1987,58, 2486.

[3] SAKODA K. Optical properties of photonic crystals[M]. Berlin:Spring-Verlag, 2001.

[4] MALLAT S. A wavelet tour of signal processing (信号处理中的小波导引)[M]. 杨力华,戴道清，黄文良，等译. 北京:机械工业出版社,2002.

[5] CHECOURY X, LOURTIOZ J M. Wavelet method for computing band diagrams of 2D photonic crystals[J]. Opt Commun, 2006, 259: 360-365.

[6] YAN Z Z, WANG Y Sh. Wavelet-based method for calculating elastic band gaps of two-dimensional photonic crystals[J]. Phys Rev B,2006, 74: 224303.

[7] DAHMEN W.Wavelet and multiscale methods for operator equations[J].Acta Numerica, 1997,6: 55.

[8] BERTOLUZZA S, CANUTO C,URBAN K. On the adaptive computation of integrals of wavelets[J]. Appl Numer Math, 2000,34:13-38.

Keywords： wavelet integration； photonic crystals； eigenvalue problem

【责任编辑 庄晓琼】

收稿日期： 2009-10-15

基金项目： 国家自然科学基金资助项目(60877069)；广东省科技攻关资助项目(2007A010500011，2008B010200041)

作者简介： 曾坤(1983—)，男，华南师范大学2007级硕士研究生,Email:xus006@163.com；郭志友(1959—)，男，华南师范大学教授级高工，主要研究方向：发光材料与器件，Email:guozy@scnu.edu.cn.

*通讯联系人

ANALYTICALRESOLUTIONOFWAVELETINTEGRATIONINBANDCALCULATIONFORPHOTONICCRYSTALSBASEDONWAVELETMETHOD

LIU Dongmei, HAN Peng, ZHENG Chujun

(School of Physics and Telecommunication Engineering,South China Normal University, Guangzhou 510631, China)

A detail derivation of an analytical method to calculate the wavelet integration based on the eigenvalue problem is presented. The wavelet method and the numerical method are adopted to compute the integral of wavelet with the Haar wavelet and the Cohen-Daubechies Feauveau (CDF) wavelet. The comparative results show the high precision of the wavelet method. Furthermore, the wavelet method is also improved according to the features of photonic crystals, which will facilitate the performance of the algorithm based on wavelet method.

2009-10-10

国家自然科学基金资助项目(10504008)；教育部科学技术研究重点项目(209091)

刘冬梅(1981—)，女，湖南邵阳人，华南师范大学2007级硕士研究生，Email:liudongmei8720@126.com；韩鹏(1976—)，男，安徽潜山人，华南师范大学教授，主要研究方向：光学，Email:hanp@scnu.edu.cn.

*通讯作者

1000-5463(2010)03-0053-05

O29

A