某类解析函数子类的性质与特征

刘志文, 刘名生

(华南师范大学数学科学学院, 广东广州 510631)

某类解析函数子类的性质与特征

刘志文, 刘名生*

(华南师范大学数学科学学院, 广东广州 510631)

引入和研究了解析函数子类Mn(α,β)的一些有趣性质.特别地,得到了这类函数的几个包含关系、充分条件和 Fekete-Szegö不等式等性质.

解析函数; 包含关系; 系数估计; Fekete-Szegö不等式

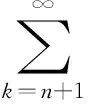
的全体解析函数所成的函数类.

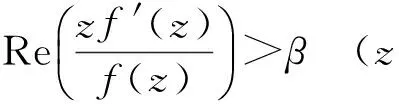
的全体解析函数所成的函数类.

(1)

LI和OWA在文献[1]中证明了：

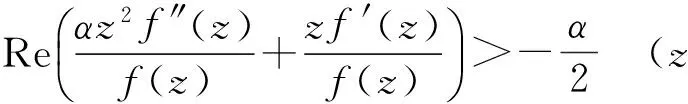
RAVICHANDRAN等[2]对定理1进行了如下改进:

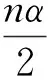
(2)

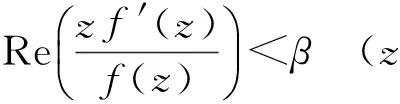
的全体解析函数所成的函数类Mn(β)的一些性质.本文在此基础上研究如下定义的函数类Mn(α,β)的有趣性质,得到了包含关系、充分条件和 Fekete-Szegö不等式等.

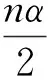
(3)

1 若干引理

为了证明本文的主要结果, 我们需要如下引理.

引理1[9]令Ω表示复平面中的一个集合, 假设Φ是2×U到的一个映射. 并且对所有满足y≤-n(1+x2)/2的实数x,y和所有的zU,都有Φ(ix,y;z)Ω.若函数p(z)=1+cnzn+… 在U上解析且对所有的zU,都有Φ(p(z),zp′(z);z)Ω, 则Re(p(z))>0,zU.

并且上述结果是精确的.

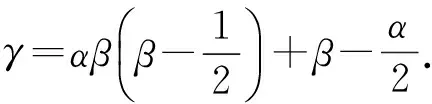
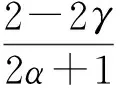
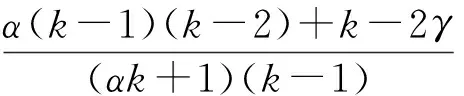
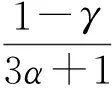
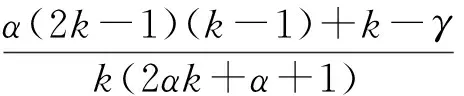
证明由于

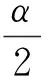
通过简单计算及对比两边系数,可知f0(z)和f1(z)满足如下关系式:

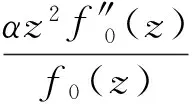
和

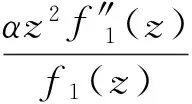
因此

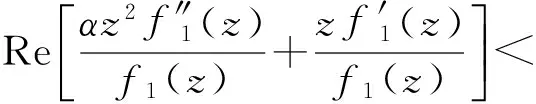
2 主要结果

首先, 我们证明了函数类Mn(α,β)的如下几个包含关系.

证明令

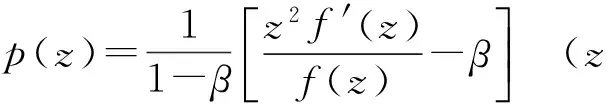
则p(z)=1+cnzn+… 在U内解析. 通过简单计算可得

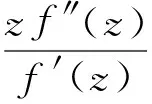
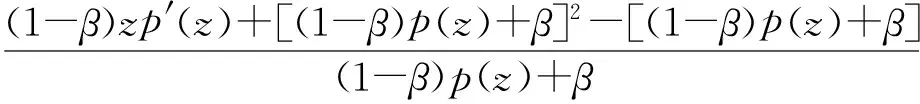
因此

α(1-β)zp′(z)+α(1-β)2p2(z)+

(1-β)(1+2αβ-α)p(z)+β(αβ+1-α)=

Φ(p(z),zp′(z);z),

其中

Φ(r,s;t)=α(1-β)s+α(1-β)2r2+

(1-β)(1+2αβ-α)r+β(αβ+1-α).

因为α≥0且1<β≤1+n/2,则对所有满足y≤-n(1+x2)/2 的实数x,y, 我们有

ReΦ(ix,y;z)=

α(1-β)y-α(1-β)2x2+β(αβ+1-α)≥

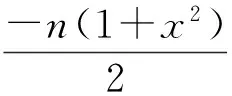
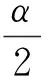
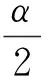
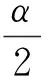
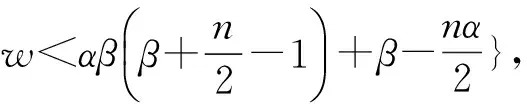
在定理3中令β=α/2,n=1, 可得如下推论.

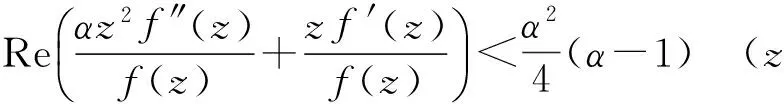
通过应用定理3, 我们得到：

定理4 设α1>α2≥0,1<β1<β2≤1+n/2, 那么

Mn(α1,β1)⊂Mn(α2,β2).

(4)

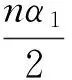
(5)

由于α1>α2≥0,1<β1<β2, 则有

(6)

因此由式(5)和式(6),可以得到

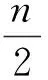
(7)

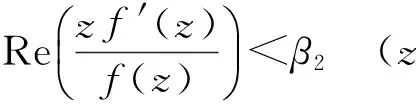
(8)

令α=α2/α1, 则0≤α<1,于是由式(7)和式(8), 可得

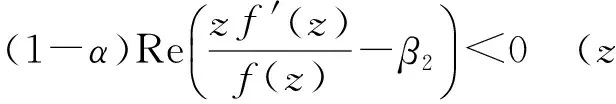
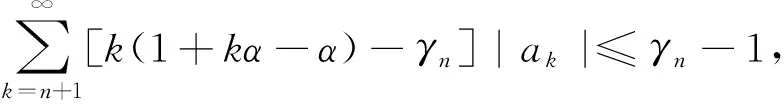
(9)

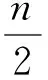
证明由于α≥0,β>1, 我们有

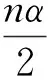
对于函数

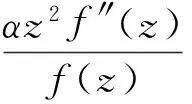
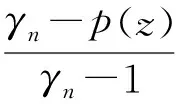
由系数不等式(9), 我们可以得到

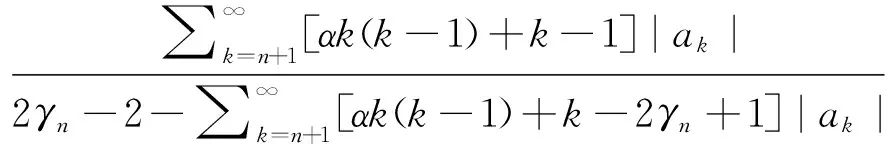
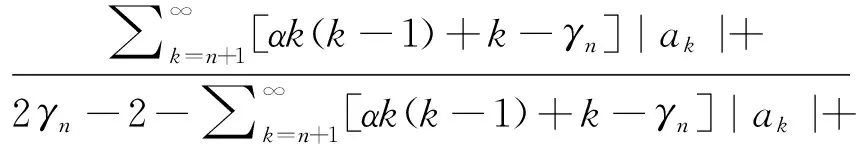
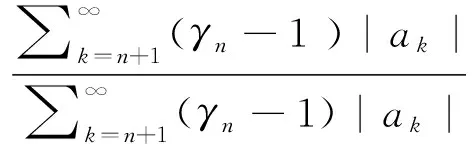
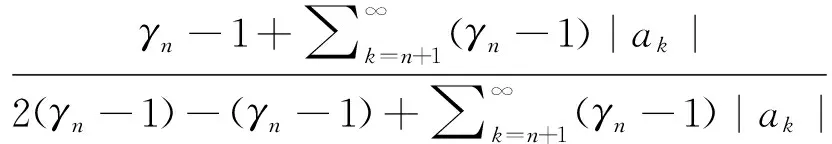
最后,我们研究函数类M1(α,β)的Fekete-Szegö不等式性质.

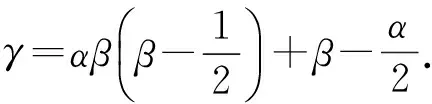
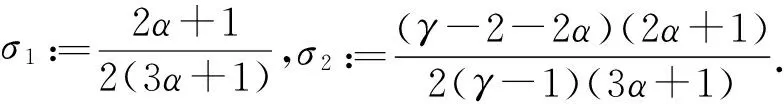
这些结果都是精确的.

p(z)f(z)=γf(z)-(αz2f″(z)+zf′(z)).

(10)

因为

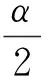
我们有

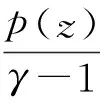
(11)

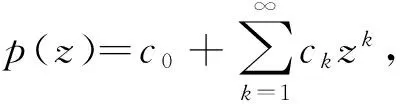
对比上式两边系数可得

由于c0=γ-1,则有

也即

(12)

由式(11), 若令h(z)=1+h1z+h2z2+…, 则可得

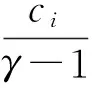
则由式(12),我们有

从而可得

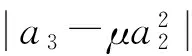
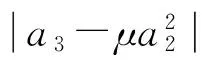
因此,应用引理2可知定理6的结论成立.

最后,为了证明定理6中不等式的精确性,我们分以下2种情况讨论：

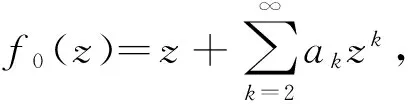
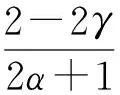
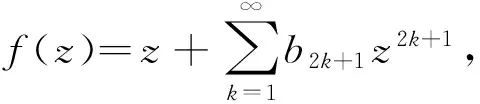
[1] LI J L,OWA S. Sufficient conditions for starlikness[J]. Indian J Pure Appl Math,2002,33:313-318.

[2] RAVICHANDRAN V,SELVARAJ C,RAJALAKSMI R. Sufficient conditions for starlike functions of order α[J]. J Inequal Pure Appl Math,2002, 3(5): Article 81, 6pp.

[3] LIU Mingsheng,ZHU Yucan,SRIVASTAVA H M. Pro-perties and characteristics of certain subclasses of starlike functions of orderβ[J]. Mathematical and Computer Modelling,2008,48:402-419.

[4] 李宗涛, 刘名生. 一类解析函数的系数泛函[J].华南师范大学学报:自然科学版, 2005(3): 86-91.

LI Zongtao, LIU Mingsheng.The functional of coefficients for a class of analytic functions[J].Journal of South China Normal University:Natural Science Edition,2005(3): 86-91.

[5] 郭栋, 刘名生. 关于解析函数类的Fekete-Szegö问题[J].华南师范大学学报:自然科学版, 2007(2): 33-38.

GUO Dong, LIU Mingsheng.On the Fekete-Szegö problem for the class of analytic functions[J].Journal of South China Normal University:Natural Science Edition,2007(2): 33-38.

[6] 刘名生, 石莉芬. 星像函数和关于k折对称点近于凸函数的一些充分条件[J].华南师范大学学报:自然科学版, 2007(3): 1-7.

LIU Mingsheng, SHI Lifen.Some sufficient conditions for starlike and close-to-convex functions with respect tok-symmetric points[J].Journal of South China Normal University:Natural Science Edition, 2007(3): 1-7.

[7] 宋年胜, 刘名生.两类解析函数子类的包含关系和卷积性质[J].华南师范大学学报:自然科学版, 2008(4):32-37.

SONG Niansheng, LIU Mingsheng.Inclusion relation and convolution properties for two subclasses of analytic functions[J].Journal of South China Normal University:Natural Science Edition,2008(4):32-37.

[8] OWA S,NISHIWAKI J. Coefficient estimates for cettain classes of analytic functions[J]. J Inequal Pure Appl Math, 2002,3(5): Article 72, 5pp.

[9] MILLER S S, MOCANU P T. Diffierential subordinations and inequalities in the complex plane[J]. J Differ Equations,1987,67:199-211.

[10] MA W,MINDA D. A unified treatment of some special classes of univalent functions[C]∥LI Z, REN F, YANG L. Proceedngs of the Conference on Complex Analysis.Cambridge,Massachusetts:International Press,1994:157-169.

Keywords： analytic functions; inclusion relations; coefficient estimates; Fekete-Szegö inequality.

【责任编辑 庄晓琼】

PROPERTIESANDCHARACTERISTICSOFCERTAINSUBCLASSOFANALYTICFUNCTIONS

LIU Zhiwen, LIU Mingsheng

(School of Mathematics, South China Normal University,Guangzhou 510631,China)

Some interesting properties of a subclassMn(α,β) of analytic functions are investigated. Several inclusion relations, coefficient estimates, Fekete-Szegö inequality are proven here for this function class.

2009-04-28

国家教育委员会博士点基金资助项目(20050574002)

刘志文(1985—)，男，江西瑞金人，华南师范大学2007 级硕士研究生，Email: liuziwen1985@163.com；刘名生(1965—)，男, 江西大余人, 博士, 华南师范大学教授，主要研究方向：复分析,Email:liumsh@scnu.edu.cn.

*通讯作者

1000-5463(2010)03-0011-04

O174.51

A