振动力学和波动力学的讨论

胡世丽,李贵荣

(江西理工大学, 江西赣州市 341000)

振动力学和波动力学的讨论

胡世丽,李贵荣

(江西理工大学, 江西赣州市 341000)

振动力学和波动力学是动力学的两个分支,作为动力学的两种研究方法,既有密切的联系,也有明显的区别,振动力学反映的是结构体的整体振动,体现了能量在结构体内部的转换,波动力学反映的是能量的传播。从概念、建立方程、求解方程和适用范围多个方面阐述了两者的区别和联系。

振动力学;波动力学;地震波;适用范围

振动力学研究结构的振动;波动力学研究波的传播,可以用位移、应力或应变等物理量来描述。这里有一个重要的问题,就是质点的振动,质点的振动是振动力学研究问题的起点,波动力学建立波动方程时,是从介质内取出一个单元,这单元也经常被看成质点,因此也可以是波动力学研究问题的起点,思考复杂问题时的一个简单模型,所以质点振动是一个特殊的振动力学问题。

1 冲击载荷在结构体中的传播过程

在结构体未受到扰动之前,质点之间的相互作用力处于平衡状态,一个冲击载荷作用于一个结构内的某一局部或某一质点时,受到冲击载荷作用的质点就要偏离原来的平衡位置而进入运动状态,这个质点发生振动,但冲击载荷并不能立即引起结构体内所有质点的振动,而是振动按照介质的波速在介质内传播,振动在介质内传播一段时间后,就会引起很多质点的振动,直至所有质点都振动起来。很多质点的振动就形成了一个振动场,称之为波场,质点的振动可以用位移、速度、应力、应变等物理量来描述,就形成了相应的波场,如位移波、速度波等。以位移波为例,位移波在结构体内传播过程中,遇到结构体的边界时会发生反射和透射,位移波在结构体内多次透射和反射就会形成一些特征频率,特征频率的形成主要受结构体的材料参数、结构和边界条件的影响。

一般来说,结构体内每个质点的振动都有很多个特征频率,各质点的特征频率并不完全相同,如果各质点有共同的特征频率,结构体就能形成稳定的振型(也称为模态)。

2 数学方法

结构振动力学方程和波动方程,从根本上说两个方程是一致的,都是惯性力等于不平衡弹性力,但是两者方程的推导过程和求解过程存在区别。

2.1 推导方程的过程

结构振动力学方程的推导过程是,写出结构体的总动能和总势能,把总动能和总势能代入拉格朗日方程就求出了振动方程[1]:

式中,M为质量矩阵;q为广义坐标列阵;K为刚度矩阵;Q为非保守力列阵。

从方程的推导过程可以看出,振动力学把结构体看成是一个整体,因此结构体内各质点间的相互作用力就属于内力,振动方程反映系统内部动能和势能的相互转换。

波动方程的推导过程是,在介质内部取出一个单元体,在波的传播过程中,分别写出单元体受到的不平衡弹性力和惯性力,代入牛顿第二定律方程,再代入几何方程和本构方程,就可得到波动方程,一维纵波方程推导的结果为:

式中,u、t、E和ρ分别为位移、时间、介质的弹性模量和密度;x表示波的传播方向。

单元体受到的不平衡弹性力是周围单元体和该单元体的相互作用力,周围单元对该单元的力属于该单元的外力,因此波动方程反映的是单元体间的相互关系,能够体现传播特性,实际上应力波在弹性体中传播时,不是一个动能和势能相互转换的过程,是一个能量传播的过程。

2.2 求解过程

在对方程求解时数学处理也有所不同,以一维问题为例。振动力学考虑问题时主要是从振型(或模态)入手,所以振动力学解的基本形式是:

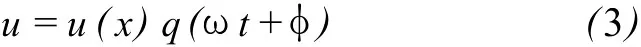
式中,u为x处的位移;ω为角频率;φ为初相位。u(x)是振型,从解的基本形式u(x)q(ωt+φ)可以认为是振型的振动,即结构的整体振动,反映了振动力学关心的是整体。如果考虑多级振型,就采用累加的方法来处理,即:

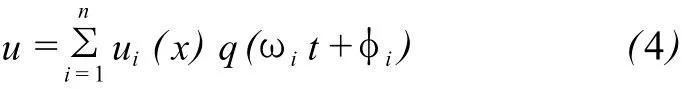
对于一个确定的x,问题就转化为质点振动问题,如果是考虑多级振型,就变成一个多频率的复杂质点振动问题。振动力学不太考虑复杂结构的瞬态振动,只考虑稳态振动,因为瞬态振动没有稳定的振型,这是振动力学本身的缺陷,如果要考虑高级振型,振动力学的解法非常困难,但实际上很多工程问题不需要考虑高级振型,低级振型的振幅大,所占能量比重大,是结构整体破坏的根本原因,因此工程问题只考虑几个低级振型。瞬态振动是一个应力波在结构中传播的过程,还会形成稳定的振型,如果外载荷恒定,应力波在边界多次反射后,结构中各个质点就会形成一些共同具有的特征频率,这就形成了振型。

波动力学考虑波的传播过程,能把波传播过程带来的各种现象展现出来,所以数学处理时就要体现传播过程,因此方程的解写成:

式中,A0为振幅;k为波数。式(5)是波向x的正方向传播的基本解,从解的基本形式可以看出,(kxωt)是波的相位,体现波的传播弹性,即时间和空间距离的关系。

波动方程建立后,由边界条件和初始条件确定传播特性,边界条件是波动力学问题中非常重要的。对于一个确定的x,问题也转化为质点振动问题,因此质点的振动是联系结构振动和波动的桥梁,是一个特殊的振动力学问题。

其实两种数学处理过程也有一定的联系,前者采用变量分离的形式,后者非分离变量形式。

3 适用范围

前面的分析表明:振动力学反映的是结构体的整体振动,体现了能量在结构体内部的转换,波动力学反映的是能量的传播,在实际应用过程中,主要根据这个特点来选择理论。对某个特定的动力响应过程,解的形式的选择,要视实际问题的需要来确定。这既取决于扰动源的性质,又取决于所考虑物体的相对尺寸,同时还与研究者所关心的问题等诸因素有关[2,3]。实际应用过程中可以从以下几个方面来考虑。

3.1 整体破坏与局部破坏

地震载荷作用下形成的地震波在山体内传播,一般来说,地震波不会造成整个山体破坏,山体破坏就属于局部破坏,应该选择波动力学的方法来处理问题。地震载荷作用下,房屋的振动最主要的特点是整体运动,经常造成房屋结构的整体破坏,因此就应该选择用振动力学的方法来解决问题。

3.2 有效振型

如果不能写出有效振型,那就只能是波动力学问题。对于半无限体,厚大尺寸的结构体来说,由于尺寸很大,波从加载处传播至结构体最远边界需要较长的时间,这就导致加载处的质点已经振动了很多个周期后才能传播至最远边界,使结构体很难形成稳定的振型,要使山体形成稳定的振型需要很长的时间,地震荷载作用时间不可能达到这么长;另一方面很难形成非常突出的整体运动,整体运动相对局部运动来说,是可以忽略的,因此就很难写出有效的振型。

3.3 受力形式

如果结构体是整体受力或结构体大部分面积受力,就应该是一个振动力学问题;如果局部受力,且能够写出有效的振型,也可以考虑为振动力学问题,也可以考虑为波动力学问题。比如,高层建筑物在风载荷作用的动力现象和破坏问题,这是一个结构振动力学问题,其原因是建筑物的受力面积大,建筑物的整体振动是动力现象的主要问题,风载荷引起的波动现象很微弱。

[1]刘延柱.振动力学[M].北京:高等教育出版社,1998.

[2]杨桂通.弹性动力学[M].北京:中国铁道出版社,1988.

[3]郭学彬,肖正学,张志呈,等.层状岩体爆破地震效应的测试[J].矿业研究与开发,2005,25(4):65-67.

2009-12-28)

胡世丽(1976-),女,讲师,主要从事岩土体力学方面的教学和研究工作,Email:wgsky010@126.com。