汽轮发电机冷却风扇的数值模拟及优化

刘全忠，宫汝志，王洪杰，魏显著

(哈尔滨工业大学 能源科学与工程学院，哈尔滨150001，liuquanzhong@hit.edu.cn)

轴流风扇是汽轮发电机空气冷却系统中最重要的部件，通过数值计算可以模拟风扇内部流场并提供整个流场的流动参数，充分认识轴流风扇内部流动规律，为改进设计提供有效可靠的依据.

Li Yimin 等通过流动可视化和数值模拟技术对轴流风扇内部的流动情况进行了研究，验证了数值计算方法的可行性［1］;文献［2-4］分别针对不同的轴流风扇进行了数值计算和实验，得到的数值计算结果与实验数据吻合较好;谷慧芳等基于CFD 计算，运用三阶样条插值方法，对影响风机性能的参数进行了优化分析，考虑了多种参数影响下的风机优化问题［5］;文献［6］提出了一种结合CFD 计算优化三维轴流风扇叶片的综合方法，该方法借助CFD 方法对叶片性能进行分析预测，然后对叶片进行改进.万福通过CFD 方法对轴流通风机叶片的流场进行了虚拟样机的数值模拟，得到了流场的特性参数，提出了对叶型的改进设计方案并实验验证了方案的可行性［7］;郑剑飞对低压大流量通风机内部流场进行了三维数值模拟，分析了叶片不同周向弯曲对其气动性能产生影响的原因，并提出降低其通流损失是降低通风机内部流动损失的一个有效办法［8］;齐学义等依据CFD 结果对水轮机转轮叶片由翼展中部至轮缘处的翼型进行优化，遵循三阶贝塞尔曲线的规律进行修型并增大叶片安放角，修型后的转轮经模拟计算结果表明其效率有较大提高［9］.

本文采用数值模拟分析方法，用Fluent 软件对某汽轮发电机通风冷却风扇在流量为25 m3/s工况的流场进行了数值模拟，了解其内部流场分布情况;以三阶贝塞尔曲线为叶片型线约束，通过改变叶片安放角和叶片扭转角来获取风扇性能与叶片安放角和叶片扭转角的变化规律，以效率最高点附近的叶片参数进行修型并通过CFD 验证，通过修型使轴流风扇的效率得到了明显提高.

1 理论计算方法

选取有应用背景的优秀原型叶片是轴流风机的CFD 优化设计的关键，本文研究的原始模型由哈尔滨大电机研究所提供，转动部件包括风扇叶片和前导叶，如图1 所示.

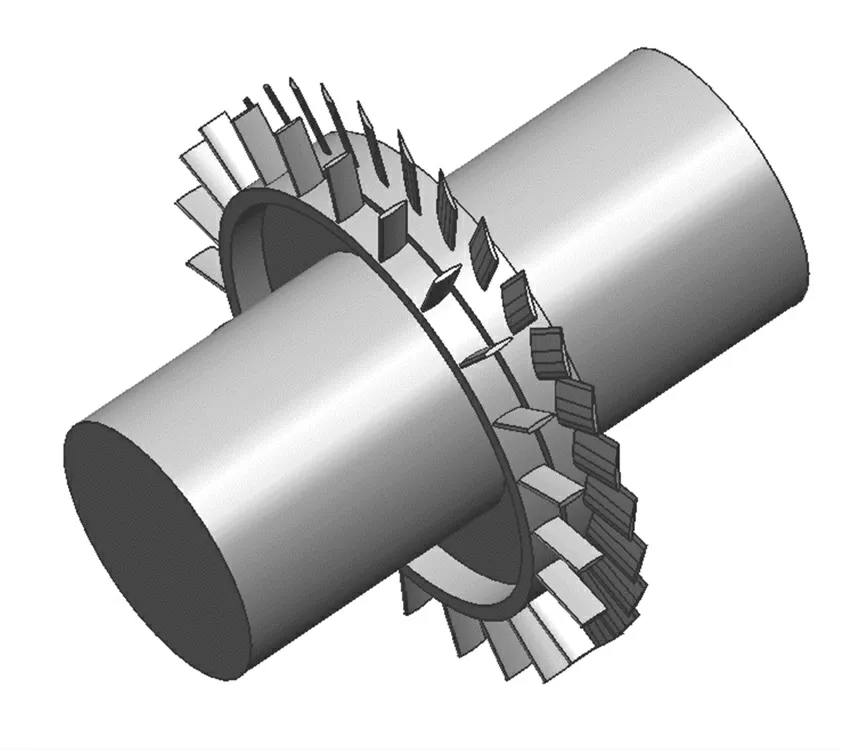
图1 轴流风扇初始几何模型转动部分

初始模型叶片尺寸和运行条件见表1.

表1 初始模型尺寸和运行条件

1.1 计算区域定义

本文计算区域为包括风扇进口段、导叶段、叶轮段和出口段在内的主流区域(如图2 所示)，采用适用性强的非结构化四面体网格划分技术，针对叶轮部分空间复杂的特点，采用网格大小为10划分网格，进口段和出口段采用尺寸函数(Size Function)由叶轮区域到边界网格逐渐变疏划分网格，网格总数为125×104，各部分网格数统计如表2 所示.

针对轴流风扇内部三维粘性湍流的流动特点，本文采用不可压缩流体雷诺平均N-S 方程:

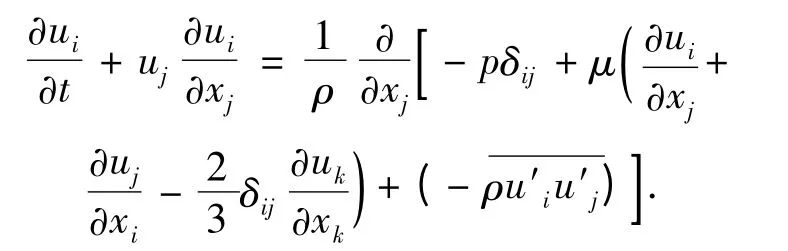
图2 计算模型示意图

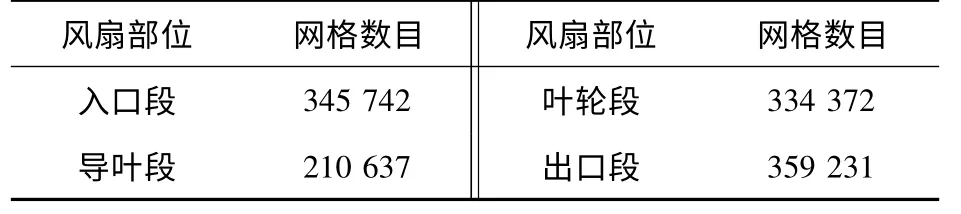
表2 各部分网格数统计

1.2 控制方程及边界条件确定

采用标准k-ε 湍流模型和连续性方程使雷诺平均方程封闭，该模型对求解有较大曲率半径的风扇内部流动有较好的适应性［10］.

使用速度入口及压力出口边界条件.采用多参考系(MRF)模型进行计算，进口与叶轮间、叶轮与出口间的界面设置为Interface(交界面)，叶轮段转动速度为3 000 r/min，应用壁面函数求解近壁区域的低雷诺数流动.

1.3 效率计算方法

风扇的效率为

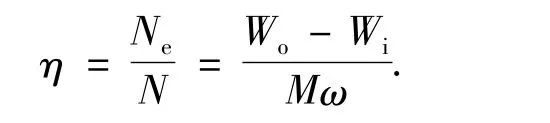
其中:η 为效率，N 为轴功率，Ne为风扇输出功率，Wi和Wo为进、出口流体具有的机械能，M 为输出转矩，ω 为风扇叶轮转速.

用User Defined Function(用户自定义函数)访问求解器，编写程序对求解器中的数据进行处理.求解器中包含风扇进出口每一个网格节点上的压力和流量值，对二者的乘积进行累加，即可求得进、出口流体具有的机械能.

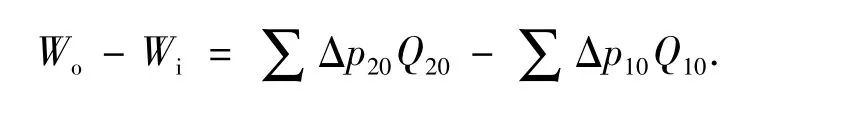
2 计算结果及优化

对原始模型风扇叶片进行优化设计，首先要获取原始风扇模型的流场参数并计算出数值效率，在此基础上，通过调整叶片参数来改善风扇内部流动特性，本文中这样的叶片参数包括叶片安放角和叶片扭转角.计算不同的叶片安放角和叶片扭转角下的风扇流场，得到效率和叶片安放角及叶片扭转角的关系，找出效率最高点对应的叶片安放角和叶片扭转角作为最终优化风扇模型.

2.1 原模型风扇计算结果

图3(a)是原始模型叶片工作面和背压面的压力分布图.从图上可以看出叶片工作面入口部分压力梯度较大(图3 中各组叶片压力分布图中由左至右分别对应从叶片入口到叶片出口)，说明在此处有流体的突然折转及撞击现象，原始模型安放角度不适合当前工况;叶片背面低压区范围较小，最低压力较低，即在较小的降压范围出现较大的压力降低，流动状态不佳;从图4(a)叶片周围的流线分布也可以看到叶片尾部有较严重的流动分离现象，导致能量损失，效率下降.用1.3中的方法对原型叶片效率进行计算发现，其计算效率为54.3%.

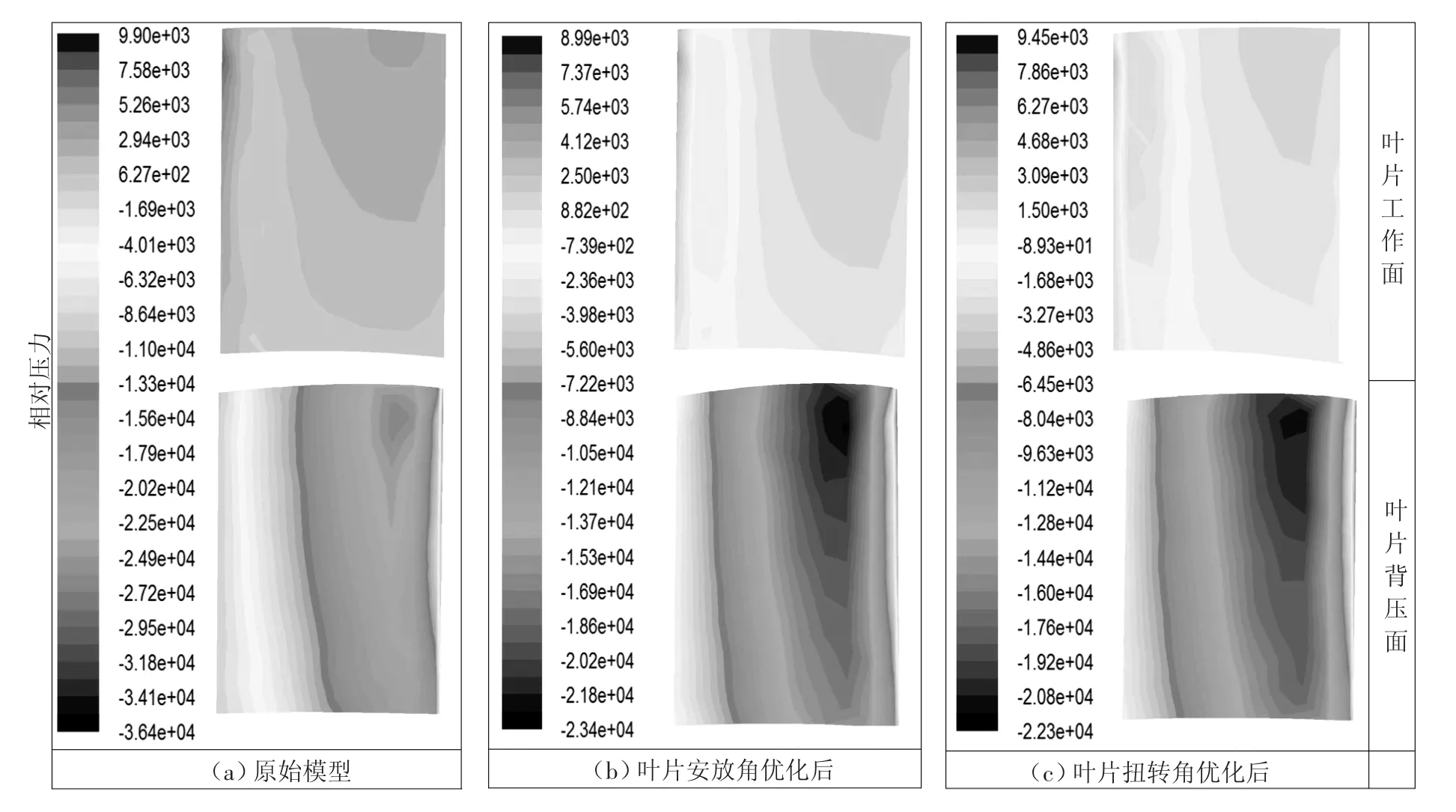
图3 叶片表面压力分布

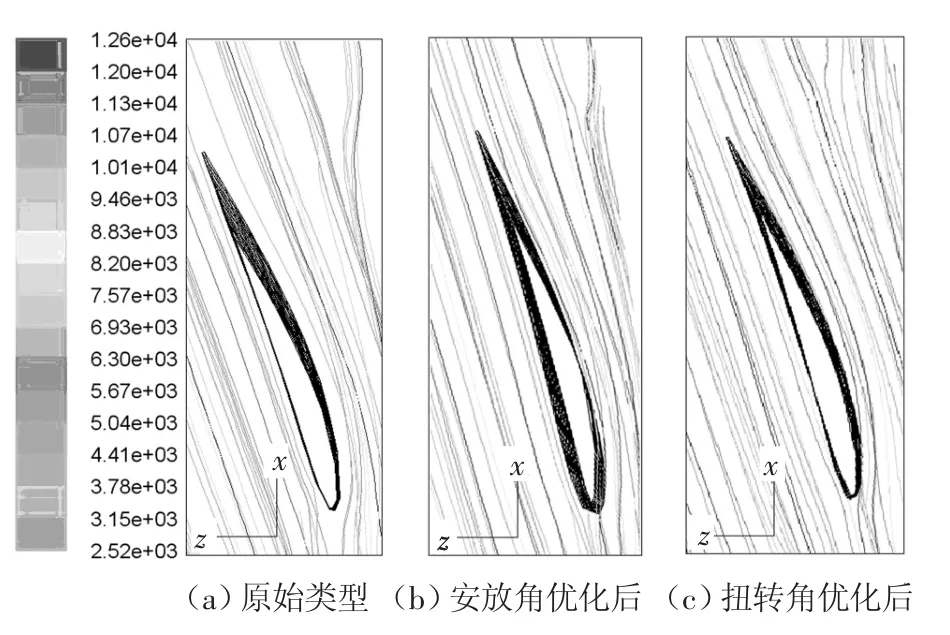
图4 叶片周围流线分布

2.2 叶片安放角的调整

图3 (a)显示在叶片工作面叶片入口位置有流动撞击现象，据此应调小叶片安放角.从20.5°到12.5°的范围内每调小0.5°计算一次流场及效率，得到效率随叶片安放角的变化规律如图5 所示.从图5 中可以看出，风扇效率随叶片安放角变化规律为先增后减，在叶片安放角约为14.5°时风扇效率达到最大值，最大效率为69.1%，此时叶片工作面和背压面的压力分布图如图3(b)所示，叶片工作面上压力梯度较原始模型更为均匀;叶片背压面低压范围扩大且最低压力较原始模型有所提高，流体沿叶片背面的流动性能得到改善.从图4(b)叶片周围流线分布也可以看到叶片表面流动分离现象减轻.

2.3 叶片的扭转

采用叶片角为14.5°时的风扇叶片继续对叶片扭转角进行优化.以叶片的中间为基准，每隔0.2°对叶片进行扭转，对每个扭转角对应的风扇叶片计算了其流场及效率，得出效率随叶片扭转角的变化规律如图6 所示，从图6 中可以看出:风扇效率随叶片扭转角变化规律为先增后减.从叶片底部到叶片顶部共扭转2.2°左右时，叶片效率可达到70.1%.叶片扭转2.2°时，由图3(c)看到叶片背面最低压力已提高到-2.5×10-3，由图4(c)可以看到叶片表面流动分离问题进一步改善.

通过以上计算，本文选取叶片安放角为14.5°和叶片扭转角为2.2°时的风扇叶片作为最终优化叶片.

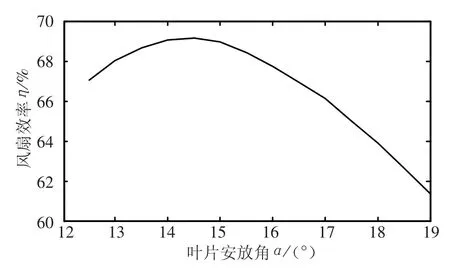
图5 风扇效率随叶片安放角的变化情况

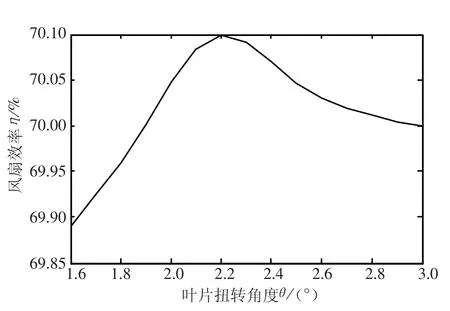
图6 风扇效率随叶片扭转角度的变化情况

3 结 论

1)对叶片安放角进行调整，并对叶片进行扭转，使轴流风扇叶轮效率由初始模型的54.3%提高到70.1%;

2)对初始风扇模型进行调整，风扇内部流体流动状况得到明显改善，叶片表面压力梯度变均匀，叶片背面最低压力由初始模型的-3.64×10-3提高到-2.23×10-3(相对压强);

3)叶片调整后，其叶片表面流动状况得到明显改善，流动分离现象得到有效控制.

［1］LI Yimin，ZHOU Zhongning.Investigation and numerical simulation of inner-flow of an axial mine-flow fan under low flow rate conditions［J］.Journal of China University of Mining＆Technology，2008，18:107-111.

［2］HOTCHKISS P J，MEYER C J.Numerical investigation into the effect of cross-flow on the performance of axial flow fans in forced draught air-cooled heat exchangers［J］.Applied Thermal Engineering，2006，26:200-208.

［3］YOUNG J M，YONG C.Computation of unsteady viscous flow and aero-acoustic noise of cross-flow fans［J］.Computers-Fluids，2003，32(7):995-1015.

［4］MEYER C J，KRIGER D G.Numerical simulation of the flow field in the vicinity of an axial flow fan［J］.International Journal for Numerical Methods in Fluids，2001，36:947-969.

［5］谷慧芳，顾平道.轴流通风机内部结构优化方法的研究［J］.风机技术，2008，12(3):20-24.

［6］LIN B J，HUNG C I.An optimal design of axial-flow fan blades by the machining method and an artificial neural network［J］.Journal of Mechanical Engineering Science，2002，216(3):367-376.

［7］万福.基于CFD 的轴流通风机叶片的流场分析与改进设计［J］.风机技术，2008(2):21-25.

［8］郑剑飞.小型轴流通风机中叶片周向弯曲影响气动性能的数值模拟［J］.风机技术，2008(2):9-12.

［9］齐学义.基于流场计算的贯流式水轮机叶片修型［J］.兰州理工大学学报，2008，34(5):45-49.

［10］SPECZIALEC G，THANGAM S.Analysis of an RNG based turbulence model for separated flows［J］.Engineering Science，1992，30(10):1379-1388.