空间域减法聚类粒子滤波算法

赵玲玲，马培军，苏小红

(哈尔滨工业大学 计算机科学与技术学院，哈尔滨150001，zhaolinglinghit@126.com)

由于很难从后验分布p(xt|z1:t)中直接抽取样本，所以一般选择一个重要性函数π(x|z)来

粒子滤波(Particle filter，PF)［1］是一种蒙特卡罗框架下的递归贝叶斯滤波技术，因为其不受线性系统和高斯噪声的限制，被广泛应用于定位导航、目标跟踪、数据处理、模式识别等领域［2］.但是，粒子滤波精度依赖于粒子数目，计算负担较大.针对这一问题，Hong 等［3-6］提出一种多分辨分析粒子滤波，该方法把小波分析引入到粒子滤波领域来，在时间域和空间域两个方面进行了研究，都取得了成功.时间域主要针对多速率系统状态估计问题;在空间域中，通过对样本集及其对应的权重进行小波分解，在粗尺度上进行阈值处理，把空间中分布相近的多个粒子用其中一个代替，有效的降低了总粒子数目，同时保持了粒子滤波的估计精度和稳定性等性能.

针对粒子滤波计算效率问题，受多分辨分析在粒子滤波中的应用的启发，采用聚类［7-8］方法代替多分辨分析来处理空间域中的样本集，通过把空间特征和权重分布相近的粒子进行聚合，来降低总的样本数，达到提高计算效率的目的.这一方法不受状态维数的限制，不需预先对样本进行排序，经过聚合处理后的样本，一方面仍然保持着状态的后验分布的几何特征，另一方面，在状态空间中进行传播的粒子显著减少，计算效率明显提高.同时，粒子数目也可以通过设定合理的阈值(聚类半径)进行自适应的调节.

1 一般粒子滤波算法

对于非线性滤波问题，其状态空间模型为

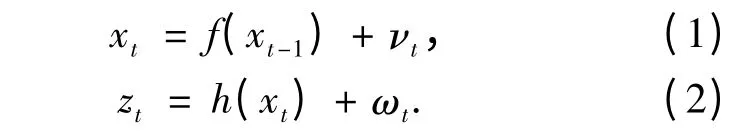
式中:xt∈Rnx为t 时刻的状态向量，zt∈Rnz为传感器在t 时刻得到的测量向量，νt∈Rnv和ωt∈Rnw分别为独立同分布的过程噪声向量序列和观测噪声序列，ft:Rnx×Rnv→Rnx为状态转移函数，ht:Rnx×Rnw→Rnz为该传感器的量测函数.

粒子滤波通过寻找一组在状态空间Rnx中传播的加权随机样本的方法来对近似后验概率密度函数p(xt|z1:t)，算法首先计算预测概率密度，然后更新后验概率密度.生成样本集.这就是重要性采样过程，则后验概率密度为

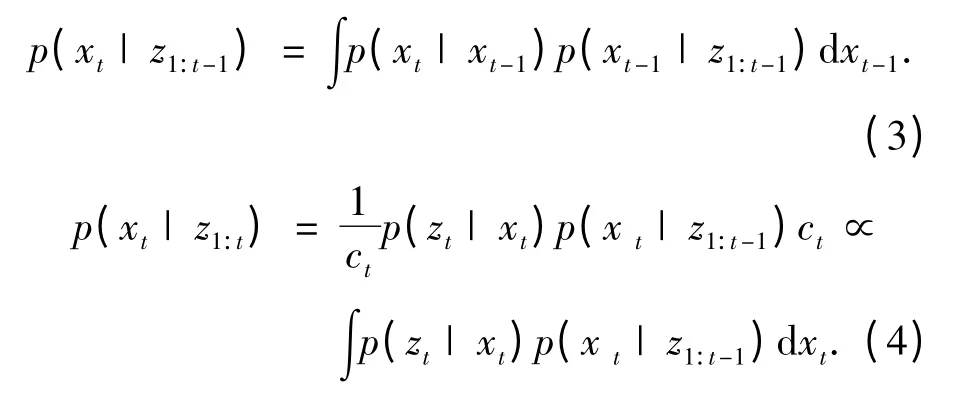
由于很难从后验分布p(xt|z1:t)中直接抽取样本，所以一般选择一个重要性函数π(x|z)来

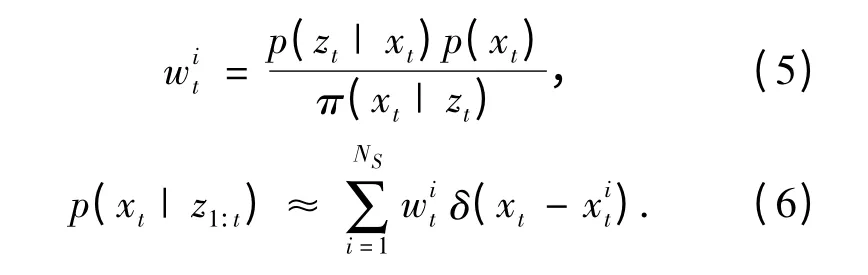
2 空间域减法聚类粒子滤波

聚类是一种将样本空间中的元素按某种相似性度量划分为若干个子类的过程.本文将聚类算法用于粒子滤波中对带权粒子集的处理，而这些粒子具有明显的动态性，因此无法预先确定分类个数.另外，选取的聚类算法应具有较高的计算效率，综合这些因素，采用减法聚类来处理样本集，并根据样本集描述后验概率密度时的几何特点，对减法聚类进行了改进.

2.1 改进的减法聚类算法

减法聚类［9-10］是一种基于密度的聚类算法，其计算复杂度与样本维数无关.

假设聚类对象为M 维状态空间中的n 个样本{x1，x2，…，xn}，初始阶段先计算所有样本处的密度:

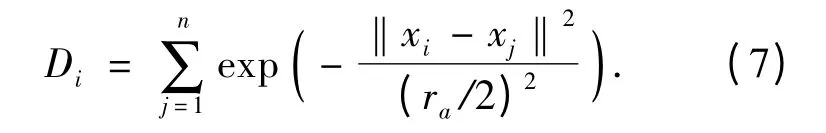
然后选择密度最大的点xC1作为第一个聚类中心，修正剩余点的密度:

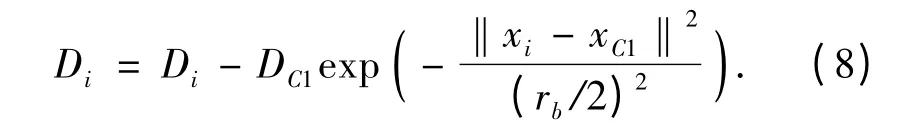
式中:DC1为xC1处的密度，ra和rb分别为常数，一般满足rb＞ra，以避免聚类中心距离过近.

当满足预设条件后，现有的减法聚类算法对剩余样本不做处理，这些样本的密度低于其他样本，因此认为其不可能成为聚类中心.但是，在粒子滤波中，对于经过权重更新后的样本集，由于其空间分布具有一定的随机性，因此某些低密度处的粒子，可能表征着后验分布中比较重要的特征，丢弃后可能导致部分后验分布特征的丢失，进而导致估计精度的下降，因此对低密度空间域中的样本都予以保留，以确保描述后验分布的关键点的完整性.

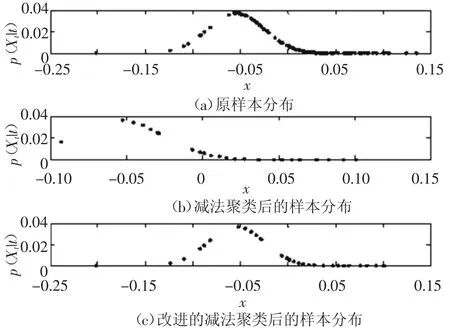
图1 聚类前后的样本分布对比

2.2 基于改进减法聚类的粒子滤波

定义 如果样本xi和xj满足‖xi-xj‖≤r，且|wi-wj|≤ω，即认为xi和xj相似.其中，wi和wj分别为xi和xj对应的权重，r 和ω 分别为预设的常数.

根据这一定义，可知聚类数据点(向量)的构造不能单纯使用样本集，而是应该将和予以结合，即不能只根据样本的空间分布对其进行聚类，因为即使空间位置非常相近的样本，其权重也可能相差较大，这种现象在后验分布比较尖锐时尤其明显.基于这一考虑，采用下述方法来构造聚类向量:

2)根据预设的聚类半径rs，采用改进后的减法聚类算法对构造好的向量集进行处理，得到聚类中心集合，其中，nt为聚类个数.对ct进行逆映射得到:，其中，i =1，…，nt;g:Rnx×R →Rnx+1;g-1为相应的逆函数.再对权重进行归一化处理，这样就获得了新样本集和对应权重，完成了一次滤波过程.本文将根据这一思想实现的算法称为基于聚类的粒子滤波算法(Cluster-based Particle Filter，CPF).图2 是CPF 算法的原理图.

图2 中构造聚类向量、聚类、分解聚类向量，输出新样本集和权重的过程就是聚合过程.经过聚合过程，原样本集数量降低，而其表征的后验分布的基本特征不变.

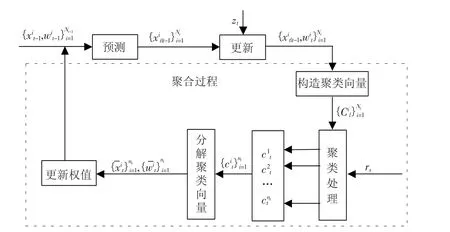
图2 CPF 算法原理框图

3 仿真实验及分析

3.1 线性高斯模型

设定状态空间模型:

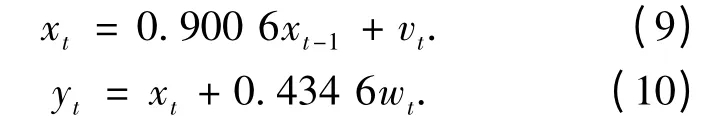
表1 为100 次仿真实验的平均运行结果.图3为PF(1)与CPF 算法的单次运行结果的估计性能比较.

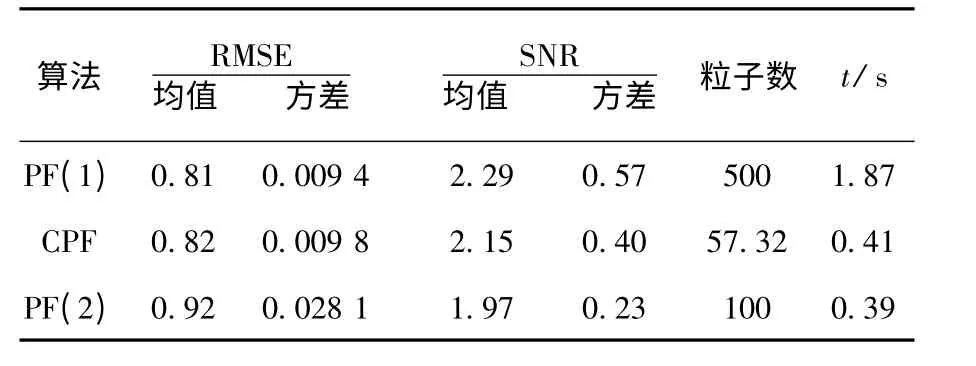
表1 PF 与CPF 算法性能比较

由表1 可以看出，初始样本数为500 的CPF，其估计精度与样本数为500 的PF(1)算法相当，但计算效率明显提高，其原因是CPF 在整个运行过程中的平均样本数目约为57，显著低于一般PF算法，因此比PF 算法更为有效.

同时，与样本数为100 的PF(2)算法相比，CPF 的运算时间略高于PF(2)，但前者的估计精度明显高于后者，说明了聚合过程保留的样本比一般粒子滤波中的分布带有一定随机性的样本在描述后验分布时更为有效，聚合过程达到了对样本进行优选的目的.

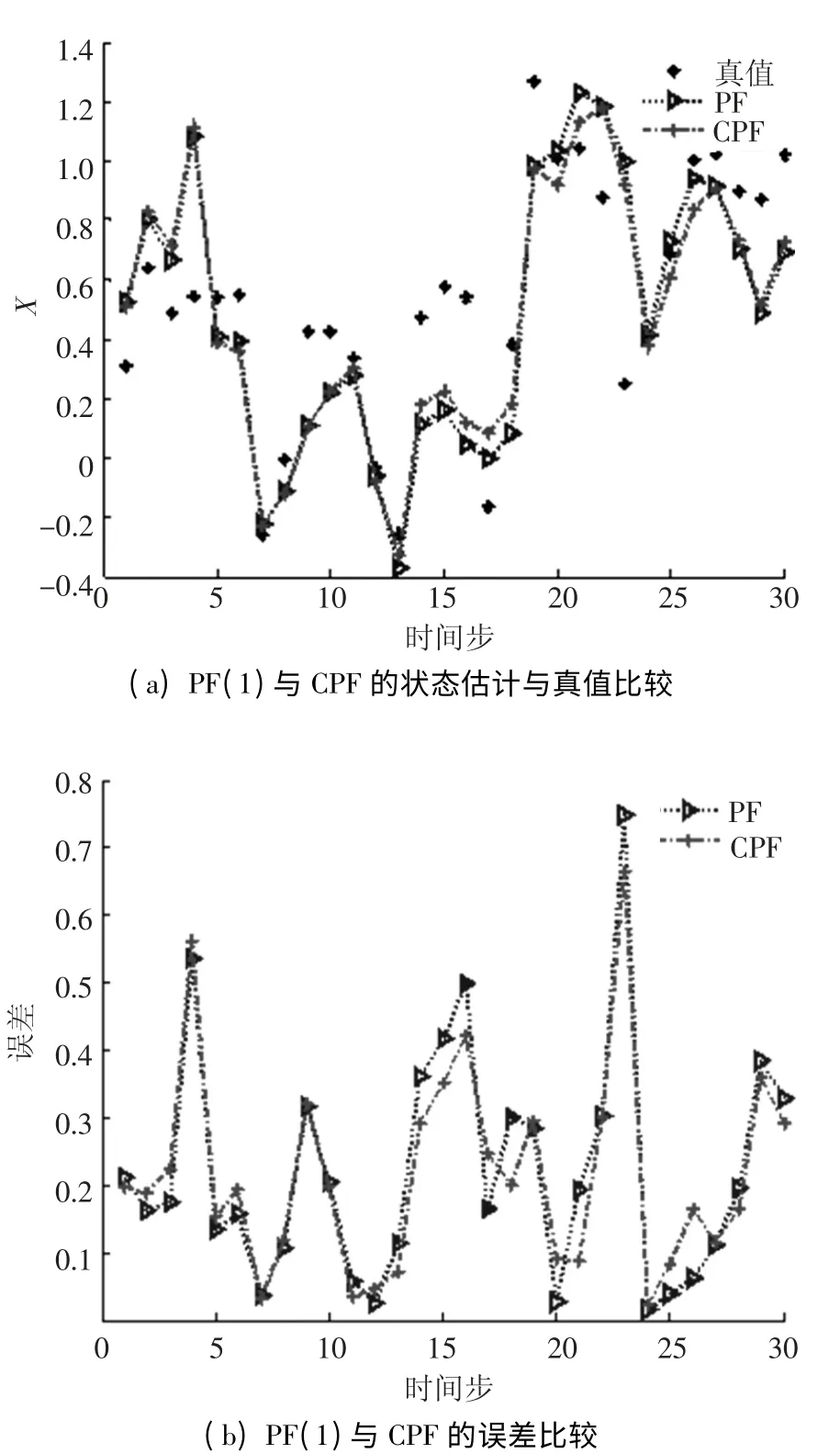
图3 PF(1)与CPF 的估计性能比较

由图3 可以看出，初始样本数相同的PF 和CPF 算法，在这个算法的执行过程中，CPF 的样本数目虽然在不断降低，但两者估计曲线和误差曲线都基本吻合，说明了样本数目的减少并未影响CPF 的估计性能.

图4 为某个状态传播周期内样本在空间中的分布情况.由图4 可知，经过聚合后的样本分布保持了原后验分布的基本特征，而存在的粒子数目大大降低了.

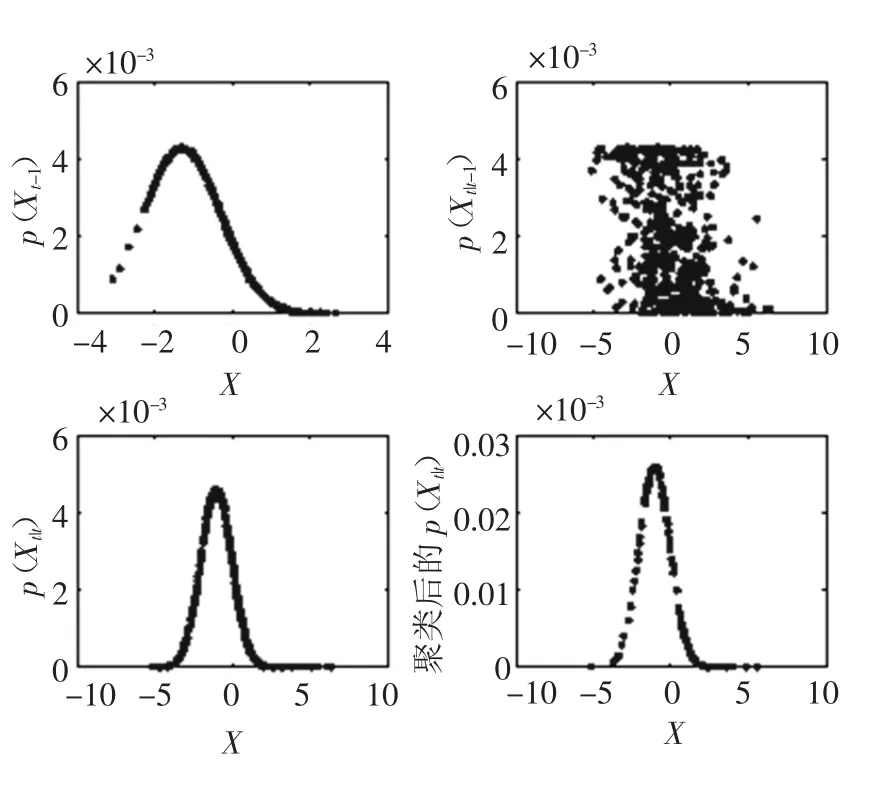
图4 CPF 算法的样本分布及对应权重

3.2 UNGM 模型

单变量非静态增长模型(Univariate Non-stationary Growth Model，UNGM)，具有典型的非线性特征，后验分布呈现双峰性.其状态空间方程为

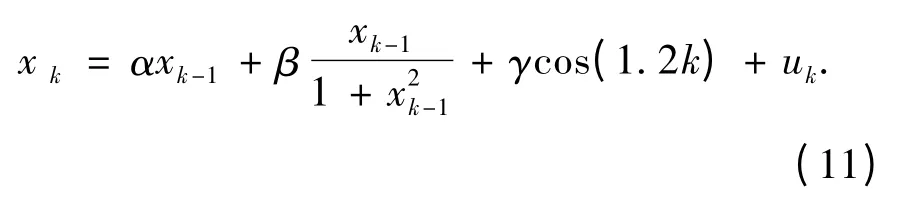
测量方程为

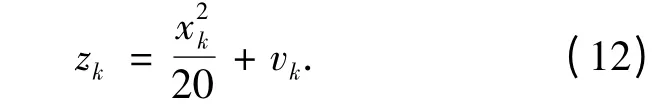
实验中针对不同的误差参数设定对算法PF和CPF 分别进行100 次仿真实验，其中，组1 中，组2 中，组3 中.令rs=0.001，实验结果如表2 所示.同时记录PF 和CPF 算法单次运行的实时估计误差，结果如图5 所示.

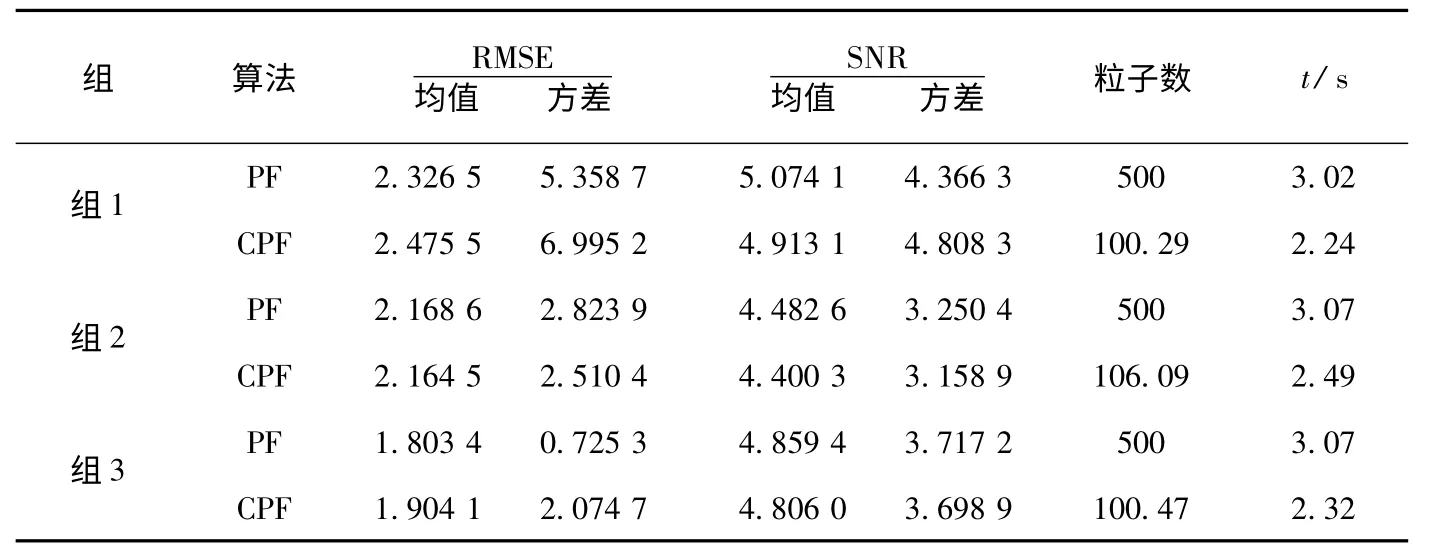
表2 PF 与CPF 算法性能比较

由表2 可以看出，在UNGM 模型下，在系统误差较大的情况下(组1)，CPF 的精度比PF 略差，稳定性也有所下降;在系统误差降低的情况下(组2 和组3)，CPF 的估计精度与一般PF 相近.CPF 的平均样本数明显低于PF，运算时间少于PF，说明CPF 算法的计算效率更高.

CPF 算法的稳定性差于PF，说明在粒子数目降低的情况下，虽然大部分的后验分布特征予以保留，但不排除多次试验过程中出现了关键点的丢失，因此引起了滤波稳定性的下降，以及平均估计精度的损失，但从发生次数的统计结果(100 次仿真中出现了6 次)来看，这种情况的发生频率较低.

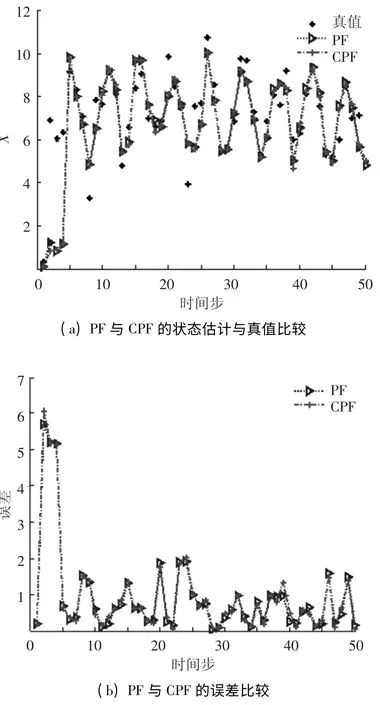
图5 PF 与CPF 的估计性能比较

4 结 论

1)提出一种在空间域中结合减法聚类来降低样本数量的粒子滤波算法，通过对样本集及其对应权重进行聚类，获取空间中根据密度及分布特征聚合而成的多个样本子集，用每个样本子集的中心代替其他样本，达到降低样本数目的同时保持后验分布基本特征不变的目的，进而降低粒子滤波的计算复杂度.

2)实验结果表明该方法基本保持了一般粒子滤波算法的估计精度，而所需的样本数明显降低，消耗的计算时间下降.

3)此外，该算法通过选择不同的聚类算法来进一步提高算法在实际应用中的计算效率.

［1］GORDON N J，SALMOND D J，SMITH A F M.Novel approach to nonlinear/non-gaussian bayesian state estimation［J］.IEEE Proceedings-F，1993，140(2):107-113.

［2］BAGDANOV A D，BIMBO A Del，DINI F，et al.Adaptive uncertainty estimation for particle filter-based trackers［C］//Proceedings of the 14th International Conference on Image Analysis and Processing.Washington DC:IEEE Computer Society，2007:331-336.

［3］HONG L，CUI N，BAKICH M，et al.Multirate interacting multiple model particle filter with application to terrain-based ground target tracking［J］.IEEE Proceedings Part D，Control Theory Applications，2006，153(6):721-731.

［4］HONG L，WICKER D.A spatial-domain multiresolutional particle filter with thresholded wavelets［J］.Signal Processing，2007，87(6):1384-1401.

［5］HONG L，XUE K F.A spatial domain multiresolutional particle filter［C］//15th Mediterranean Conference on Control and Automation.Greece:IEEE，2007:T23-008.

［6］HONG L.Multirate interacting multiple model filtering for target tracking using multirate models［J］.IEEE Transactions on Automatic Control，1999，44(7):1326-1340.

［7］DUDA R O，HART P E，STORK D G.Pattern Classification［M］.2ndEdition.New York:Wiley，2001.

［8］YAGER R R，FILEV D P.Approximate clustering via the mountain method［J］.IEEE SMC，1994，24(8):1279-1284.

［9］CHIU S L.Fuzzy model identification based on cluster estimation［J］.Journal of Intelligent and Fuzzy Systems，1994，2(3):267-278.

［10］PAL N R，CHAKRABORTY D.Mountain and subtractive clustering method:improvements and generalizations［J］.International Journal of Intelligent Systems，2000，15(4):329-341.