YX128°-LiNbO3 SAW 传感器IDT 的有限元仿真

薛齐齐，孙崇波，孙 毅

(哈尔滨工业大学 航天科学与力学系，哈尔滨150001，xueqiqi@hit.edu.cn)

SAW 器件是用来信号处理的一种微机械电子系统，它利用压电基底上的叉指换能器来激发和接收表面波.SAW 传感器是SAW 器件的一个新的重要分支，具有高精度、高分辨率、数字输出、重量轻、体积小、功耗低、抗干扰、耐噪声等独特优点［1-2］.目前，SAW 传感器已经在气体检测、无线监测及生物医疗检测等领域获得了广泛的应用.Y.Liu 和T.H.Cui 利用商业软件ANSYS 和PSPICE 分 析 了SAW 传 感 器 的 能 耗［3］.M.S.Zaghloul 等分析了液体环境下SAW 谐振器作为传感器的性能，并与实验结果做了比较［4］.V.Laude 等利用渐近线波形估计法在获得准确仿真结果的同时大大缩短了有限元/边界元仿真的时间［5］.Le Brizoual 等建立了AlN/金刚石层状表面波器件的有限元模型并分析了其性能［6］.SAW 传感器技术作为一门新兴技术，展现了巨大的发展潜力.而国内对SAW 传感器开发应用多停留在实验阶段.在以往的低频SAW 传感器模型中，由于电极厚度相对于电极宽度很小，因此假设电极厚度为零，如Delta 函数法［7］，等效电路法［8］等模型.为了追求更好的性能，SAW 传感器向着高频率的方向发展［9］.高频环境下高的电极厚度宽度比造成的二次效应则不能再忽略.另外，一些传感器参数的获得，严重地依赖于传感器原型机实验，而有限元分析可以在一定程度上代替原型机实验来提取传感器参数.本文建立了SAW 传感器IDT的有限元模型，定量地分析了不同电极参数下的电极二次效应，并计算出SAW 传感器IDT 的一些参数.

1 有限元模型

1.1 有限元方程

通过压电材料中弹性波的传播的两类方程控制，即运动方程和麦克斯韦方程，可得压电材料中的波动方程，方程将电势和位移的3 个分量耦合在一起:

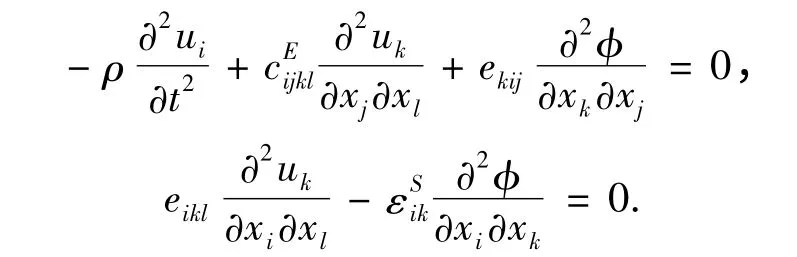
一般而言这些方程需要与描述基底材料周围介质中的电场的麦克斯韦方程一起求解.但在本文设计的气体传感器中，其工作环境为空气，其介电常数要远小于基底材料.因此，忽略空气介质，只要给介面指定恰当的电压和力边界条件，就可以对压电基底独立求解上述方程.当从变分的角度考虑时，这种假设的重要性就更明显.取

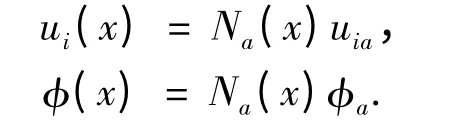
式中:uia和φa分别为单元结点的位移分量和单元结点的电势分量，Na(x)为单元形状函数，脚标a表示单元的结点号.

压电材料有限元程序的核心工作就是求解这类方程.在ANSYS 中可以选择不同的算法求解这些方程组.

1.2 周期性结构模型的建立

延迟线型SAW 传感器结构如图1 所示，在YX128°-LiNbO3压电基体上分布着一个输入叉指谐振器和一个输出叉指谐振器，叉指电极尺寸是均匀一致的，并交替连接在两条总线上.

由于计算能力的限制，无法建立全尺寸的有限元模型进行分析，本文对SAW 传感器的有限元模型做了如下简化和假设:

1)平面应变假设.当在IDT 电极上加上交变电信号时，激发出的瑞利表面波的传播方向垂直于电极声孔径方向，电极声孔径方向的位移并没有被耦合在波动方程中.考虑到电极的长度要远大于其宽度，并且忽略电极末梢的表面波偏转，对SAW 传感器应用平面应变状态假设，将其由三维模型简化为二维模型.

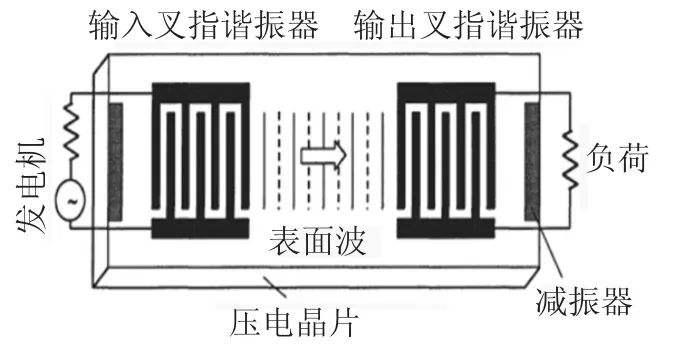
图1 SAW 传感器基本结构

2)基体深度的缩短.表面波的能量随深度增加呈指数衰减，在3 倍波长深度的地点能量衰减不足5%，利用这一特征，本文仅模拟10 倍波长的基体深度即可足够精确地模拟表面波的特性.

3)周期性结构的简化.通常，SAW 传感器IDT 的电极可达几十、几百至上千对，全部模拟计算量将非常巨大，也不现实，利用周期性边界条件可以成功地将向波传播方向两侧无限延伸的周期性结构简化为单个单元结构.更简单的模型中，半个波长的模型也可以模拟这种周期性结构，只要在左右边界加上符号相反的边界条件.本文采用单倍波长周期性结构.

简化后的周期性结构模型示意图如图2 所示，模型波长周期为4 μm，压电基体深度取40 μm，模型的周期性边界条件为

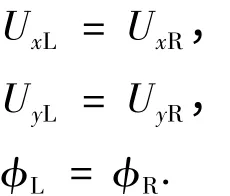
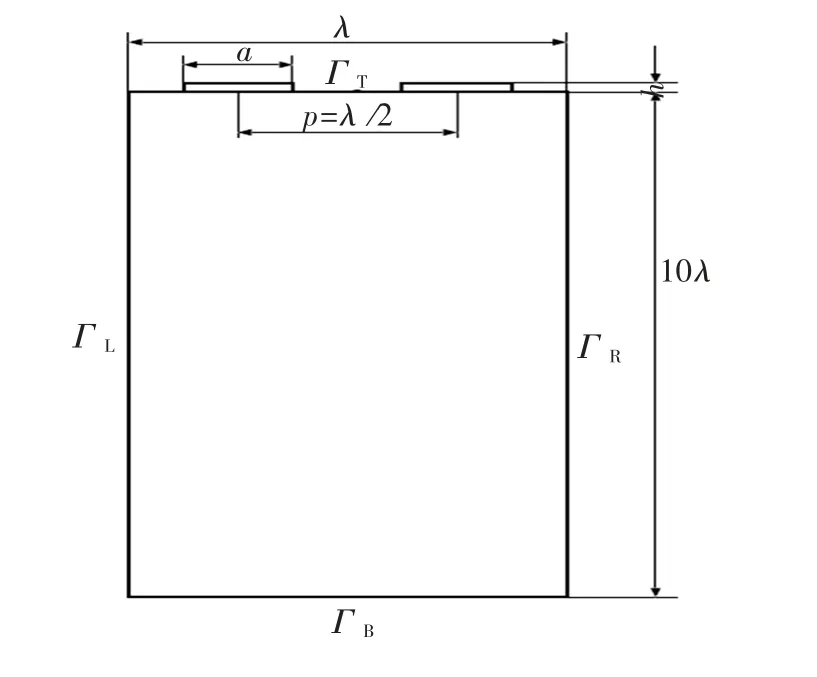
图2 SAW 传感器周期性结构示意图

模型底边的边界条件ΓB为约束位移自由度，顶边ΓT为自由边界.在ANSYS 中分网后的有限元模型如图3，为了清楚起见，图中只显示了部分模型.电极材料为铝，电极参数敷金比MR 和电极高度无量纲值EH 分别定义为

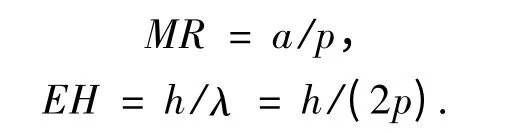
式中:a 为电极宽度，p 为电极周期间距，h 为电极绝对高度值，λ 为波长.为了定量分析不同电极参数下的电极二次效应，建立了一系列不同电极参数的有限元模型，模型的敷金比MR 由0.3 变化至0.7，EH 由2.5%变化至3.5%.

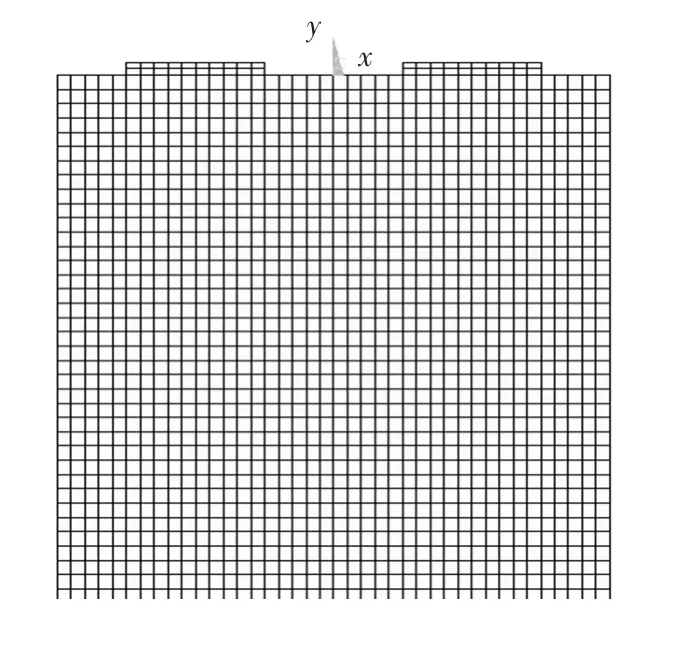
图3 分网后的有限元模型

2 分析结果与讨论

对建立的有限元模型进行模态分析，从提取的模态振型中可以分辨出有两个振型是表面波的振型.其中，振型左右边界上Y 方向的位移为零的，称为反对称模态，其特征频率记作fsc+;模态左右边界上X 方向的位移为零，称为对称模态，其特征频率记作fsc-.这两个频率构成了频率截止带的两个边界，表面波的传播速度v 和电极反射率kp可由反对称模态频率和对称模态频率确定，具体表达式为

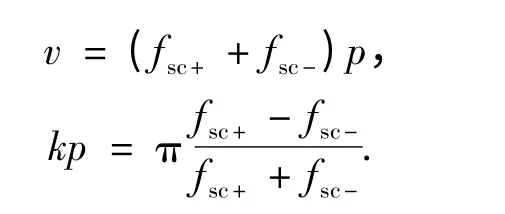
由上式可知，知道了某一电极参数对应模型的反对称模态频率和对称模态频率，便可以求得在电极质量效应影响下的表面波波速和电极反射率.因此，反对称模态频率和对称模态频率可以作为表征电极二次效应的参数.分析结果总结在表1中.对比表中波速与自由表面波速(4 000 m/s)，可知由于电极的质量效应影响，电极的存在降低了表面波的波速.由分析结果可知，随着MR 或EH 的增大，表面波的模态频率降低，相应的表面波的速度也会降低.图4 显示了表面波波速随MR 及EH 的变化关系.同时还得到了模态频率随敷金比的变化趋势，在相同EH 下，随着敷金比的增大，频率截止带逐渐变宽，对应的电极反射率逐渐变大.

模态分析只能给出模型的振型，而不能直接计算出一些物理量的具体数值.更一般的方法是响应分析.对SAW 传感器IDT 进行响应仿真的原理是:在传感器IDT 电极上施加电压载荷作为响应激励，通过计算激励产生的电流或电荷间接计算出IDT 的导纳值，电极上总的复数电荷值Q 及复导纳Y 的关系式为

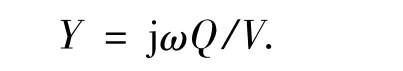
式中:Y 是复导纳，j 是单位虚数，ω 是角频率，V 是驱动电压.

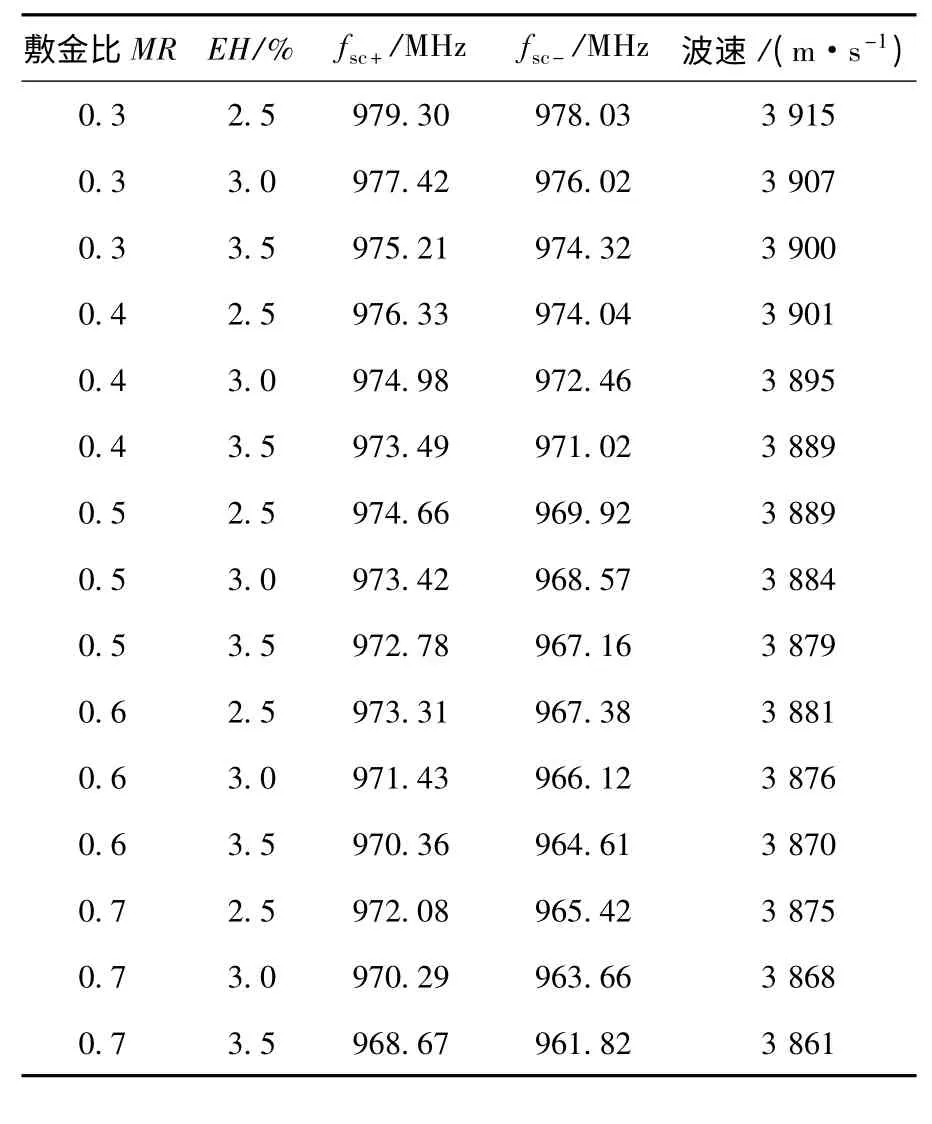
表1 电极二次效应分析结果

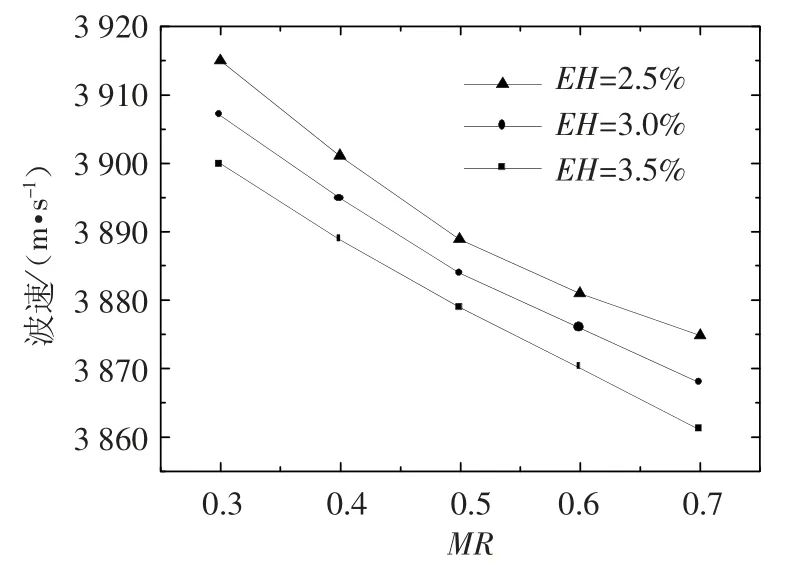
图4 表面波波速与MR 及EH 的关系

在谐响应分析中，作为激励的载荷为施加在电极上的一个简谐变化的电压±0.1 V(峰值0.2 V).载荷在模型中的具体实现过程为:耦合同一电极位置上的结点的电压自由度，使其电压值相等，然后选择一结点施加电压载荷.在分析特性中设定分析频率范围在模态分析获得的表面波特征频率附近.模型中电极的敷金比MR 和电极高度无量纲值EH 分别为0.5 和0.3%，模型的其他属性与边界条件与模态分析相同.计算得到的导纳频率关系显示在图5 中.导纳取极大值的频率点称为谐振频率，导纳取极小值的频率点称为逆谐振频率，仿真提取的谐振频率为973 MHz，逆谐振频率为1 002 MHz.

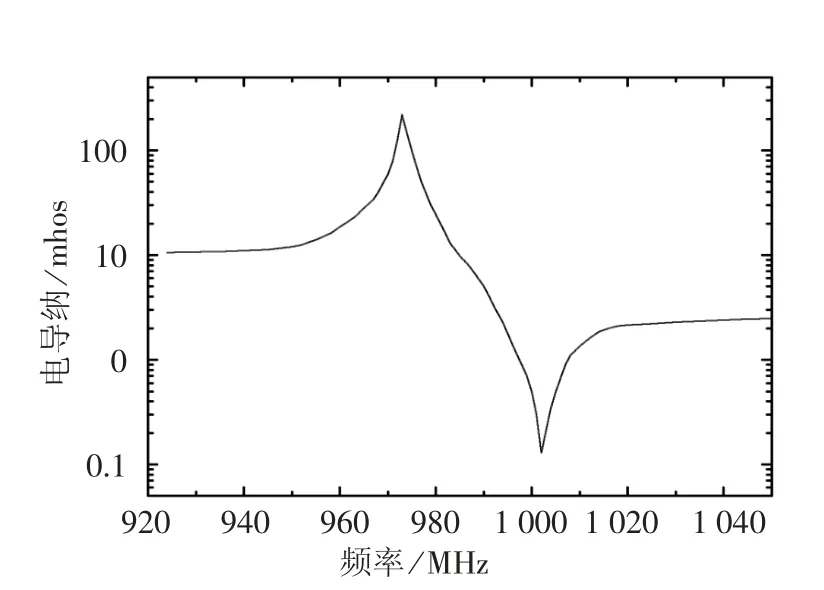
图5 传感器IDT 的电学导纳与频率关系

计算得到谐振频率时的导纳要高于100 mhos，而实际的导纳要远低于这个值，这主要是由于二维有限元模型中假设传感器声孔径是无限大的，而本文设计的SAW 气体传感器声孔径为90 倍波长，另外周期性结构模型假设电极在表面波传播方向是无限延伸的，实际的电极对数是有限的，这也会造成计算的值偏大.

3 结 论

本文应用ANSYS 建立了SAW 传感器的有限元模型.通过对不同电极敷金比MR 和电极高度无量纲值EH 的一系列模型进行模态分析，定量分析了不同电极参数下的电极的二次效应.进一步对模型进行了谐响应分析，得到了传感器的电学导纳随频率的变化规律，提取了SAW 传感器IDT 的谐振频率和逆谐振频率.利用有限元可以代替原型机实验，大大减少实验量，缩短传感器开发周期，降低开发成本.仿真结果还可以为整个传感器系统进一步的设计提供重要的参考.

［1］BENES E，GROSCHL M，BURGER W，et al.Sensors based on piezoelectric resonators［J］.Sensors and Actuators:A，1995，48(1):1-21.

［2］WOLFF U，DICKERT F L，FISCHERAUER G K，et al.SAW sensors for harsh environments［J］，IEEE Sensors Journal，2001，1(1):4-13.

［3］LIU Y，CUI T H.Power consumption analysis of surface acoustic wave sensor systems using ANSYS and PSPICE［J］.Microsystem Technologies，2007，13(1):97-101.

［4］ZAGHLOUL M S，TAHA T E，MOUSTAFA A H A，et al.Modeling and simulation of fluid SAW-sensors under acoustic plate mode operation［J］.IEEE Transactions on Instrumentation and Measurement，2001，50(1):95-100.

［5］LAUDE V，REINHARDT A，WILM M，et al.Fast FEM/BEM simulation of SAW devices via asymptotic waveform evaluation［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2004，51(3):359-363.

［6］LE BRIZOUAL L，ELMAZRIA O.FEM modeling of AlN/diamond surface acoustic waves device［J］.Diamond and Related Materials，2007，16(4-7):987-990.

［7］TANCRELL R H，HOLLAND M G.Acoustic surface wave filters［J］.Proceedings of the IEEE，1971:393-409.

［8］SMITH W R，GERARD H M，COLLINS J H，et al.Analysis of interdigital surface wave transducers by use of an equivalent circuit model［J］.IEEE Transaction on Microwave Theory and Techniques，1969，MTT-17(11):856-864.

［9］WHITE R M.Acoustic sensors for physical，chemical，and biochemical Applications［C］//IEEE International Frequency Control Symposium.Pasadena:［s.n.］，1998:587-594.