基于实物期权理论的露天采矿边际品位最优化
郝全明,罗业民
(内蒙古科技大学矿业工程学院,内蒙古包头 014010)
基于实物期权理论的露天采矿边际品位最优化
郝全明,罗业民
(内蒙古科技大学矿业工程学院,内蒙古包头 014010)
以实现矿山利润最大化为目的,借助金融学里的实物期权理论建立了露天采矿边际品位最优化数学模型,并以一个案例验证了所建模型的优越性,为矿山开采品位决策提供了新途径。
边际品位;实物期权;最优化数字模型
矿石品位的高低是采矿业管理中一个重要的决策问题。露天矿边际品位在露天矿生产的过程中处于非常重要的地位,它关系到露天矿的可采矿量、剥岩量、生产能力、开采年限等,也与矿山投资,投产、达产时间,设备数量,矿山人员和矿石成本等一系列技术经济指标有密切联系,以至最终影响矿山的经济效益[1]。为此,本文以实现矿山利润最大化为目的,借助金融学实物期权理论来分析露天采矿边际品位最优化问题,并建立了经济数学模型,为矿山企业提供决策依据。
1 实物期权的期权定价理论估值模型
西方经济学中用期权定价理论对实物期权进行估值。期权定价理论是对金融期权估值的方法,以布莱克与肖莱斯为代表的布-肖期权定价模型是期权定价理论的重大突破。
t时刻,用 V表示某个投资项目的未来收益的现值,未来收益符合布朗几何运动,则有:

式中:μ——期望收益率;
σ——标准差;
dz——维纳过程增量。
当可用交易证券复制投资项目的现金流时,设交易证券的期望收益率为μ*,令μ<μ*,并设δ=μ*-μ,在这里可以把δ理解为与股票红利相似的投资项目产出现金流。设投资项目基础资产的实物期权的价值为 F,V为项目价值,F为时间 t和项目价值 V的函数,记 r为无风险利率。因此,价值 F为该投资项目拥有的一个实物期权,∂F/∂V为已卖空的项目资产份额,∂F/∂V随 V的变化而调整。由布朗几何运动方程和伊藤引理,可得实物期权的估值模型[2,3]:

2 基于期权定价理论的露天采矿边际品位优化数学模型
2.1 连续变量期权定价数学模型的建立
在边际品位优化研究当中,边际品位是一个变量,而且是连续变化的,针对边际品位变量的连续性,可以从实物期权的内容中找出与之对应的期权类型,即可以引用连续变量期权来分析矿石价格变动情况下的边际品位优化问题。根据连续变量期权的定义,优化时须依据矿石的市场价格来适时调整矿山的生产行为,以使矿山企业利润最大化。
一个工程或者项目在运营的过程中,一般可根据外部或内部环境对项目的某些运营参数进行调整,比如在某个时间点,调整人力、物力和财力等投入以改善经营状况。在某一时间点或者时间段内,这种调整的最优程度取决于那一时间点或者段内产出物的市场价格,达到利润最大化时,要满足边际收益等于边际成本这一必要条件。所以,反过来,当产品的市场价格变化时,要想实现最佳的效益,项目可通过调整其经营参数来实现,调整经营参数后,对项目的估值也需调整[4]。
在市场经济条件下商品价格 K呈随机变动,并且认为在价格变动的某一时刻可对项目的投入进行调整,其调整变量为 v,设 h(v)为其产出的生产函数,c(v)为其相应产生的成本,I(K)为由此带来的利润。因此,使 I(K)最大时的 v即为最优的,即:

根据一维柯布道格拉斯生产函数[5],有:
并可得获得最大利润时,调整变量 v为:

其中,价格 K是变动的,c是不变量,为投入物价格。
将式(5)代入式(4)得产出物函数 h(v):

由此可得最大利润:

记 Φ=(1-θ)(θ/c)θ/(1-θ),γ=1/(1-θ),有 :

考虑到 K是随机变动量,依据式(2),得:

由上式可得:

式中 :Φ=(1-θ)(θ/c)θ/(1-θ);

以上数学模型即为变量呈连续不断变化时的期权定价数学模型。在投入不断调整的时候,用此模型可对项目定价或估值。
2.2 露天采矿边际品位优化数学模型的建立
借助以上的期权定价数学模型对矿山采矿品位进行优化研究。在矿山生产能力一定的时候,边际品位的变动会影响到从爆堆矿岩中装运到选矿厂处理的矿石量的多少,边际品位定得越高,从单位爆堆中获得的矿石量就越少,为了满足选厂对矿石的需求,就必须增加爆堆矿岩量,这种对应关系正好与式(8)所表达的关系是一致的。
记单位爆堆矿岩的成本为 m,所以当边际上增加 1t矿石时,它的边界成本就是m。当矿山生产能力一定并提高边际品位时,矿山所获得的金属产量就增多,增加多少则取决于矿石的品位分布,从前面的分析可知,对于某个矿山,可以用生产函数 h(v)来表示其金属量的产出,这里的 h(v)由矿石品位分布确定,因此,在矿石价格变动情况下,借助式(8)就可以定价或评估采矿边际品位优化调整后的矿山价值。
当边际品位为α时,按照矿山生产能力所需要的爆堆矿岩量为 Qα,设 h(Qα)为金属量生产函数,则有:

式中:Q——选矿生产能力(常数);
ε——回收率(常数);
b——常数。

式(9)即为金属产量和爆堆矿岩量间的函数关系。将式(9)代入式(3)可得矿山利润函数关系式:

将上式对 Qα求导,并令其等于零,有:
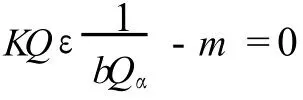
由此式解得 Qα为:

上式即为在矿石价格变动情况下,最优的爆堆矿岩量计算式。因此有最大利润函数式:

根据式(2),可得:

式(11)求解起来很复杂,为了简化计算,在这里利用经济学中的一维柯布道格拉斯生产函数[5]来近似金属量生产函数,即:

为了进一步简化模型,可以不考虑入选成本 c和企业固定费用 f,因为它们与边际品位的调整没有关系。在这里只需考虑爆堆矿岩成本 m,所以,矿山利润可表达为:

解得最优的 Qα为:

对应的金属产出量为:

由式(7)可得:

令 Φ=(1-lθ)(lθ/m)θ/(1-θ)

根据式(8),可构建出露天矿山价值的经济数学模型为:

式中:Φ′=(1-lθ)(lθ/m)θ/(1-θ)

h(Qα)吨金属卖出后的收益为:

令 V(K)=V(K) ′,即
Φ′Kγ/δ′=QαεK,解得 :

式(14)即为最优边际品位的计算式,矿山以此边际品位为根据来进行采矿活动,能够使矿山利润最大化。
3 案例分析
某金属露天矿单位爆堆矿岩成本m=10元/t,单位矿石入选成本 c=10元 /t,矿山固定费用 f=1950万元,选场处理矿石能力 Q=150万 t/a,选矿回收率ε=95%,精矿价格 K=6000元 /t,边际品位α=1.2%,无风险利率 r=0.8,标准差σ=0.15,rδ=0,b=300。
假设该金属露天矿矿体品位分布函数为负指数函数,那么由式(9)知,该矿金属量生产函数为:


Qα和 h(Qα)存在一一对应关系,对 Qα取不同的值,就能得出不同 h(Qα)(见表1)。

表1 爆堆矿岩量与金属产量对应关系
对金属产量进行线性拟合,得该矿生产函数为:

所以,γ=1.5,δ′=0.0716,Φ′Kδ=5102(万元)于是:
V(K)K=6000=71229(万元)
扣除选矿费用和固定费用后,该矿项目价值为:
V(K)=71229-(1950+10×150)×1/0.08=28034(万元)
按式(13)计算,其年利润为 1797万元,按式(12)计算,并以 0.08进行折现后,其年利润为 2243万元。所以,运用本文所建模型来决策矿山边际品位,能够使矿山多盈利约 446万元。
4 结 论
本文运用实物期权理论建立了露天采矿边际品位最优化的数学模型,这一模型充分地体现了采矿边际品位的经济意义,实现了矿山企业追求利润最大化目标。在市场经济条件下,该模型为矿山的采矿品位决策提供了一个新的有效的途径。
[1] 海跃华,何 琦.七宝山金矿合理边际品位研究[J].矿冶工程,2009,3:8~12.
[2] 刘玉平.金融学[M].上海:复旦大学出版社,2007.
[3] 廖 奕.金融学[M].北京:机械工业出版社,2008.
[4] 张顺堂.金属矿山经营参数动态优化综合模型研究[J].矿业研究与开发,2005,25(3):1~2.
[5] 臧良运.西方经济学[M].北京:科学出版社,2008.
2010-05-18)
郝全明(1957-),男,内蒙古包头人,教授,硕士生导师,主要从事矿业系统工程、采矿工艺与技术、矿业技术经济等研究。

