中国货币政策的福利损失及中介目标的选择*——基于新凯恩斯DSGE模型的分析

奚君羊,贺云松

(上海财经大学 金融学院,上海 200433)

一、引 言

近年来,中国以货币供应量为中介目标的货币政策是否有效的问题已成为学术界关注的热点。夏斌和廖强(2001)从货币传导机制角度分析了货币供应量目标无效的深层原因,并指出货币供应量中介目标客观上已不合时宜,应尽快废止,同时还提出了通货膨胀目标制。奚君羊和刘卫江(2002)通过模型分析支持了上述观点。陈利平(2006)则在一个引入时滞和货币政策传导扰动的货币政策模型中分析了货币存量中介目标制下中国货币政策的低效率问题。中国学术界对货币政策的讨论主要集中在对货币政策规则的研究上。刘斌(2003)根据中国的实际数据估计出混合模型,并在此基础上计算和比较了三种货币政策决策方式对社会福利的影响。卞志村和管征(2005)则采用一个简单的前瞻性模型分析了货币当局确定最优货币政策规则的过程。谢平和罗雄(2002)运用泰勒规则对中国的货币政策做了实证研究。

上述文献在很大程度上丰富了中国有关货币政策的研究成果,但在分析中主要运用广义矩法(generalized method of moments,GMM)等计量方法对模型进行估计,由此容易产生以下问题:首先,GMM估计的参数必须以大样本为基础,而中国目前可获得的有关数据则非常有限;其次,GMM估计中工具变量的选取要求其具有与方程残差不相关以及与解释变量相关两个性质,而现实中恰当的工具变量却难以找到。上述情况使得GMM估计结果的可靠性难以得到保证。为此,本文运用动态随机一般均衡模型(dynamic stochastic general equilibrium,DSGE)以分析货币政策规则。

DSGE模型是基于实际经济周期(Real Business Cycle,RBC)理论分析宏观经济问题的主要工具。DSGE模型的优势在于它不受制于“卢卡斯批判”(Lucas critique),①因为在DSGE模型中有关宏观经济变量的行为方程都被消费者和厂商的跨期一阶均衡条件所代替,有关预期如何形成的事后假设也被理性预期所替代。此外,DSGE模型强调使用校准、模拟等方法来对模型进行数量分析。最后,运用DSGE模型还能清楚地分析货币政策的传导机制。

近十多年来,国际学术界在对货币政策、通货膨胀以及经济周期之间关系的研究方面逐步形成了一种新的分析框架,即所谓的新凯恩斯模型(New Keynesian Model)。新凯恩斯模型有着类似于RBC模型的核心结构,那就是把DSGE模型作为主要的分析工具。新凯恩斯模型在RBC模型的基础上加入了一些凯恩斯模型的特征,如垄断竞争的市场结构、名义刚性等,这也使得一些学者把这一新的分析框架称为新新古典综合论(New Neoclassical Synthesis)。

基于上述考虑,本文将运用新凯恩斯框架下的DSGE模型来分析货币政策,并从福利的角度来评价不同的货币政策的效果。其基本思路为:在一个统一的模型框架内分析中国现行的货币政策以及不同类型的利率规则的福利损失的大小,通过校准和数值试验来对各种利率规则的表现做出比较分析,进而为中国货币政策的改进提出相关建议。

二、DSGE模型的构建

现代新凯恩斯框架通常使用没有货币的模型来研究货币问题,因为在利率规则下货币是内生的,货币供应量唯一的作用在于使得货币市场出清。然而本文不仅要研究利率规则,而且要考察货币供应量,因此不可避免地要涉及货币,为此我们使用Gali(2008)的方法,即在必要的时候对模型补充一个事后的(ad-hoc)对数线性货币需求函数:

其中,mt,pt,yt和it分别表示货币、价格、产出和名义利率,b为产出的系数,η是货币需求对利率的半弹性。②模型的其他方面则是一个标准的新凯恩斯模型,即在RBC模型的基础上引入垄断竞争和粘性价格两种特征。下面我们将建立相关模型。③

(一)家庭行为

假设一个永久生存的代表性家庭最大化目标函数为:

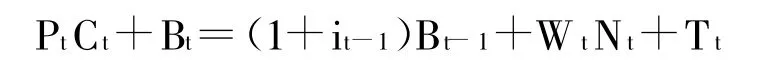
其中,Bt表示家庭在第t期购买的名义债券数量,it-1表示在第t-1期的名义利率,Wt表示名义工资,Tt表示总量税以及拥有工厂所有权得到的分红等。最后假设家庭满足非庞氏博弈(no-Ponzi-game)条件,④家庭在约束条件下令效用函数(等式2)最大化,其一阶条件经对数线性化后为:

其中πt+1=pt+1-pt为第t期到第t+1期之间的通货膨胀率,ρ=-log(β)。

(二)厂商行为

假设每种商品i∈[0,1]由一个垄断竞争厂商生产,每个厂商i使用同样的技术,其生产函数为下面的规模报酬不变的线性形式:Yt(i)=AtNt(i),其中,At表示外生的技术冲击,Nt(i)为厂商i雇用的劳动。假设技术冲击的对数服从AR(1)过程:at=ρaat-1+,其中ρa∈[0,1],而为白噪声。所有的厂商把总价格水平Pt和总消费指数Ct当作是给定的,假定价格存在粘性,根据Calvo(1983)和Yun(1996),每期有θ∈[0,1]比例的随机抽取的厂商不能调整其产品的价格,其余的1-θ厂商可以对其产品重新定价。厂商问题的最终解为:

其中λ=(1-θ)(1-βθ)/θ,m^ct+k=mct+k-mc表示实际边际成本与其在稳定状态时的值之差,πt=pt-pt-1为第t-1期到第t期的通货膨胀率。

(三)市场均衡

首先,产品市场出清要求对所有的商品i∈[0,1]满足Yt(i)=Ct(i),定义总产出水平为则有Yt=Ct。其次,劳动力市场出清要求yt=at+nt。然后根据家庭和厂商的均衡条件以及市场出清条件经推导就可以得到新凯恩斯菲利普斯曲线。在产出缺口的路径已定时,通货膨胀率(πt)便由下式决定:

动态IS曲线则表现为:

(四)货币政策

为了把货币政策引入模型,我们把货币需求函数(等式1)改写为lt=b(+)-η it,其中lt=mt-pt为实际货币余额,于是有lt-lt-1=Δmt-πt,其中Δmt=mt-mt-1为货币供应量增长率,假设其服从 AR(1)过程:Δmt=ρmΔ mt-1+,其中ρm ∈[0,1),而为白噪声 。

假设货币当局根据下面的T aylor(1993)类型的简单规则来设定短期的名义利率:

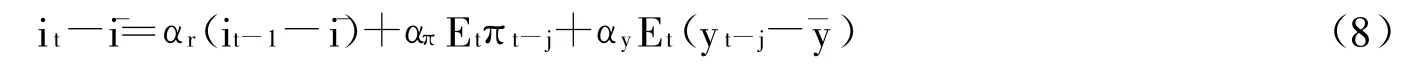
其中,απ、αr和 αy都是系数,i¯和 ¯y分别为稳定状态时的利率及产出,j=0,1,-1。当j=0时,利率规则将根据当期的通货膨胀率以及产出水平来设定名义利率,在本文中为区分各种利率规则我们称其为泰勒规则;当j=-1时,利率规则是前瞻型的,即货币当局根据对通货膨胀率以及产出水平的下一期的预期值来设定当期的名义利率;当j=1时,利率规则是后顾型的,即货币当局根据通货膨胀率以及产出水平的上一期的值来设定当期的名义利率。在所有三种类型的利率规则中,当αr不为0时货币当局根据上期的名义利率值对利率做出逐步调整,即存在利率平滑(smoothing)现象。

三、模型的校准及福利测算

(一)福利损失

本文以福利为标准来评价不同的货币政策,并以代表性家庭的终身效用来衡量福利。假设政府可以通过总量税融资的就业补贴以消除垄断竞争所引起的市场扭曲,那么模型中唯一的市场扭曲就来自价格粘性。根据这样的假设,稳定状态时的资源配置是最优的。我们将货币政策的福利损失定义为稳定状态时消费量下降的百分比,则实施某一货币政策α时,代表性家庭的福利为而稳定状态时的福利为用λα表示采用政策α时的福利损失,则有

根据Woodford(2003),每期的平均福利损失为产出缺口和通货膨胀率的方差的线性组合:

其中λ=(1-θ)(1-βθ)/θ。从等式(9)可以看出,最优的货币政策要求产出缺口和通货膨胀率都为0,福利损失中产出缺口方差的权重与风险厌恶系数σ、弗里施(Frisch)劳动供应弹性的倒数φ成正比,通货膨胀率方差的权重与产品需求替代弹性ε以及价格粘性程度θ成正比。对模型的结构参数进行校准之后,我们就可以计算中国的货币政策以及不同利率规则下的通货膨胀以及产出缺口的方差和相应的福利损失。下面我们根据中国经济的实际数据以及有关粘性价格模型中的常用参数值对模型的参数进行校准。

(二)参数校准

我们所用的数据为中国1992年第一季度到2008年第四季度的GDP、CPI和城镇就业人数,以及1997年第三季度到2008年第四季度的货币供应量(M2)和3月期的国库券利率。之所以选择这一特定时间段是因为从1997年第三季度才开始有3月期国库券利率的数据,而本文的模型是季度模型,选用3月期国库券利率比较合适。本文的数据来自中经网数据库和万得(Wind)数据库。通过使用普通最小二乘法(OLS)得到参数b的值为1.17,参数η的值为2.58,货币供应增长率的一阶自回归系数ρm为0.92,货币供应冲击的标准差σm为0.0151。为确定技术冲击的一阶自回归过程,我们使用劳动生产率(由于假设生产函数是线性的,本文中劳动生产率和索罗剩余是一致的)来代替技术冲击,⑤并对劳动生产率取对数后再进行Band-Pass滤波以消除趋势,其中Band-Pass滤波的下限和上限分别取6和32,这样经滤波后时间序列只保留了周期为1.5年到8年的部分,再使用OLS就可以得到技术冲击的一阶自回归系数ρα为0.83,标准差σα为0.0149。

对于消费者的主观贴现因子β,我们取值为0.989,这在有关RBC文献中是常用值,没有什么争议。对于风险厌恶系数σ,根据黄赜琳(2005)的研究将其值设定为0.7。参数φ为弗里施(Frisch)劳动供应弹性的倒数,根据King和Rebelo(2000)将其值设定为1。对于产品需求的价格弹性ε,根据陈昆亭和龚六堂(2006)的研究将其值设定为10,这也就意味着在稳定状态时厂商的价格加成为11.11%。至于反映粘性价格程度的参数θ,Christiano和Eichenbaum(2005)的估计为0.8,陈昆亭和龚六堂(2006)所使用的值为0.6,本文将其值设定2/3,这意味着厂商的平均调价周期为三个季度。这样就完成了对所有结构参数的设定(见表1)。

表1 模型的结构参数

四、模拟结果

在确定模型的结构参数后我们使用Klein(2000)的广义舒尔(Schur)分解方法求得模型在稳定状态附近的线性近似政策函数(policy function),然后对模型进行模拟就可以得到产出缺口和通货膨胀率的方差以及对应的福利损失(本文中所有的结果都是通过MAT LAB编程计算得到的)。为分析利率规则(等式8)中不同参数值对福利的影响,我们将απ、αr和αy的取值范围定在0到3之间。表2给出了三种利率规则下απ、αr和αy取一些特定值时产出缺口和通货膨胀率的标准差σ和σπ以及相应的福利损失大小,这些统计量的单位均为百分数。

表2的前两列反映了利率系数和产出系数都为0时不同通货膨胀系数对福利损失的影响。当通货膨胀系数分别取1.5和3.0时,在泰勒规则下福利损失从0.031%下降到了0.003%,在前瞻型规则下福利损失从0.071%下降到了0.006%,在后顾型规则下福利损失从0.068%下降到了0.027%;表2的第三列和第四列给出了当通货膨胀系数为1.5以及利率系数为0时产出系数分别为0.1和0.5时的福利损失,在三种规则下福利损失都随着产出系数的增加而大幅上升,在泰勒、前瞻型、后顾型规则下福利损失分别上升了大约4倍、3倍和3倍;表2的最后三列给出了当通货膨胀系数为1.5以及产出系数为0时利率系数取不同值时的福利损失,当利率系数分别取0.1、1.0和3.0时,在泰勒规则下福利损失从0.023%下降到0.009%,在前瞻型规则下福利损失则是从 0.051%上升到 0.084%,在后顾型规则下福利损失从0.066%下降到0.019%。然而这种下降和上升并不是单调的,这一点从图1的第三个小图可以清楚地看到。

图1给出的是取值范围在0到3之间的不同απ、αr和αy值在泰勒、前瞻型和后顾型三种利率规则下的福利损失。第一个小图描绘的是利率系数和产出系数都为0而通货膨胀系数取值从1.1到3.0时的福利损失。第二个小图描绘的是利率系数为0、通货膨胀系数为1.5时产出系数取值从0.1到1.0时的福利损失。这里的产出系数并没有取值到3.0,这是因为数值试验表明当产出系数大于1.33时模型的均衡解并不是唯一的。第三个小图描绘的是产出系数为0、通货膨胀系数为1.5时利率系数取值从0.1到3.0时的福利损失。

表2 特定参数设置下各种利率规则的福利损失

图1 不同参数设置下各种利率规则的福利损失

五、结论及政策建议

根据上述分析并结合表2和图1我们得出以下主要结论和政策含义:

结论一:在其他两个参数不变的情况下名义利率对通货膨胀的反应系数απ越大则福利损失越小。从图1的第一个小图可以明显地看到福利损失随απ单调递减,当απ为3时泰勒规则和前瞻型规则下的福利损失都非常接近最优货币政策,分别为0.003%和0.006%,后顾型规则下的福利损失也只有0.027%。

本文的模型假定价格在短期内存在粘性,而不同的产品其价格粘度又不完全一致,这样,在受到技术冲击时不同产品的价格上升幅度(价格加成)就有差异,这种价格的结构性变化将会导致不同产品的消费和产量的变动幅度出现差异,一些产品可能出现供过于求,另一些产品却存在供不应求。这种结构性的供求失衡意味着福利的损失。为了避免这种损失,就需要使所有的厂商都满足于现存的价格水平而没有调价的意愿。换言之,如果货币当局能通过利率政策抑制通货膨胀,则价格的结构性变动幅度就有望下降,结构性的供求失衡相应缓解,福利的损失也就减少(见等式9)。因此,名义利率对通货膨胀反应系数越大,通货膨胀的方差就越小,福利损失也越小。这就为货币当局运用利率政策稳定价格水平提供了充分的依据。中国货币当局为追求较高的经济增长速度往往在通货膨胀明显偏高的时期依然维持较低的利率水平,以致实际利率常常为负值。这种做法可能导致巨额的福利损失,值得反思。

结论二:在其他两个参数不变的情况下名义利率对产出的反应系数αy越大则福利损失越大。从图1的第二个小图可以明显地看到福利损失随αy单调递增,当αy为1时在泰勒、前瞻型和后顾型规则下的福利损失分别为0.805%、1.07%和1.647%。

货币政策的目标并非产出水平,而是实现均衡的产出,即产出缺口为0,既要避免产出过剩,也要防止供不应求,其理论含义是使产出水平与产出的自然率水平保持一对一的变动。如果产出的下降是宏观经济的供过于求造成的,是经济实现均衡的要求,而货币当局却一味以调低利率的货币政策追求产出增长,结果反而使产能过剩的现象持续存在,进而扩大福利损失。因此,名义利率对产出的反应系数αy越大,则福利损失也越大。换言之,如果我们试图运用利率政策来影响产出,其结果可能适得其反。

结论三:利率平滑对福利的影响不大。从图1的第三个小图可以清楚地看到,在泰勒规则和后顾型规则下福利损失基本上是一条水平线,在前瞻型规则下福利损失随利率系数αr的上升先降后升,但是福利损失的大小变化并不大,其取值范围大概在0.04%到0.08%之间。可见,利率平滑对福利的影响较小,在前瞻型利率规则下利率平滑还有可能导致福利损失的增加,因此,货币当局的利率政策应该直接针对通货膨胀,而不应该追求利率本身的稳定。

结论四:在一定的参数范围内三种利率规则的福利损失较为接近。从图1的第一个小图可以看出,当通货膨胀系数取值大于1.6时三种规则下的福利损失相差不大。从利率政策实施的便利性看,前瞻型利率规则需要对产出和通货膨胀的未来值做出精确预测,这一点在实际操作过程中是比较困难的。就泰勒规则而言,由于统计数据存在滞后性,实际操作起来也不容易。因此,我们建议采取后顾型利率规则,因为该规则更加可行,且产生的福利效应与其他利率规则并无很大差异。

我们对中国货币供应量政策的福利损失也进行了分析,模型的模拟结果为5.0735%,相应的通货膨胀和产出缺口的标准差分别为4.11%和3.39%,这一结果远远大于在利率规则下的数值。即使是在没有货币供应冲击的固定货币供应的规则下(Δmt=0)福利损失也高达0.1888%,对应的通货膨胀和产出缺口的标准差分别为0.7427%和1.6992%,这也比在合理设置参数值的利率规则下的福利损失大得多。因此,即使在货币当局能精确控制货币供应量的情形下货币供应规则的福利损失相对利率规则而言也是比较大的。这种现象表明,中国的货币政策的中介目标应该逐步由货币供应量转向利率水平,更多地运用利率政策来稳定价格水平。

注释:

①卢卡斯认为,人们的预期对宏观经济变量有着重要的影响,因此,如果计量模型中缺乏包含了政策预期的微观基础,其预测效果就会失真。

②本文的数学等式中所有的大写字母表示各变量的水平值,而小写字母则表示对应的变量的自然对数值。

③限于篇幅,本文没有给出模型的详细推导过程,感兴趣的读者可以通过电子邮件(junyang@shufe.edu.cn)向作者索取。

④Ponzi又译蓬齐。

⑤按照索罗的观点,除了劳动和资本以外,其他(剩余)因素,尤其是技术,即劳动生产率对产出也有重要贡献。

[1]夏斌,廖强.货币供应量已不宜作为当前中国货币政策中介目标[J].经济研究,2001,(8):14-16.

[2]奚君羊,刘卫江.通货膨胀目标制的理论思考[J].财经研究,2002,(4):3-8.

[3]陈利平.货币存量中介目标制下中国货币政策低效率的理论分析[J].金融研究,2006,(1):40-50.

[4]刘斌.最优货币政策规则的选择及在中国的应用[J].经济研究,2003,(9):3-13.

[5]谢平,罗雄.泰勒规则及其在中国货币政策中的检验[J].经济研究,2002,(3):3-12.

[6]陈昆亭,龚六堂.粘滞性价格模型以及对中国经济的数值模拟[J].数量经济技术经济研究,2006,(8):601-711.

[7]黄赜琳.中国经济周期特征与财政政策效应[J].经济研究,2005,(6):27-39.

[8]卞志村,管征.最优货币政策规则的前瞻性视角分析[J].金融研究,2005,(9):31-38.

[9]Calvo,Guillermo.Staggered prices in a utility maximizing framework[J].Journal of Monetary Economics,1983,(12):383-398.

[10]Jordi Gali.Monetary policy,inflation,and the business cycle[M].Princeton University Press,2008.

[11]Klein P.Using the generalized schur form to solve a multivariate linear rational expertations model[J].Journal of Economic Dynamic and Control,2000,(24):405-423.

[12]Taylor John B.Discretion versus policy rules in practice[J].Carnegie Rochester Conference Series on Public Policy,1993,(39):195-214.

[13]Woodford Michael.Interest and prices:Foundations of a theory of monetary policy[M].Princeton University Press,2003.

[14]Yun Tack.Nominal price rigidity,money supply endogeneity,and business cycles[J].Journal of M onetary Economics,1996,(37):345-370.