抗差估计的选权迭代法分析与比较
陈西强,黄张裕
(河海大学 测绘科学与工程系,江苏 南京 210098)
抗差估计的选权迭代法分析与比较
陈西强,黄张裕
(河海大学 测绘科学与工程系,江苏 南京 210098)
在抗差稳健估计中,选权迭代法应用最广,较易理解,M估计法计算简单。基于M估计的基本理论,深入分析Huber、Hampel、IGG 3种常用的选权迭代法,并利用水准网数据,分析这3种常用选权迭代法的适用范围和相应的抗差效果,表明IGG法比其他两种的抗粗差效果要好,且易实现。
抗差稳健估计;选权迭代法;Huber法;Hampel法;IGG法
在抗差稳健估计中,最常用的为M估计法,其估计方法有许多种,其中选权迭代法应用最广,较易理解,计算简单。对于选权迭代法,理论研究相对比较多,但对其中的参数选取,在理论上有所研究,实际应用研究上存在不够深入和不足的问题[1-2]。本文在分析M稳健估计基本理论的基础上,讨论了3种常用的选权迭代法。选用水准网实例,深入分析3种选权迭代法的初始权选取和条件参数选取,并从纵横两个方面来进行比较、分析这3种常用选权迭代法的适用范围和相应抗差效果,表明IGG法比其他两种方法的抗粗差效果要好,且易实现。
1 M稳健估计
设有参数向量X是未知的非随机量,为了估计未知向量值,进行n次观测得到向量L的观测值l,由极大似然估计有[3]
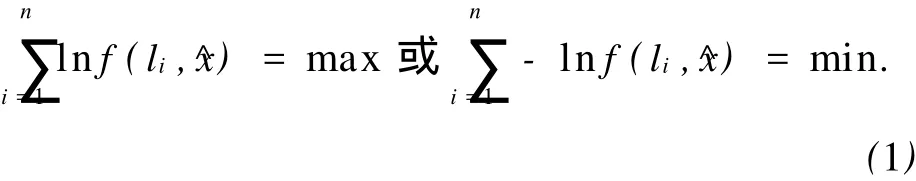
式中:f是随机量L的密度函数。
Huber提出用ρ(li,x)代替函数-lnf(li,^x),使其定义广义化,于是有

式中:φ(li,^x)=∂ρ(li,x)/∂x。
由式(2)对参数x进行估计,就是广义极大似然估计,简称M估计。测量平差中,观测量L的残差为V,M估计的函数ρ可取为ρ(vi),即M估计的准则为

通常残差V为未知数的函数,将式(2)对未知数x求导,取极值点,则有
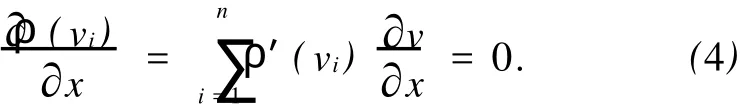
考虑到误差方程vi=ai^x-li,ai为A的第i行向量,则有

令权函数pi(vi)=ρ′(vi)/vi,即得

用矩阵表示为

式(7)类似最小二乘估计的法方程形式,用权函数矩阵P(V)=diag(p1(vi),p2(vi),…,pn(vi))代替观测权阵P。为此,可将稳健估计的选权迭代法归结为如下模型:
误差方程与权函数为

估计准则为
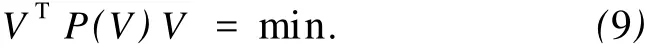
将平差模型转换为最小二乘估计的模型,采用类似最小二乘估计。只是权函数P(V)是残差的函数,计算前V未知,只能通过给其赋予一定的初值,采用迭代法估计参数^x。具体计算过程如下:
1)列误差方程,令各观测权函数初值均为1,即令p1(vi)=p2(vi)=…=pn(vi)=1。
2)解算法方程,得出^x和V的第1次估值^x(1)=(ATA)-1ATl,V(1)=A^x(1)-l。
3)由V(1)确定各观测权函数pi(vi),再解算法方程,通过迭代计算,直到前后两次解的差值符合要求为止。
4)最后结果为
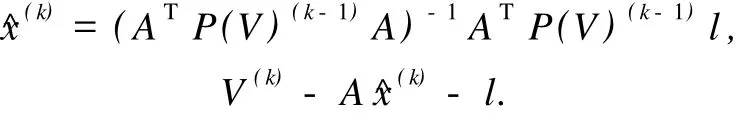
随着函数ρ的选取不同,可以构成权函数的多种不同的形式,通常权函数是一个在平差过程中随改正数变化的量,经过多次迭代,使含有粗差的奇异观测的权函数为0(或者接近于0),而相应的残差值在很大程度上反映了其粗差值[4-5]。
2 几种常用的选权迭代法
2.1 Huber法
Huber法的极值估计准则是假设观测值在不利分布情况下求最优估计[6]。取M估计的函数
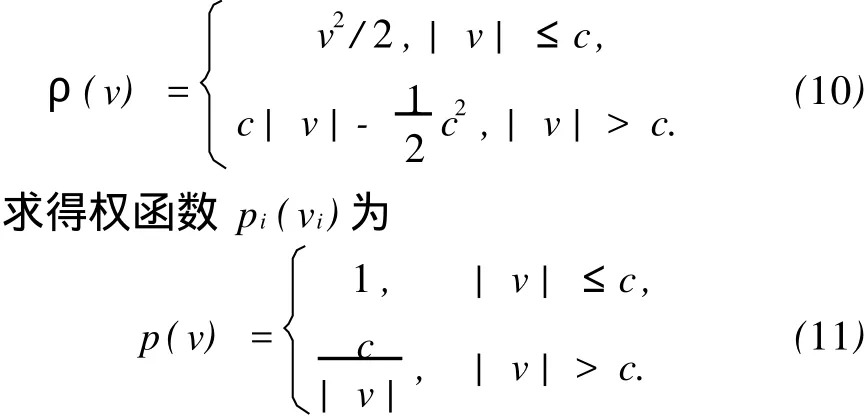
由Huber权函数可以看出,Huber估计的权函数是单调的,它在c处的斜率有突然变化。当所有改正数均在-c和c之间时,Huber估计就是经典最小二乘法估计[7]。而当部分改正数大于c时,其p(v)与改正数成反比,v愈大,对应的p(v)愈小,与此相应该观测值对参数估计的影响也愈小。
2.2 Hampel法
对于Hampel法,取M估计的函数为3段截尾函数

求得权函数pi(vi)为
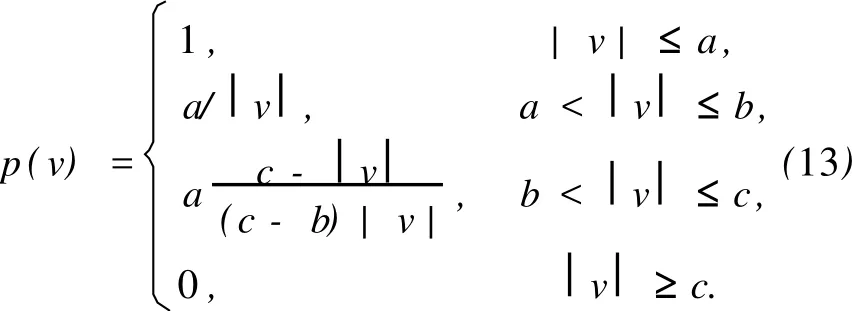
式中:a、b、c为3个系数,可适当选取,它们均为标准差的倍数。
2.3 IGG法(周文江法)
IGG法是由中国科学院测量与地球物理研究所周文江教授最初提出的,取M估计的函数[8]
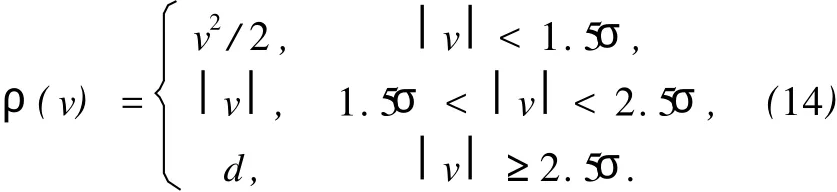
求得权函数pi(vi)为

IGG法属于有淘汰区的M估计,权因子之间变化比较平缓,k值一般取一个很小的数。
3 实例分析
水准路线如图1所示。

图1 水准路线
如表1所示水准网,A、B两点的已知高程分别为HA=5.000 m,HB=6.000 m,观测了7条水准线路,表中带*号的表示有粗差的观测值,对h2赋以粗差0.050 m,h6赋以粗差-0.030 m。根据水准路线观测数据,按最小二乘原理,在不含有粗差和含有粗差的条件下分别解算,如表2所示。

表1 水准网观测数据

表2 基于最小二乘解算结果
3.1 3种方法分析
对于 Huber法分析c选取对估计结果影响。在迭代过程中,σ值随每次迭代后算出的观测改正值来确定。在本次数据分析中,c分别取 0.4σ、0.8σ、σ、1.2σ、1.6σ、2.0σ、2.5σ,试验数据结果如表3所示。

表3 c选取对估计结果的影响
从表3的数据可以知道,随着c取值的增大,总体上中误差越来越大,迭代次数越来越多,到达一定的时候,迭代效果失效。而且当c为一倍中误差的时候,Vh2和Vh6的改正值是最能反映出含有粗差的数据,但总体效果不是很理想。
对于Hampel法分析a、b、c的取值对估计结果影响。a、b、c3个系数分别取4组值进行比较分析,即取a=0.9σ,b=1.8σ,c=2.7σ;a=σ,b=2σ,c=3σ; a=1.1σ,b=2.2σ,c=3.3σ和a=1.2σ,b=2.4σ,c= 3.6σ,试验数据结果如表4所示。

表4 a、b、c取值对估计结果的影响
从表4数据分析可知,在a、b、c三者的相互间隔增大的同时,方案1、2、3的估计结果没有大的变化,只是中误差和迭代次数都有所增大。当三者之间的间隔超出了一定的范围时,必将导致估计失效。试验分析得出间隔应在0.9~1.1之间,而且当间隔太小时,会导致求解过程中的权阵单极化。
对于IGG法分析k取值对估计效果影响。分别取k为0.001、0.000 1、0.000 01,试验所得数据如表5所示。
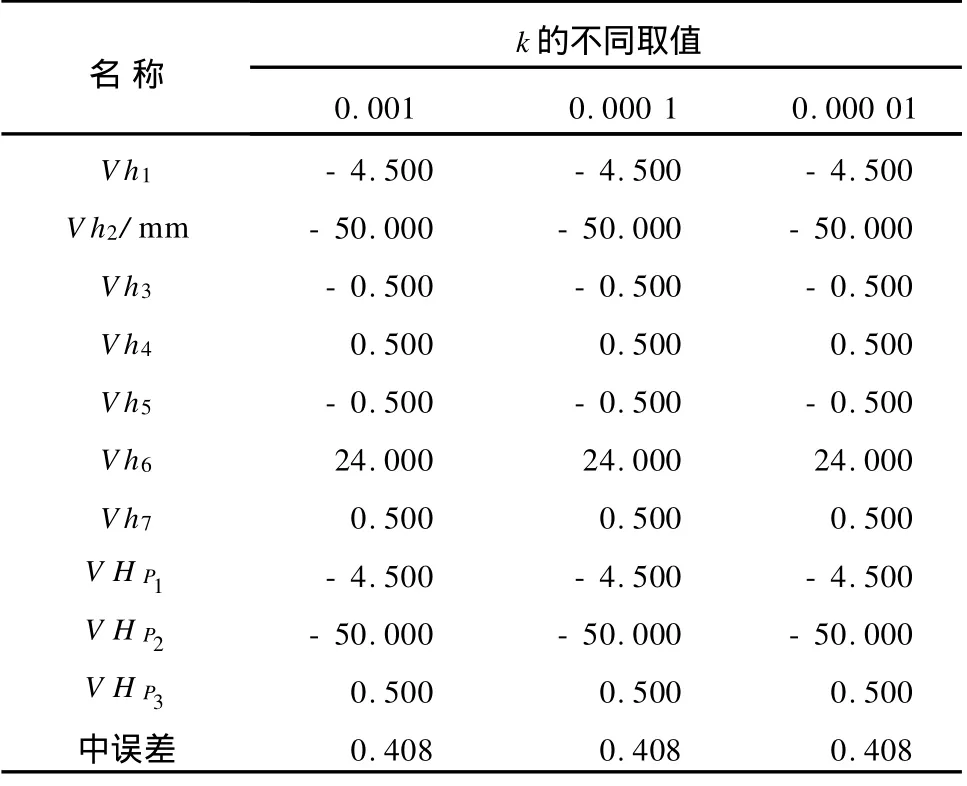
表5 k取值对估计效果的影响 mm
从表5的数据分析可知,只要k值在一定的范围之内,即对估计的效果没有影响。权函数中的条件是随着每次迭代得到的中误差,在整个迭代过程中是变化的,而且越来越低,随着满足迭代条件而终止。
另外,对于3种选权迭代方法,分别分析初始权选取对估计结果的影响。在试验分析中分别采用了初始权都为1和初始权按距离定权的2种方案进行数据分析,3种迭代方法计算结果完全相同,数据结果如表6所示。

表6 初始权选取对估计结果的影响 mm
从表6的数据分析可以看出,初始权的选取对3种方法的估计结果都没有影响。
3.2 3种方法比较分析
现对Huber、Hampel、IGG方法作横向比较,由这3种方法分别对这个已知含有粗差的水准网观测数据进行平差处理,得到的结果如表7所示。

表7 不同选权迭代法比较
从表7的数据分析可知,在粗差较大的情况下,在迭代次数和最后的精度及计算结果综合因素来看,IGG法比 Hampel法和Huber法效果要好。在抗粗差及剔除粗差方面,IGG和 Hampel都能很好地剔除由于h2带来的粗差0.050 m和h6已赋的粗差-0.030 m,而Huber法相对来说要差点,而且在Huber法中的c值的选取好坏直接影响到抗粗差的能力。
4 结 论
1)稳健估计中的选权迭代法在初始化权方面都是相同的,即估计结果不受初始权的取值影响,且在选权迭代过程中,对于选权的标准或条件系数都是随着每次迭代完后重新计算的中误差相关,说明3种选权迭代的条件系数是动态的。
2)对于 Huber法,随着c取值的增大,总体上中误差越来越大,迭代次数越来越多,到达一定的时候,迭代失效,而且当c为1倍中误差时,Vh2和Vh6的改正值是最能反映出含有粗差的数据,但效果不是很理想,因此,在含粗差较大时,建议 Huber法中c的取值范围为中误差的0.8~1.2之间。对于Hampel法,a、b、c三者的取值在一定范围内相互间隔增大时,估计结果没有大的变化,只是中误差和迭代次数都有所增大,当三者之间的间隔超出了一定的范围,将导致估计失效,试验结果表明间隔应在0.9~1.1之间,而且当间隔太小时,会导致求解过程中的权阵单极化。在IGG法分析中,k的取值足够小就能满足要求,如本文试验k值取0.001~0.000 01。
3)在这3种稳健估计的选权迭代法中,IGG法比其他两种的抗粗差效果要好,且易实现;在不清楚数据分布的情况下,建议采用IGG法。
[1]陶本藻.稳健估计的应用问题[J].地矿测绘,2000(1): 1-3.
[2]杨元喜.参数M估计及验后精度综述[J].测绘通报, 1991(6):6-10.
[3]刘大杰 ,陶本藻.实用测量数据处理方法[M].北京:测绘出版社,2000:52-58.
[4]吴富梅.多种权函数固定临界值与可变临界值抗差估计的比较[J].测绘工程,2006,15(3):19-22.
[5]李浩军,唐诗华,黄杰.抗差估计中几种选权迭代法常数选取的探讨[J].测绘科学,2006,31(6):70-72.
[6]周江文.经典误差理论与抗差估计[A].抗差估计论文集[C].北京:测绘出版社,1992:1-6.
[7]姚宜斌.基于等价分析法的稳健估计权函数设计[J].测绘工程,2001,10(2):29-31.
[8]杨元喜,宋力杰,徐天河.大地测量相关观测抗差估计理论[J].测绘学报,2002,31(2):95-99.
Analysisand comparison of the selecting weight iteration method in resistance robust estimation
CHEN Xi-qiang,HUANG Zhang-yu
(Department of Survey Science and Engineering,Hohai University,Nanjing 210098,China)
In the robust estimation,selecting weight iteration method is the most w idely understood,more easily and simp le calculation of M estimation.Based on the basic theory of M estimation method,this paper deep ly analyzes three common selecting w eight iteration methodsw hich are Huber、Hampel、IGGmethods,and analyzes the app licable scope and co rresponding poo r effect on the three commonly selecting w eight iteration methods by using the data of the netwo rk level.It show s that the exco rresponding poo r effect of the IGG is better than other two methods,and easy to achieve results.
resistance robust estimation;selecting weight iteration method;Hubermethod;Hampelmethod;IGGmethod.
P207
A
1006-7949(2010)04-0008-04
2009-09-03
陈西强(1986-),男,硕士研究生.
[责任编辑:刘文霞]

