液体食品非稳态导热的研究

吴大伟，吴 迪，倪婷婷

（黑龙江八一农垦大学食品学院，黑龙江大庆163319）

液体食品非稳态导热的研究

吴大伟，吴 迪，倪婷婷

（黑龙江八一农垦大学食品学院，黑龙江大庆163319）

利用非稳态导热的理论，建立数学方程。采用常见的液体食品纯净水、牛奶、橙汁为实验材料，并分别采用圆柱体和长方体容器盛装、封闭，分别用水浴温度50、60、70℃进行加热。通过实验测得的温度、时间数据，确定数学方程中的常数。从而获得圆柱体和长方体在非稳态导热的条件下，中心温度随时间变化的方程。

液态食品，非稳态导热，数学方程

非稳态导热是指温度场随时间变化的导热过程。在食品生产中，水浴杀菌或加热是比较常用的单元操作，但是由于非稳态导热，食品的中心温度总是在不断的变化，如果加热时间过短会造成不能完全杀灭细菌，如果加热时间过长会造成营养物质的损失，并且增加了能耗和操作费用。此外，包装材料规格的不同也会影响非稳态导热的效果。1979年苏联学者S.V Patankar提出了直接求解非稳态导热的基本思想，并对一维问题进行了数值求解［1］。在国内，这方面的研究比较少，主要研究者有杨能彪、孙昆峰和吴建波以及乔春珍等［2-5］。包括上述研究在内的现有成果，在计算非稳态导热的问题时通常要用准数方程和算图，计算过程较繁琐。本研究利用非稳态导热的理论建立数学方程，并通过实验获得被加热物料为圆柱体和长方体时，在非稳态导热的条件下，中心温度随时间变化的方程，从而使这类问题的计算较为简捷。

1 材料与方法

1.1 材料与仪器

纯净水、橙汁 康师傅控股有限公司；牛奶 蒙牛乳业集团。

HH-8数显恒温水浴锅 江苏亿通电子有限公司；WTZ-280温度计 常州市瑞明仪表厂；铁架台、烧杯、层析缸、PS-810秒表 深圳追日电子科技有限公司；IP-67游标卡尺 上海广陆测控技术开发有限公司。

1.2 实验方法

1.2.1 实验原理 一个物体侵入温度为T∞的恒温流体浴之中，该物体初始温度为T0，这时热交换物体内各点温度随时间不断变化，亦即物体内的热导是非稳态导热，热换结果使物体内温度逐渐趋向T∞，直到达到平衡为止。

如果忽略内阻［6］，则：

对于大多数物体的内阻都不能忽略，在此引入校正系数ξ，则上述方程变为：

如果被加热的物体为圆柱体，并且圆柱体的半径为r，圆柱体的长度为L，则：

表1 纯净水在水浴杀菌过程中非稳态导热实验数据及计算

表2 方差分析表

如果被加热物体为液体圆柱体（通过圆筒壁与加热介质隔开），则上述方程变为：

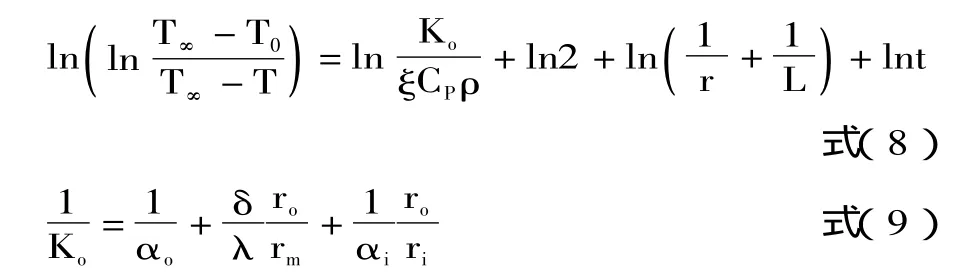
其中：Ko，以外表面为基准的总传热系数；αo，圆筒壁外表面的对流传热系数；αi，圆筒壁内表面的对流传热系数；δ，圆筒壁厚度；λ，圆筒壁的热导率；ro，圆筒壁的外半径；ri，圆筒壁的内半径；rm，圆筒壁的对数平均半径。

其中：T∞，介质流体温度；T0，被加热物体初始温度；T，被加热物体中心的温度；t，物体加热时间；B，加热时间校正系数（与物性参数有关）。

如果被加热的物体为长方体，并且长方体的长宽高分别为a、b、c，则：

如果被加热物体为液体长方体（通过固体壁与加热介质隔开），则上述方程变为：

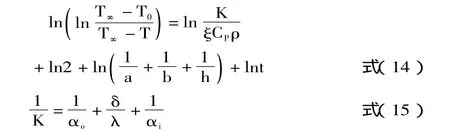
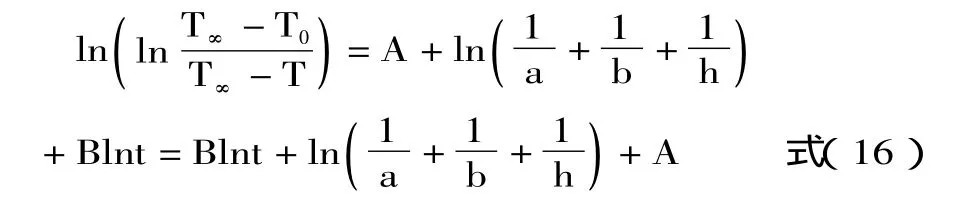
1.2.2 实验流程 调试数显恒温水浴锅→将装有纯净水（或牛奶、橙汁）的烧杯（或层析缸）封闭→烧杯（或层析缸）的中心安装温度计→进行不同温度的水浴加热→记录时间温度数据→换原料重复实验

2 结果与讨论

2.1 被加热物体为圆柱体

2.1.1 纯净水数据分析及计算 被加热物料为纯净水，纯净水充满圆柱体容器中并密闭，形成一个圆柱体整体，并置于水浴中加热，模拟杀菌过程。这种条件下的传热过程属于非稳态导热。

2.1.1.1 水浴温度为50℃的非稳态导热研究 实验的水浴温度50℃（T），圆柱体容器中的纯净水初温15℃（T0），圆柱体的半径为r=6.9975×10-2m，长为L=5.9000×10-2m，实验数据及计算见表1，圆柱体中心温度与加热时间的关系见图1，方差分析见表2。

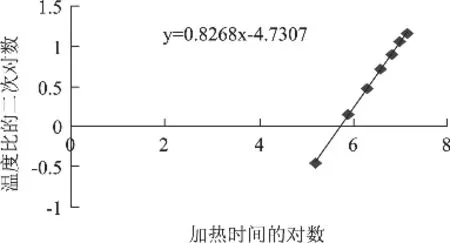
图1 温度与加热时间的关系

由F＞F0.05（1，5）可知，y与x之间的线性关系显著。

由y=0.8268x-4.7307，及式（10），即：

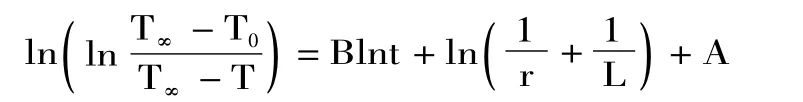
得：B=0.8268

解得：A=-8.1724

2.1.1.2 其它水浴温度下的常数值及平均常数值由同样的实验和数据处理方法，在水浴温度为60、70℃及平均温度下，被加热物体为圆柱体容器中的纯净水时，常数值见表3。

表4 被加热物体为圆柱体，且物料为牛奶、橙汁时公式中的常数

表5 纯净水在水浴杀菌过程中非稳态导热实验数据及计算

表6 方差分析表

表8 被加热物体为长方体，且物料为牛奶、橙汁时公式中的常数

表3 被加热物体为圆柱体，且物料为纯净水时公式中的常数

2.1.2 牛奶、橙汁数据分析及计算 牛奶或橙汁充满圆柱体容器中并密闭，形成一个圆柱体整体，并置于水浴中加热，这种条件下的传热过程属于非稳态导热。由同样的实验和数据处理方法获得的数据如表4所示。

2.2 被加热物体为长方体

2.2.1 纯净水数据分析及计算 纯净水充满长方体容器中并密闭，形成一个长方体整体，并置于水浴中加热，这种条件下的传热过程属于非稳态导热。

2.2.1.1 水浴温度为50℃的非稳态导热研究 实验的水浴温度50℃（T），长方体容器中的纯净水初温15℃（T0），长方体的长a=12.5×10-2m，宽b=8.5× 10-2m，高h=4.95×10-2m，实验数据及计算见表5，长方体中心温度与加热时间的关系见图2，方差分析，见表6。

图2 温度与加热时间的关系

由F＞F0.05（1，8）可知，y与x之间的线性关系显著。

由y=0.7362x-4.3798，及式（16），即：

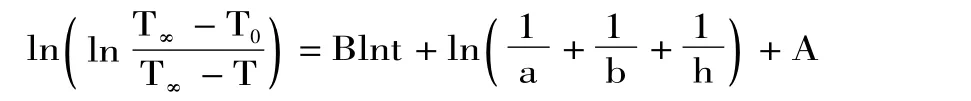
得：B=0.7362

解得：A=-8.0678

2.2.1.2 其它水浴温度下的常数值及平均常数值由同样的实验和数据处理方法，被加热物体为长方体容器中的纯净水时，水浴温度为60、70℃时的常数值及平均常数值见表7。

表7 被加热物体为长方体，且物料为纯净水时公式中的常数

2.2.2 牛奶、橙汁数据分析及计算 牛奶或橙汁充满长方体容器中并密闭，形成一个长方体整体，并置于水浴中加热。由同样的实验和数据处理方法获得的数据如表8所示。

3 结论

被加热物体为圆柱体的非稳态导热公式，当物料为纯净水时为式（17）；当物料为牛奶时为式（18）；当物料为橙汁时为式（19）。被加热物体为长方体的非稳态导热公式，当物料为纯净水时为式（20）；当物料为牛奶时为式（21）；当物料为橙汁时为式（22）。上述的公式为食品非稳态加热过程提供了较便捷的公式，在食品的生产及科研中有一定的应用价值。

［1］辛荣昌，陶文铨.非稳态导热充分发展阶段分析解［J］.工程热物理学报，1993，14（1）：80-81.

［2］杨能彪.一维非稳态导热问题的数值计算［J］.青海师范大学学报，2006（4）：24-26.

［3］孙昆峰，吴建波.非稳态导热初值问题稳定性条件的分析［J］.平顶山工学院学报，2004，13（4）：20-21.

［4］乔春珍，吴照云，项新耀.一维非稳态导热过程传递的规律及计算［J］.热科学与技术，2003，2（1）；42-45.

［5］徐林，金征宇，邓力.热敏电阻法测量食品导热系数的研究［J］.食品工业科技，2008，29（6）：114-116.

［6］杨同舟.食品工程原理［M］.北京：中国农业出版社，2003：181-183.

Study of unsteady heat conduction about liquid food

WU Da-wei，WU Di，NI Ting-ting
（Institute of Food Science and Techonology，Heilongjing Bayi Agriculture University，Daqing 163319，China）

Mathematics formula was found with the theory in unsteady heat conduction.Common liquid food like pure water，milk and orange juice as the material，they were contained and closed with vessels of long-square shape and cylinder shape，which was heated by the water of 50，60，70℃.The constants were determined with the data of the temperature and time.The formula of the relation of time and the centre temperature of cylinder shape and the long-square shape liquid food was obtained under the unsteady heat conduction.

liquid food；unsteady heat conduction；mathematics formula

TS201.1

A

1002-0306（2010）11-0138-04

2010-04-16

吴大伟（1971-），男，副教授，研究方向：食品工程。