TLD振动台子结构试验的数值仿真分析1

周惠蒙 吴 斌

（哈尔滨工业大学土木工程学院，哈尔滨 150090）

TLD振动台子结构试验的数值仿真分析1

周惠蒙 吴 斌

（哈尔滨工业大学土木工程学院，哈尔滨 150090）

本文采用振动台子结构试验数值仿真验证了圆柱形调谐液体阻尼器（CTLD）控制建筑结构地震响应的性能。振动台子结构试验将结构模型作为数值子结构在计算机中计算，将CTLD作为试验子结构进行物理试验。在CTLD和振动台之间安装剪切力检测装置，将测得的剪切力和地震波输入到数值子结构中，采用实时子结构中心差分法进行数值子结构运动方程的求解，计算得到了结构顶层的绝对加速度。再将加速度由振动台实时加载到试验子结构上，实现了结构和CTLD的相互作用。对一个单自由度结构有CTLD控制和无CTLD控制时的加速度响应进行了精确数值求解，结果验证了CTLD能够有效地控制结构在地震作用下的加速度响应。用振动台子结构试验对CTLD与结构耦合系统进行仿真，得到的加速度响应与精确数值求解的结果吻合较好，验证了这种方法能够准确地评估CTLD的减振性能。

地震模拟振动台 子结构试验 CTLD 中心差分法

引言

传统的拟动力试验方法和振动台试验方法存在一些缺陷，其主要表现为拟动力试验方法反映的是慢速加载下试件的抗震性能，不能够反映速度相关型和加速度相关型试件的抗震性能。而受振动台承载力的限制，一般的振动台试验只能进行缩尺的模型结构试验，由于缩尺结构模型的动力相似比很难满足要求，尤其是在弹塑性范围内，所以试验结果难于推广到原型结构中去。1992年，Nakashima等（1992）提出了实时子结构实验方法，这种方法对速度相关型试件进行实时加载以准确获得其性能，自此之后，我国学者也对此试验方法展开了一系列研究（袁涌等，2008；李进等，2005），并已应用在实际工程中（Wu等，2007）。这种试验方法主要针对速度相关型试件，它将结构分为数值子结构与实验子结构，将呈现复杂非线性的结构部分作为试验子结构，由物理试验模拟；将结构其它部分看成是线性的，作为数值子结构，由计算机模拟；由作动器或振动台等加载装置的实时加载来使两部分交界面处的变形一致，作用力平衡。

TMD和TLD等结构控制装置是加速度相关型试件，它们的减振性能与其底部受到的加速度密切相关，一般采用振动台进行试验。Igarashi等（2002）对一个65m高的桥墩TMD进行了振动台子结构试验，同时国外的一些学者已经在振动台子结构方面进行了很多工作（Horiuchi等，2000；Reinhorn等，2004）。Lee等（2007）对RTLD进行了振动台子结构试验，采用的是状态方程方法对数值子结构进行求解，但没有深入分析积分算法对加速度实现的影响。杨现东等（2007）对考虑质量的动力子结构提出了实时子结构中心差分法，实现了动力子结构加速度的准确控制。

本文采用考虑质量的实时子结构中心差分法，对CTLD和结构耦合系统进行振动台子结构试验，以验证这种方法在评估CTLD控制建筑结构的地震加速度响应性能中的准确性。

1 振动台子结构试验概述

1.1 振动台子结构试验原理

图1是对一个顶层安装了CTLD阻尼器的3自由度结构的振动台子结构实验的原理图。

图1 振动台子结构实验的原理框图Fig.1 Layout showing the principle of substructure shaking table

振动台子结构试验方法将顶层安装了CTLD的结构分成两部分：下部的结构主体作为数值子结构；上部的CTLD作为试验子结构。对CTLD作为物理试件安装在振动台上进行试验，受到TLD施加的剪切力和地震波作用的数值子结构在控制振动台运动的计算机中进行计算。计算得到的结构顶部绝对加速度通过振动台施加到CTLD上，安装在CTLD和振动台台面之间的剪切力测量装置测量其产生的剪力，将得到的剪力输入到计算机中，对数值子结构的方程进行求解，得到下一步的结构顶层加速度后再由振动台加载。

数值子结构的运动方程为：

1.2 考虑试件质量的实时子结构中心差分法

为了使用控制计算机实时计算数值子结构运动方程，采用考虑质量的实时子结构中心差分法（杨现东等，2007）对式（1）进行求解，可以得到第i+1积分步的位移为：

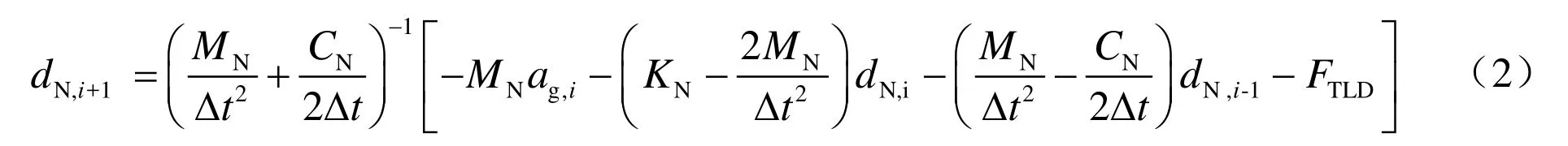
试验加载时假定试验子结构在一个积分步长内加速度为常数，考虑到TLD产生的剪力与其受到绝对加速度输入有关，位移命令发送按下式确定：

式中，ag,i+1为第i+1积分步的地面运动的加速度。为目标相对加速度，按下式计算：

试验中可以把目标位移信号分为一系列的位移信号在一个积分步长内依次发送给作动器。其中确定，是位移信号的采样时间间隔。这样可以保证在一个积分步长内作动器所实现的加速度为常数。

2 试验系统建模

为了进行振动台子结构试验的仿真，需要对振动台加载系统和试验子结构（CTLD水箱）进行数学建模。

图2 振动台子结构实验系统示意图Fig.2 Flowchart of experiment of substructure shaking table

2.1 振动台子结构试验系统

图2是振动台子结构试验系统的示意图。图中的地震模拟振动台作为加载设备，试验子结构是CTLD水箱，数值计算在计算机（MTS公司的FlexTest GT控制器）中完成。振动台剪切力由安装在CTLD和振动台中间的剪切力测量装置测量，如图3所示。

图3 剪切力测量装置示意图Fig.3 Sketch map of shear force measurement

对测量得到的上台面和CTLD共同产生的剪力以及上台面的加速度进行计算，由于上台面的质量已知，因此可将总剪力减去上台面的惯性力即可得到CTLD产生的剪力。其计算公式为：

2.2 振动台系统建模

采用哈尔滨工业大学力学与结构试验中心的单自由度地震模拟振动台作为加载设备，对TLD水箱输入数值子结构计算得到的结构顶层的绝对加速度进行计算。首先采用邱法维（1989）建立的单自由度振动台模型分析振动台系统的动态性能。根据潘景龙（1990）分析得到的台面支撑系统产生的扰力和振动台基础的振动十分微小，所以不考虑振动台基础的动力特性，可忽略振动台台面受到的扰力。由于试验子结构（CTLD水箱）的质量大约是29kg，远小于振动台台面自重，因此不考虑负载对振动台系统特性的影响。建立振动台系统的模型如图4所示。

图4 电液伺服地震模拟振动台的控制系统框图Fig.4 Flowchart of shaking table test with tuned liquid

由于单独采用位移反馈控制时，振动台的响应存在一定的时滞，不能够满足实时试验的要求。为了提高振动台的响应速度，采用加速度反馈和速度反馈来改善系统的稳定性并扩展使用频率范围，这样可提高系统的动态响应性能（黄浩华等，1981）。同时，采用Jung等（2006）使用的前馈环节来减少系统响应时滞（图4）。系统的闭环传递函数为：

式中，Kf为调节器增益（即位移反馈增益）；Kp、Ki、Kd和Kff分别为控制器比例、积分、微分和前馈增益；Wy(s)为伺服阀和作动器的传递函数；H(s)是反馈环节的传递函数。

Wy(s)的表达式为：

式中，mt为台面质量；Α为活塞有效面积；Vt为缸的体积；βe为油的弹性模量；kc为伺服阀压力流量增益；ka为电压电流转换系数；ksv为伺服阀的流量增益。

H(s)的表达式为：式中，Kf为位移反馈增益；Kv为速度反馈增益；Ka为加速度反馈增益。

以上伺服阀和位移反馈参数采用邱法维（1989）列出的参数。

2.2 CTLD建模

为了进行试验的仿真，需要对CTLD建模，通过数值计算来求得振动台子结构试验中CTLD产生的剪力。

固定在结构顶层的CTLD晃动时，水发生波动产生控制力。当水的波动较小时，可以采用等效线性模型（吴波等，1997），只考虑水晃动的第一振型时，W(t)（可以理解成波高）满足如下微分方程：

CTLD对结构的控制力为：

由数值子结构计算出顶层的绝对加速度通过振动台输入到CTLD的底部。再由式（9）和式（10）就可以得到CTLD产生的剪力。可以看出，CTLD底部产生的剪力是与加速度相关的。

3 试验验证

3.1 振动台性能试验

为了验证振动台系统能够实时实现加速度命令，首先通过单步加载试验来验证系统的动态响应特性能够满足实时试验的要求。

采用PID控制器同时引入前馈控制，控制参数为：Kp=145，Ki=0，Kd=0.06，Kff=0.5。已知位移反馈增益Kf=80，引入加速度反馈和速度反馈，加速度反馈增益与速度反馈增益分别为Ka=0.001、Kv=0.5。首先输入单步阶跃命令，得到响应如图5所示。

图5 振动台台面位移阶跃响应Fig.5 Plot of respond of shaking table

图6 指令插值发送时振动台台面的加速度阶跃响应Fig.6 Acceleration respond of shaking table

从图5可以看出，系统的响应时滞为10ms左右，已知积分步长Δt=0.01s，所以在一个积分步长内能够达到目标位移。所以通过调整控制参数，并引入速度、加速度反馈和前馈控制，振动台系统有足够的响应速度来满足实时试验的需要。

3.2 加速度控制验证

为了保证在实时试验中，施加到试验子结构上的加速度与数值子结构计算得到的加速度一致，按1.2节在试验中把目标位移信号分为一系列的位移信号在一个积分步长Δt内依次发给作动器。积分步长为Δt=0.01s，j0=10，分10次插值发送。目标加速度假设为1，分析台面加速度在一个积分步长内实现的情况如图6所示。

从图6可以看出，在积分步长末振动台实现了加速度命令，通过对积分步长内位移命令10次插值发送，能够在积分步长内实现加速度命令，因此积分算法能够准确地实现CTLD底部的加速度加载，满足振动台子结构试验的要求。

3.3 CTLD的抗震性能验证

为了验证试验方法，对一个顶部装有CTLD的单自由度结构进行振动台子结构试验仿真。这个结构原型是取自Haneda机场安装CTLD装置的空中交通控制塔（Tamura等，1995），它安装了1404个CTLD，取出其中一个作为实验子结构，将其剪力乘以1404作为所有CTLD装置对下部结构产生的剪力。对原型结构进行简化，取此结构的基本振型参数作为数值子结构的参数：MΝ=6.48571× 105kg ，KΝ=1.5064× 104kN/m ，CΝ=52.51kN⋅ s/m，结构的自振频率fs=0.77Η z。水箱的底面半径a=0.3m，按照CTLD的设计方法（Soong 等，2005），取水的高度h=0.053m 。CTLD中水晃动的基频fΤ=0.74Η z与最优的调谐频率比较接近，符合TLD调谐的要求。

首先进行精确数值计算（使用LISM微分求解器进行计算，采样周期为0.001s），得到无CTLD控制和有CTLD控制时的结构在地震作用下的加速度响应，并对两者所得到的结构加速度响应曲线进行比较，分别从时域和频域方面来比较结构绝对加速度响应，如图7和图8所示。输入的地震波峰值加速度为200gal，并分别将EI Centro、Taft、Kobe和Tian Jin地震波记录作为地震动输入。

从图7可以看出，有CTLD控制时，结构的加速度响应在后阶段减少十分明显。这与TMD类耗能减振装置减振曲线的特征是一致的，因为地震波到来的冲击使CTLD中的水形成波动，从而产生剪力来控制结构的地震响应。从图8可以看出，频域曲线是由整个加速度响应时程信号经过傅立叶变换得到的各个频率的响应幅值，在结构自振频率附近加速度响应的幅值减少到50%。仿真结果表明，CTLD能够较好地控制结构的加速度响应。

然后，进行CTLD的振动台子结构试验方法的仿真。将下部结构作为数值子结构，CTLD作为试验子结构，振动台子结构试验系统如图2所示。图9和图10分别从时域和频域比较了使用振动台子结构和精确计算模型得到的结构加速度响应信号。从中可以看出，采用振动台子结构方法仿真得到的数值子结构绝对加速度响应，与采用MATLAB的LISM命令计算有CTLD结构的绝对加速度响应比较，发现两者波形吻合得很好，证明了振动台子结构方法的有效性。El Centro和Taft地震波得到的加速度响应在地震动开始阶段有细微误差，这可能是由振动台加速度控制的时滞引起的，由于这2个地震波加速度突变发生较早，所以时滞引起的误差较明显。MATLAB的LISM命令计算得到的绝对加速度响应与振动台子结构试验仿真得到的绝对加速度响应均方根的比较如表1所示，从表中可以看出，对应不同的地震波，两种方法得到的绝对加速度响应的均方根之间的误差为0.001(m/s2) —0.013(m/s2)，两者的结果吻合较好。仿真结果表明，振动台子结构实验能够准确地评估CTLD控制结构在地震作用下的加速度响应性能。

图7 结构绝对加速度响应时域曲线（实线：有控制；虚线：无控制）Fig.7 Acceleration time history curves with (solid lines) and without (dashed lines) control

图8 结构绝对加速度响应的频域曲线（实线：有控制；虚线：无控制）Fig.8 Acceleration frequency history curves with (solid lines) and without (dashed lines) control

图9 被控结构加速度响应时域比较（虚线：LISM计算；实线：子结构试验仿真）Fig.9 Comparison of acceleration time history curves between numerical model (dashed lines)and shaking table test (solid lines)

图10 被控结构加速度响应频域比较（虚线：LISM计算；实线：子结构试验仿真）Fig.10 Comparisons of controlled structural absolute accelerations in the frequency domain (dotted line: LISM calculation, solid line: substructure testing simulation)

表1 不同计算方法得到的被控结构加速度响应均方根（单位：m⋅s−2）Table 1 Average square roots of accelerations of structures with different TLD control

4 结论

对CTLD与结构耦合系统进行了振动台子结构实验仿真。采用加速度反馈和速度反馈，提高了振动台系统的动态性能，同时采用前馈环节减少了系统时滞，使振动台系统能够满足实时试验的需要。对CTLD与结构耦合系统控制加速度响应性能进行了振动台子结构试验仿真，仿真结果与模型精确计算的结果吻合很好，证明振动台子结构试验能够准确地评估CTLD控制结构加速度响应的性能。通过顶部安装CTLD的单自由度结构控制的加速度响应仿真表明，CTLD能够有效地控制结构物在地震作用下的加速度响应。

黄浩华，徐文德，1981．位移控制电液伺服系统特性的改善方法．液压与气动，（1）：5—8.

李进，王焕定，张永山，赵桂峰，2005．高阶单步实时动力子结构试验技术研究．地震工程与工程振动，25（1）：97—101.

潘景龙，1990．单向模拟地震振动台设计中的若干问题讨论．哈尔滨建筑工程学院学报，23（2）：90—99.

邱法维，1989．电液伺服地震模拟振动台模拟控制系统理论分析．哈尔滨建筑工程学院学报，22（3）：100—111.

吴波，李惠，1997．建筑结构被动控制的理论与应用．哈尔滨：哈尔滨工业大学出版社，70—85.

袁涌，熊世树，朱宏平，2008．加载速率对速度控制型实时子结构拟动力实验结果的影响．东南大学学报(自然科学版)，5（38）：784—787.

杨现东，邓利霞，吴斌，2007．考虑试件质量的实时子结构试验中心差分法．见：第六届全国结构减震控制学术研讨会．昆明.

Horiuchi T., Inoue M., Konno T., 2000. Development of real-time hybrid experimental system using a shaking table.See: Proc. 12th Word Conference on Earthquake Engineering．paper No.0843.

Igarashi A., Iemura H., Tanaka H., 2002. Development of substructure hybrid shake table test method and application to verification tests of vibration control devices. See: China-Japan workshop vibration control and health monitoring of substructures and third Chinese symposium on structural vibration control. Shanghai,China.

Jung R.Y., Shing P.B., 2006. Performance evaluation of a real-time pseudodynamic test system. Earthquake Engineering and Structural Dynamic, 35: 789—810.

Lee S.K., Park E.C., Min K.W., Lee S.H., Chung L., Park J.H., 2007. Real-time hybrid shaking table testing method for the performance evaluation of a tuned liquid damper controlling seismic response of building structures.Journal of Sound and Vibration, 302: 596—612.

Nakashima M., Kato H., Takaoka E.,1992. Development of real-time Pseudo dynamic testing. Earthquake Engineering and Structural Dynamics, 21(1): 79—92.

Reinhorn A.M., Sivaselvan M.V., Liang Z., Shao X.Y., 2004. Real-time dynamic hybrid testing of structural systems.See: Proc 13th Word Conference on Earthquake Engineering．paper No.1644.

Soong T.T., Dargush G.F.著, 董平译，2005. Passive Energy Dissipation Systems in Structural Engineering (结构工程中的被动消能系统). 北京：科学出版社，212—239.

Tamura Y., Fujii K., Ohtsuki T., Wakahara T., Kohsaka R., 1995. Effectiveness of tuned liquid dampers under wind exicitation. Engineering Structures, 17(9): 609—621.

Wu B., Wang Q., Sing P.B., Ou J., 2007. Equivalent force control method for generalized real-time substructure testing with implicit integration. Earthquake Engineering and Structural Dynamics, 36: 1127—1149.

Numerical Simulation of Substructure Shaking Table Test with Tuned Liquid Damper

Zhou Huimeng and Wu Bin
(School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China)

Substructure shaking table method was applied for evaluating the seismic performance of a circle tuned liquid damper in a structure. The CTLD was chosen to be the experimental substructure tested physically, and the other structures were chosen to be the numerical substructures simulated in a computer. The seismic wave and the shear force measured by the sensor installed between the shaking table and the CTLD were input to the numerical substructure. With the central difference method for Real-time substructure testing considering specimen mass, the absolute acceleration at the top lay of the structure was calculated. This acceleration was enforced to the experimental substructure in real-time by shaking table in order to realize the interaction between the CTLD and structure. It is shown from pure numerical simulations for a SDOF system with and without CTLD control that the CTLD can effectively control the acceleration response of a structure. Then, Numerical simulations with the substructure shaking table method for a SDOF system with control were conducted and the results show that the acceleration response matches the pure numerical simulation result very well. This means that this method can effectively evaluate the seismic performance of the circle tuned liquid damper.

Shaking table substructure test; CTLD; Central difference method

国家自然科学基金（90715036、50938001），地震行业科研专项经费（20084190731）

2010-02-09

周惠蒙，男，生于1982年。博士生。主要从事结构试验技术研究。E-mail: Zhouhuimeng@hit.edu.cn吴斌，男，生于1970年。教授，副院长。主要从事结构控制和结构试验技术研究。E-mail:bin.wu@hit.edu.cn

周惠蒙，吴斌，2010. TLD振动台子结构试验的数值仿真分析. 震灾防御技术，5（1）：9—19.