船撞桥概率模型的比较与选用

唐 勇, 金允龙, 赵振宇

(上海船舶运输科学研究所运输系统事业部,上海200135)

0 前 言

在我国,随着交通运输业的不断发展,跨海跨江河的大型桥梁越来越多。与此同时,全世界的船舶也正向大型化、高速化发展,其流量和吨位都不断增加,这使得船桥碰撞的灾难性事故日益增多。船撞桥事故不仅会带来巨大的经济损失,而且还会导致大量的人员伤亡和环境破坏,造成负面的社会影响。

船桥碰撞安全评估的核心内容之一就是桥梁遭受船舶撞击概率的计算,为了研究船舶撞击桥梁的风险概率,一批碰撞概率模型相继诞生。概率模型主要采用统计分析方法和数学模型方法,其中最具代表性的有:AASHTO模型、KUNZI模型和三概率参数积分路径模型(改进的KUNZI模型)。

1 各模型特点介绍

1.1 AASHTO模型[1]

《美国公路桥梁防船撞设计指南》(2009)给出了桥梁各桥墩年倒塌频率的计算公式

式中:N为船舶年通航量;PA,PG,PC分别为偏航概率、几何概率和倒塌概率。其中,公式中去除PC后便是桥梁遭受船舶撞击的年频率。

偏航概率PA按式(2)进行计算

式中:BR,RB,RC,RXC,RD分别为偏航基准概率、桥位修正系数、平行水流修正系数、横流修正系数和船舶交通密度修正系数。

几何概率PG的计算如图1所示。AASH TO模型采用正态分布来模拟船舶的分布,均值为航道的中心线,标准差为船舶的典型长度。

1.2 KUNZI模型[3]

1998年,德国的昆兹(C.N.Kunz)根据船撞桥事故发生前船与桥墩的相互位置为基础,建立了一个具有两随机参数的船桥碰撞概率计算模型。第1个随机参数为船舶的偏航角度φ,第2个随机参数为停船距离x。偏航角度φ是指船舶航行方向与预定的航线方向之间的角度,见图2。

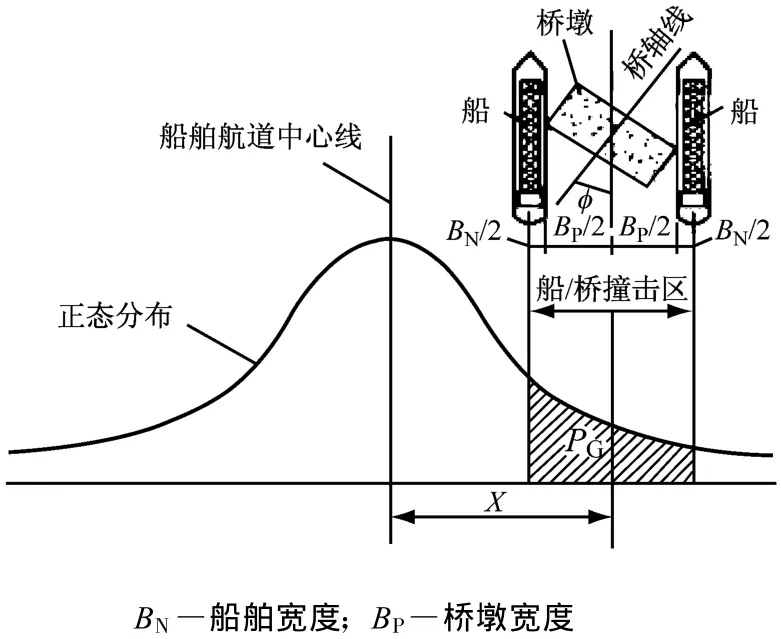
图1 AASHTO几何概率PG计算示意图

图2 KUNZI船桥碰撞概率模型

对于φ和x,KUNZI模型中采用正态分布来对其进行描述,即

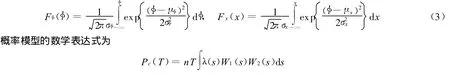
式中:W1(s)=Fφ(φ1)-Fφ(φ2)是一条撞击航迹的概率;W2(s)=1-Fx(s)是撞击前事故未得到制止的概率;λ(s)是船舶单位航行距离的失误概率。

1.3 三概率参数积分路径模型(改进的KUNZI模型)

文献[2]针对KUNZI模型中的不足之处,提出了改进的KUNZI模型。改进的KUNZI模型主要特点为:在原KUNZI模型的基础上,增加1项积分来考虑船舶横向分布(几何分布)对碰撞概率的影响,使模型的理论推导更加符合实际情况。

为了考虑船舶航迹横向(几何)分布对碰撞概率的影响,改进的KUNZI模型如图3所示,船舶自原点航行到桥墩处的距离为D,也即积分路径长度为D,D可取≥μs+3σs(μs为停船距离均值;σs为停船距离标准差)。X,Y为船舶在航行过程中的积分坐标。

经改进的KUNZI模型积分式为

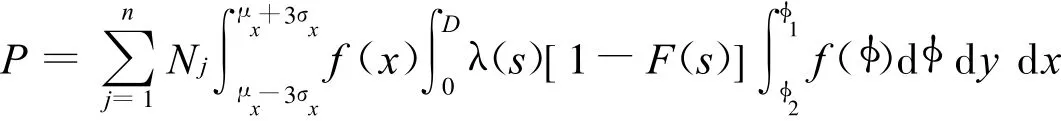
式中:

P——年碰撞频率;

N j——按船舶分类方法第j种船舶的年通航量,艘次;

W1(s)——一条撞击航迹的概率,W1(s)=Fφ(φ1)-Fφ(φ2);

W2(s)——撞击前事故未得到制止的概率,W1(s)=1-Fx(s);

μx——船舶的航迹横向分布(几何分布)均值;

σx——船舶的航迹横向分布(几何分布)标准差。

根据船舶航迹所处的横向位置不同,分A,B,C区来确定KUNZI模型中的积分上下限φ1,φ2(见图4)。

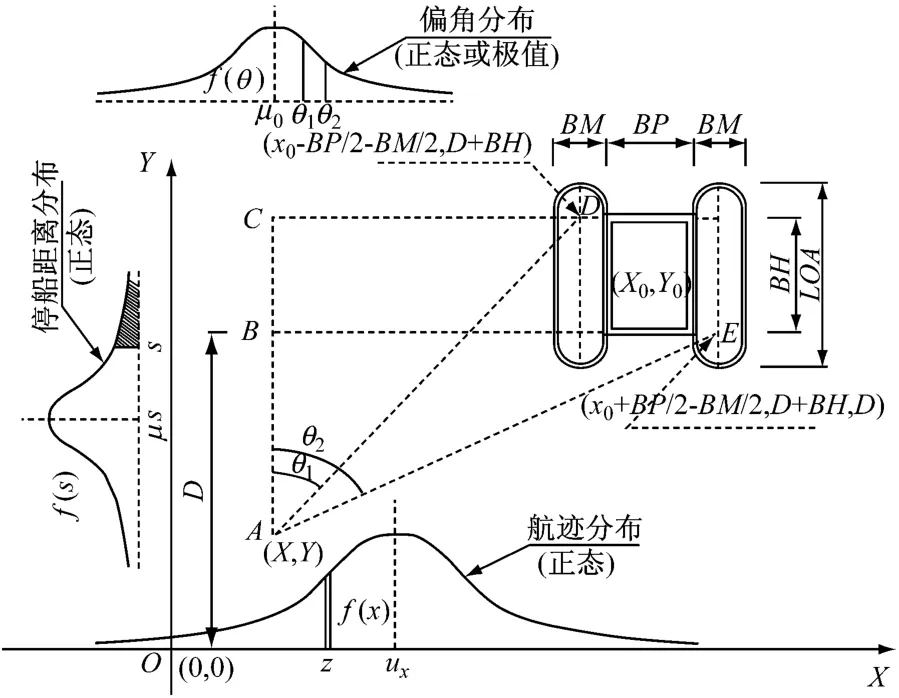
图3 三概率参数积分路径模型计算示意图

图4 不同积分上下限的区间划分

2 三概率参数积分路径模型算例

2.1 桥型简介

以拟建的我国沿海某跨海大桥为例来进行船桥碰撞概率分析,大桥通航等级:500 t级杂货船;通航净空:125 m×17.5 m;大桥主通航孔:单孔双向通航(见图5)。

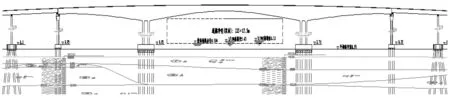
图5 大桥主桥立面布置图

2.2 碰撞概率分析的基本条件

1.桥区通航船舶现状和代表船型。由于受航道水深的限制,目前经过大桥桥区航道的船舶主要是乘潮通行的渔船和运输砂石料的货船,吨位较小,基本在500 t级以下,年预计流量和代表船型分别见表1,表2。

2.船舶过桥航迹及各桥墩位置图(详见图6,图7)。

3.各桥墩承台尺寸大小。主墩承台尺寸为20 m×18 m,过渡墩承台尺寸为10 m×6 m,引桥墩承台尺寸为10 m×10 m。

2.3 碰撞概率的参数分析

1.船舶航迹均值和方差。根据桥区年平均风速和常年流速低的特点,现假设这样一种理想状态,即桥区的风速、流速均假定为静止。由此,船舶在排除风速和流速等外界影响的条件下,一般按照航道中心线行驶,则航迹均值μx取0。同时,由于船舶在航道中心线与航道边缘之间均属于正常航行范围,故拟航迹方差σx取32 m 。

2.船舶偏航角均值和方差。林铁良[4]通过调查发现,多数情况下,μφ取0。而σφ取值和多种影响因素有关,船舶类型不同,σφ的大小也不同,基本集中在6.3°～30°。本算例 σφ取10°。

3.船舶停船距离均值和方差

1)停车冲程经验估算式。主机停车操作,从操作时起一直至船舶停止的过程中,某一时刻t的船速V及其在此期间船舶滑行的距离S为

式中:C为减速时间常数(船舶停车后船速每递减1/2所需的时间),单位为min,C值随船舶排水量的不同而不同(排水量≤1 000 t时,C=1);速度单位为kn;距离为n mile;时间为min。

本算例中,船舶过桥航行速度为9 kn,减速时间常数C=1,则

2)停车冲程实船数据。引用《船舶交通工程学》[5]中船舶的运动性能统计资料,见表3。

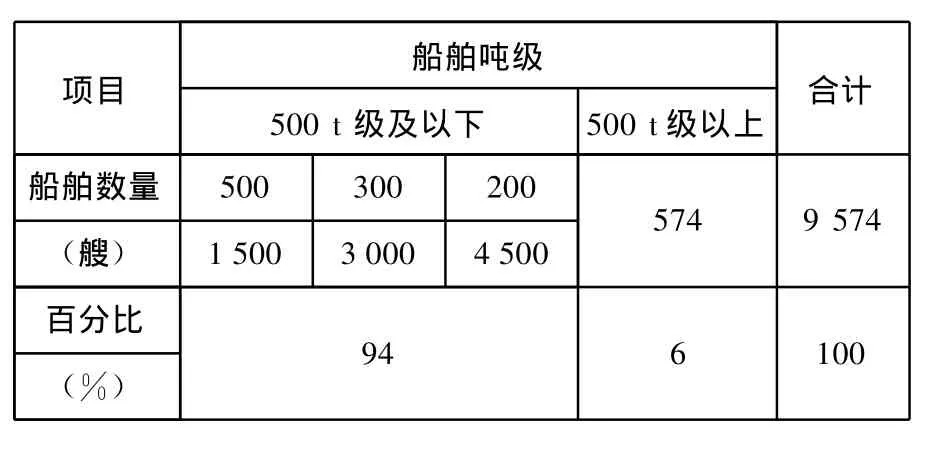
表1 桥区水域船舶年预计流量统计

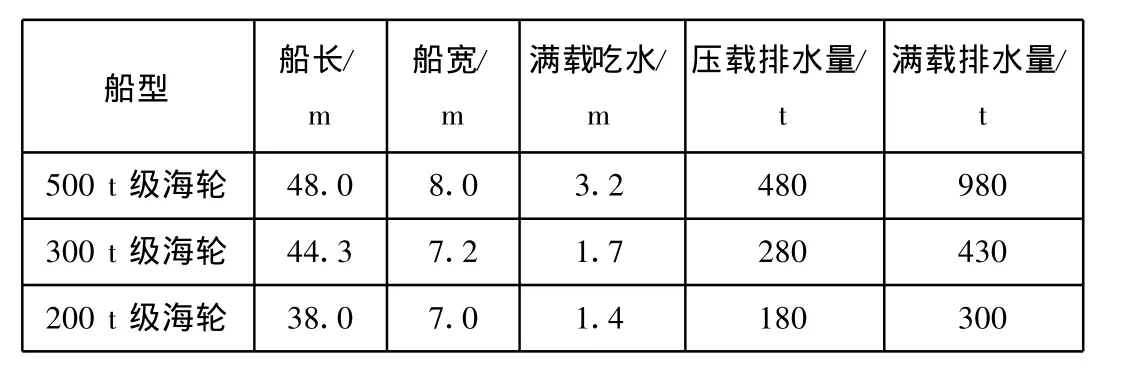
表2 桥区通航代表船型

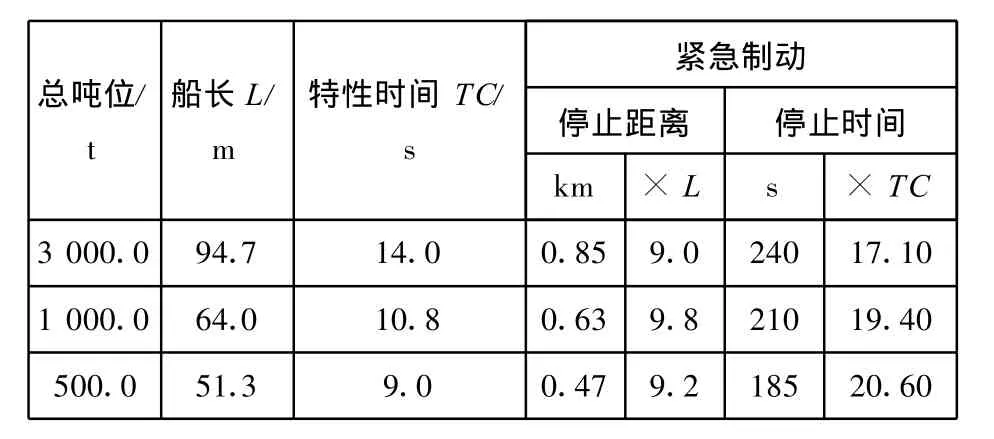
表3 船舶的运动性能

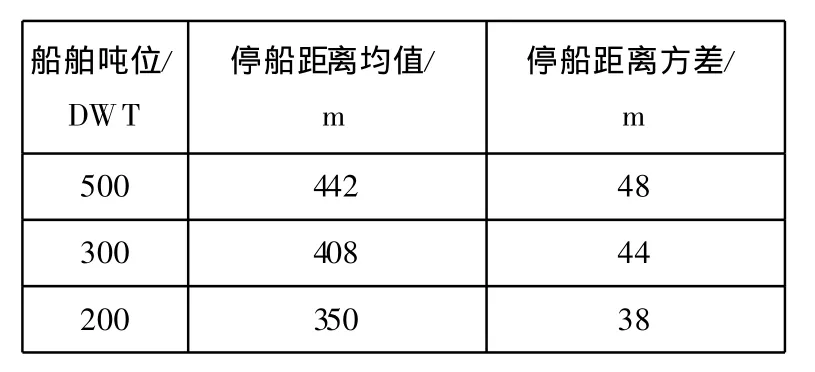
表4 停船距离均值/方差

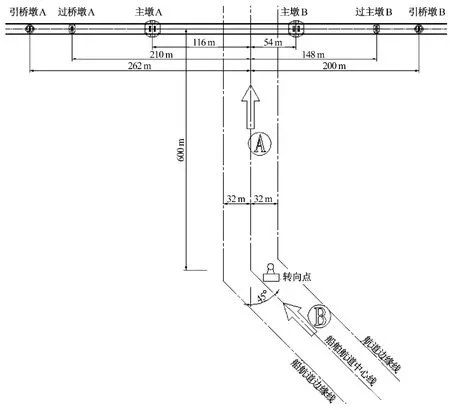
图6 船舶航迹及各桥墩位置图

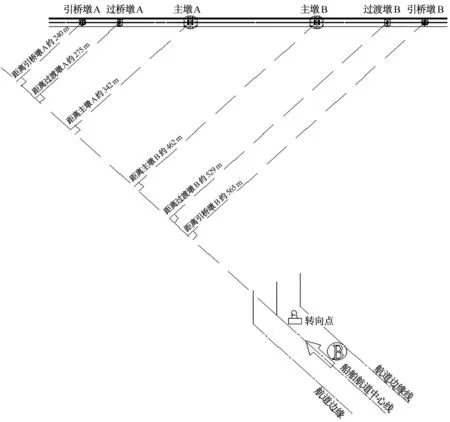
图7 航道B距离各桥墩位置图

3)基于桥梁安全因素考虑,本算例取停车冲程实船数据(9.2L)。此外,由于船舶在顺水和逆水航行时的停车冲程会有所不同,一般在流速较低时,停车冲程差与船舶自身船长接近,因此,本算例拟停船距离方差取为1.0L,具体数据见表 4。

4.积分路径长度,即为船舶自原点航行到桥墩处的距离为D,也即积分路径长度为D。例如,500 t级海轮 D≥μs+3σs=442+3×48=586 m。

5.船舶单位航程事故率,一方面与船舶自身息息相关,另一方面又与桥区环境密不可分,诸如风速、流速。所以,λ(s)必定是一个多参数相互影响的函数。但由于国内缺乏相关资料和系统的调查研究,因此,根据AASHTO规范建议,船舶偏航概率PA为

PA=BR ×RB×RC×RXC×RD

本算例中,BR=0.6×10-4,RB=2.0,RC=1.02,RXC=1.27,RD=1.3,则 PA≈2.0×10-4。此外,由于桥区通航船舶吨位较小,停船冲程较短,因此涉及到风险分析范围内的航道长度拟取为1 000 m,则可得出λ(s)=2.0×10-4/1 000=2.0×10-7艘/m。

2.4 碰撞概率的计算结果

以三概率参数积分路径模型计算桥梁主墩碰撞概率为例:

3 计算结果分析

3种概率模型计算结果汇总如表5,具体数据比较见图8。

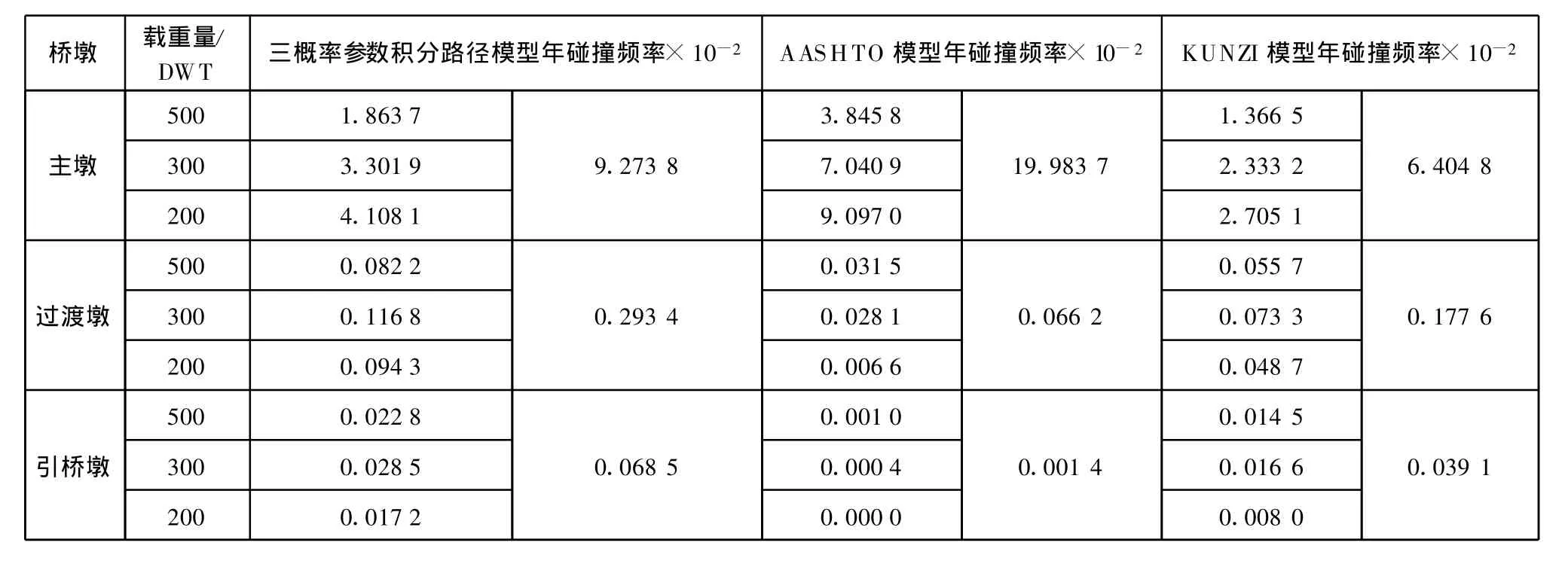
表5 3种概率模型计算结果汇总

数据分析如下:

1.对桥梁主墩而言,AASH TO模型的计算结果均大于三概率参数积分路径模型和KUNZI模型,但三者属于同一数量级;

图8 3种概率模型计算结果比较

2.对过渡墩和引桥墩而言,AASHTO模型的计算结果均小于三概率参数积分路径模型和KUNZI模型。其中引桥墩的碰撞概率远小于后二者;

3.三概率参数积分路径模型的计算结果均大于KUNZI模型的结果。

4 主要结论

1.三概率参数积分路径模型通过增加一项积分来考虑船舶横向分布后,其计算出的碰撞概率大于KUNZI模型,说明船舶横向分布的影响因素较为显著,提高了桥梁受船舶撞击的概率风险。因此,三概率参数积分路径模型与现实的船撞桥情况更为接近。

2.船舶单位航行距离的失误概率λ(s)影响因素很大,其取值直接决定三概率参数积分路径模型和KUNZI模型的计算结果大小,因此,对λ(s)开展深入的调查研究很有必要。

3.桥区水域船舶年通航量的预测存在不确定性,要正确预测20至30年后的船舶年通航量是相当困难的。另外,船舶通航量在时间域上存在着不均匀性,高密度的通航量必将会增加船舶撞击桥梁的风险。因此,船舶年通航量的预测必须与当地的经济社会发展紧密联系。同时,对船舶通航量应进行分时间段/分季节观测,丰富船舶通航量数据库的信息。

4.AASHTO模型为经验公式,且其中的参数多为统计型参数,统计数据主要针对桥梁的主墩,过渡墩和引桥墩的计算结果误差较大。同时,由于未考虑诸如风、能见度条件、助航设施等影响因素,故其计算结果往往偏大。

5.由于三概率参数积分路径模型为纯粹的数学模型,而实际上,综合考虑桥区环境和特定通航船舶的操纵性能和发生事故率等因素是相当复杂的。因此,基于桥梁的充分安全,建议选用AASHTO模型和三概率参数积分路径模型分别对桥梁的各个桥墩进行碰撞概率的计算,取两者的较大数值作为该桥墩的碰撞概率。

[1] AASHTO.Guide specification and commentary for vessel collision design of highway bridges[M].Second Edition.Washington D.C.:American Association of State Highway and Transportation Officials,2009.

[2] 耿波,汪宏.船桥碰撞概率计算模型研究[C]//交通部西部交通建设科技项目管理中心.2007年交通资源节约和环境保护新技术研讨会交通资源节约和环境保护新技术研讨会论文集.重庆:人民交通出版社,2007:212-220.

[3] Kunz C U.Ship bridge collision in river traffic[C]//Analysis and Design Practice.Ship Collision Analysis.Denmark:Balkema,Rotterdam,1998.

[4] 林铁良.船撞桥偏航角分布研究[J].结构工程师,2007,23(1):31-37.

[5] 邱民.船舶交通工程学[M].北京:人民交通出版社,1992.