不可导点的一些注记
谷振涛白俊霞刘琦
1.山东英才学院基础教学部 250104;2.胶南市科学技术局 266400
不可导点的一些注记
谷振涛1白俊霞1刘琦2
1.山东英才学院基础教学部 250104;2.胶南市科学技术局 266400
对于高等数学中求极值或最值部分,需要研究函数在定义域内的不可导点,来确定其是否为极值点或最值点。因此,如何快速来确定函数在哪些点不可导就显得尤为重要。该文对于如何快速确定函数的不可导点给出了一些办法。
不可导点;导数;最大值
高等数学中无论是求极值、最值还是判断单调区间都需要考察函数的不可导点。如何快速准确地判定所考察的函数在哪些点不可导,这需要一些行之有效的办法,而不能仅靠直觉。
1、用导函数的定义域来判定不可导点
当x≠0时,函数的导数为
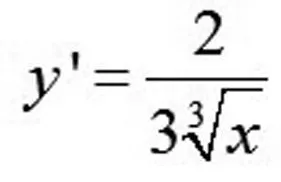
当x=0时,函数的导数不存在.在(-∞,0)内,y’<0,因此函数在 (-∞,0]上单调减少.在(0,+∞)内,y’> 0,因此函数在[0,+∞)上单调增加。
在上例的求解过程中通常教材中都不会具体给出如何判定x=0是不可导点,可以默认通过定义进行判断该点不可导。
2、用导数的定义来判定不可导点
这种判定方法显得直接,而容易操作,但是这里也有一个难点,如何先判定哪些点可能是不可导点,然后才能对这些可疑的点用导数定义来判断在该点函数是否可导。这里的预先划定怀疑范围也会带来一些麻烦,如果可疑点是可导点,则似乎我们做的定义判别是无用功,因此用导数定义来判断一个点是否是可导点,针对一些具体的题目是可以的.但是通常在一些较为综合的题目中,这个方法就显得很笨拙。
解 利用导数的定义
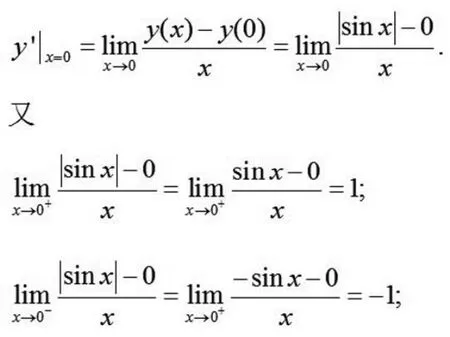
下面看一个较为综合的题目。
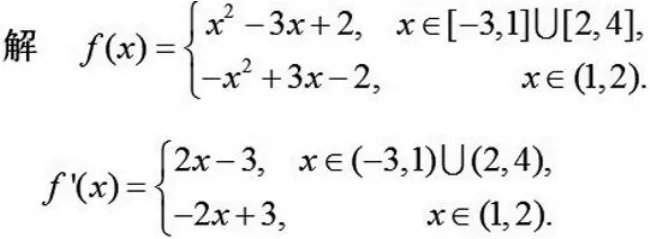
在这个题目中,我们其实可以凭直觉,得到x=1,x=2很可能是不可导点,然后可以用定义来判定其是否为不可导点。
但是在这样一个综合性的题目中,我们用定义来判定不可导点,显得既麻烦,又没有效率,但是求最大值的规则要求我们必须验证这些点的身份。(当然这个题目我们为了求得最值,不需要验证x=1, x=2是否可导点,直接将其作为可疑最值点与端点和驻点进行比较即可)。
我们自然寻求一些便于判断函数不可导点的快捷办法。
3、假想延拓法判定不可导点
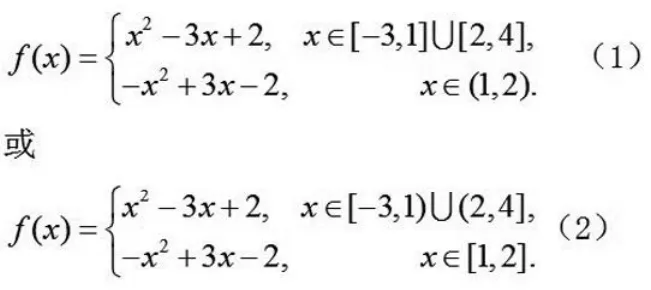
讨论函数在x=1处是否可导,利用(1)式.我们假想
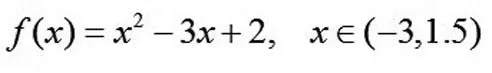
则其在(-3,1.5)上的导函数为f’(x) =2x-3。当然导函数在x=1处的形式也是f’(x)=2x-3,因此立即得知函数f(x)=x2-3x+2在x∈[-3,1]左可导,且
利用(2)式,假想
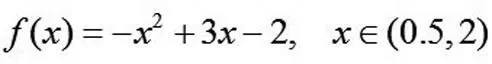
则在(0.5,2)上的导函数为f’(x) =-2x+3。当然导函数在x=1处的形式也是f’(x)=-2x+3,因此,立即得知函数f(x) =-x2+3x-2,x∈[1,2]在x=1右可导,且。
于是我们得到在x=1处左右导数存在不相等,因此函数在x=1处不可导,类似可得函数在x=2处也不可导。
注意:虽然假想延拓法看似复杂,但是理解其内涵之后,运用起来相当简单,另外假想延拓法也要注意一些条件,比如函数在所讨论点连续,在该点的左右邻域里均是初等函数。
4、关于以上方法的比较应用
例4 设函数
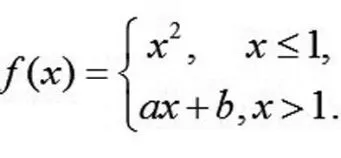
为了使函数f(x)在x=1处连续且可导,a,b应该取何值。
解法一:据已知f(x)在x=1处可导,因此
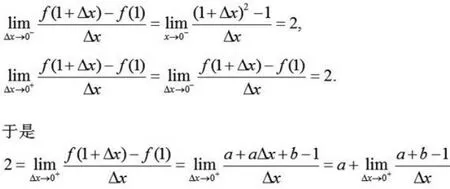
因而必有a+b-1=0以及a=2,由此解得b=-1。
解法二:据已知函数在x=1处连续且可导,因此在x=1处左右导数均存在.根据假想延拓法知函数在x=1处左导数为f’_(1)=2,于是再根据假想延拓法知函数在x=1处右导数为f’+(1)=a=f’_(1) =2再根据函数在x=1处连续,得a+b=1,解得b=-1
显然应用假想延拓法能迅速解决问题。
[1]同济大学应用数学系. 高等数学(第六版)[M]. 上海: 同济大学出版社.2007.
[2]华东师范大学数学系.数学分析(第三版)[M]. 北京:高等教育出版社. 2001.
TPO172.1
10.3969/j.issn.1001-8972.2010.14.105
谷振涛(1982-),男,山东莱芜人,山东大学在职硕士研究生,助教,主要从事研究方向:高等数学,数值分析,数学建模.

