抽样调查和区域调查法比较研究
——昆山市经济普查资料实证分析
黄正栋 江雪龙
(1江苏省苏州市统计局、2江苏省昆山市统计局/1局长、2局长,江苏苏州、昆山215004、215300)
抽样调查和区域调查法比较研究
——昆山市经济普查资料实证分析
黄正栋1江雪龙2
(1江苏省苏州市统计局、2江苏省昆山市统计局/1局长、2局长,江苏苏州、昆山215004、215300)
依照朱震葆研究员提出的“人口密度理论和区域调查方法”,对昆山市第二次经济普查资料,分别采用抽样调查和区域调查方法进行实证研究,结论是:区域调查法比抽样调查法优越。
抽样调查;区域调查;人口密度
抽样调查对于不同的调查对象需要建立不同的样本框,彼此互不兼容,为此需要投入大量的社会成本。即便如此,对于某次抽样调查,也无法了解和控制抽样标志以外调查资料的准确程度和偏差。既然如此,朱震葆研究员设想:如果能够抽取一部分社区(居委会和村委会)作为调查对象(样本框),使其与该县(市区)总体社会经济发展水平相当,来推测全县(市区)的社会经济发展水平,来替代一个个不同主题的样本框,如果能够实现,即可大大节省调查投入的人力、物力、财力和时间。我们根据其提出的“人口密度理论”和“区域调查方法”,依托第二次经济普查资料,分别采取抽样调查和区域调查方法进行测算,以检验其理论和方法的有效性和可行性。
一、昆山市各社区(居委会和村委会)人口密度和行业门类资料
人口密度理论是区域调查法的理论基础,它有一个假设:在一个国家的行政区域内,一个地区的人口密度与社会经济发展水平正相关。所以抽取的社区人口密度必须与全市(县、区)人口密度相等或者尽可能接近,这是一个约束条件。为了简便,本文将城区社区居委会和乡村村委会统一以“社区”称之。以下是全市各社区人口密度和行业门类资料。
二、建立样本框
为了比较抽样调查和区域调查,分别按照“年末从业人员”、“主营业务收入”和“人口密度”抽取样本框。
区域调查法与抽样调查法结果比较(1/4样本),是按全市300个社区的四分之一对称等距抽取,是75个社区汇总资料;抽样调查法与区域调查法比较(1/6样本),是按全市300个社区的六分之一对称等距抽取,是50个社区汇总资料(表1)。

昆山市第二次经济普查资料
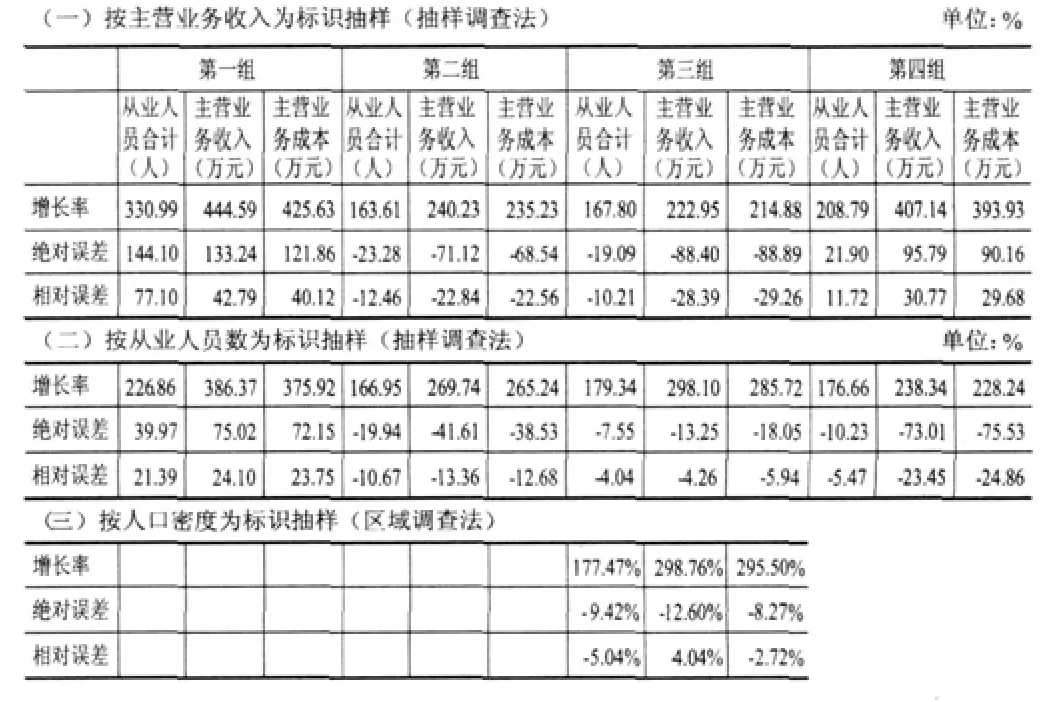
昆山市经济普查区域调查法与抽样调查法结果比较(1/4样本)
我们先看区域调查法与抽样调查法结果比较(1/4样本)表。每组都是经济普查最主要的三列数据,即“年末从业人员”、“主营业务收入”和“主营业务成本”。
第一行组是用抽样调查法,按照主营业务收入为标识排序后,按对称等距抽取后汇总的数据,可以获取四组不同的样本框,其中误差最小的是第二组(按随机原则,选中这组的机会只有25%),与第一次经济普查资料相比,主营业务收入增长率是240.23%,与全市第二次经济普查结果相比,绝对误差是-71.12%,相对误差是-22.84%。
第二行组是用抽样调查法,按照年末从业人员为标识排序后,按对称等距抽取后汇总的数据,可以获取四组不同的样本框,其中误差最小的是第三组(按随机原则,选中这组的机会只有25%),与第一次经济普查资料相比,年末从业人员增长率是179.34%,与全市第二次经济普查结果相比,绝对误差是-7.55%,相对误差是-4.04%。
第三行组是用区域调查法,按照人口密度为标识排序后,按照对称等距抽取后汇总的数据,与第一次经济普查资料相比,年末从业人员增长率是177.47%,与全市第二次经济普查结果相比绝对误差是-9.42%,相对误差是-5.04%。可以看到,比抽样调查法按照年末从业人员为标识抽取的结果误差大1个百分点。不过,主营业务收入和主营业务成本比抽样调查结果误差要小,尤其是主营业务成本,抽样调查法相对误差为-5.94%,而区域调查法为-2.72%,比抽样调查法小了一半还多。
再看,将抽样调查法二组作一下比较,分别按照主营业务收入和年末从业人员为标识,抽取的结果大相径庭,误差可以高达10倍以上。分析原因,按照年末从业人员为标识抽取的误差,要比按照主营业务收入为标识抽取的要小许多,因为主营业务收入涉及到企业的核心经济利益,而年末从业人员不涉及到企业的核心利益,而且核查起来要容易。
由于主营业务收入和主营业务成本数据准确性和可靠性比年末从业人员指标要差,所以,我们以下在作抽样调查法和区域调查法比较时,就分别以年末从业人员与人口密度为标识(表2)。

昆山市经济普查抽样调查法与区域调查法比较(1/6样本)
这张表是六分之一样本汇总资料。抽样调查法是用年末从业人员为标识按照对称等距抽取,可以获取六组不同的样本框,误差最小的是第四组(按随机原则,选中这组的机会只有16.67%)。第二次经济普查年末从业人员数与第一次经济普查比较,增长率为197.75%,与全市第二次经济普查结果相比,绝对误差为10.86%,相对误差为5.81%。
区域调查法用人口密度为标识抽取六分之一样本汇总资料,第二次经济普查年末从业人员数与第一次经济普查比较,增长率为181.03%,与全市第二次经济普查结果相比,绝对误差为-5.86%,相对误差为-3.14%。二种方法比较,区域调查法误差为抽样调查法的54%,将近一半。
需特别说明的是:抽样调查法是用年末从业人员为标识的,应该在全部调查项目中,误差是最小的。而区域调查法是用人口密度为标识的,抽取的只是与全市社会经济发展水平相当的社区样本框,不涉及到哪一个具体社会经济指标,它代表的只是社会经济发展水平与总体(全市)相一致,也就是说,人口密度是广义的社会经济指标,用它为标识抽取的社区样本框,可以为绝大多数的抽样调查提供样本框。
三、抽样估计和假设检验
区域调查法是随机抽样和有意抽样相结合的一种方法,“有意抽样有时可以得到比随机抽样更有代表性的结果”。1不过,由于我们这次按照人口密度抽取的样本框,已经包括我市全部17个门类的行业,没有对一个社区进行调整,因而是一次完全意义上的随机抽样,只是抽样标识用的是人口密度,抽样对象是社区。所以,随机抽样的误差控制理论和方法,对于我们这次区域调查法完全适用。
(一)几个重要的特征数
为了简便起见,本文只提供全市和样本(1/6样本)的人口密度计算资料。
1.均值
全市X=2363人/平方千米样本X0=2405人/平方千米
2.极值
全市:最大值=78743人/平方千米最小值=203人/平方千米
样本:最大值=78743人/平方千米最小值=203人/平方千米
3.中位数
全市=1946人/平方千米样本=1952人/平方千米
4.标准误差
全市S=149.5样本s=34.65
由此可见,用人口密度为标识抽出的样本波动比全市总体要小,稳定性要高。
5.频数
组距为5000时,全市和样本都是16个分组
全市和样本频数最大值都在200-5000组,全市=225,样本=37
组距为1000时,全市和样本都是79个分组
全市和样本频数最大值都在200-1000组,全市=107,样本=18
组距为100时,全市和样本都是786个分组
全市和样本频数最大值都在500-600组,全市=27,样本=4
由此可见,随着分组加密,频数由二项分布,转化为左偏正态分布。用人口密度为标识抽出的样本频数分布与全市总体频数分布完全一致。
(二)误差估计
我们用区间估计概率为95%时,k=1.96
1.抽样调查法对年末从业人员作区间估计
z 0-k v 3624-1.96*34.6482 3556 2.区域调查法对人口密度作区间估计 x 0-k s 2405-1.96*34.65 2337 二者比较可以看出,用人口密度作为抽样标识,其稳定性要好于以年末从业人员为抽样标识的结果。 1.代表性检验 以人口密度为标识抽取的样本框,完全遵照抽样技术对称等距随机抽取,其过程与通常抽样调查别无二致,其代表性与抽样技术抽取的样本没有任何差别。 同时,由于抽取的样本包括全市总体全部17个行业门类,从经济类型代表性上看与总体相同。 2.无偏性检验 我们用u检验样本的无偏性。我们假设样本人口密度发生显著改变。 由于1.9865小于2.576,所以假设被否定,我们认为样本与总体没有显著差异。 需要说明一下,在社会经济领域,要满足E x=X是很难得到满足的,基本上都是带有偏差的,“有时某个统计量对待估参数虽然有微小偏误,但却有其他显著优点,仍然可考虑选为估计量”2 3.稳定性检验 由于用人口密度抽取的样本,标准差s=34.65仅为总体S=149.5的九分之二。并且人口密度与其他经济指标相比,在短时间内变动要小的多。所以,我们用人口密度抽取的样本框稳定性是有保障的。 4.一致性检验 因为我们抽样过程严格遵照抽样技术的要求进行,所以根据抽样理论可知,一致性原则通常均能得到满足。 5.相关性检验 用人口密度抽取的样本,除了应该包括总体(昆山市)全部17个经济类型(门类)以外,其值分布也必需与总体相关,这样抽取的样本才真正具有经济上的代表性。为此,我们继续用年末从业人员数进行相关性检验。 经计算,得到相关系数r=0.9668>0.606(=1%)。 由此可见,用人口密度抽取的样本不仅在经济类型上与总体完全一样,而且其数值分布上也与总体高度一致,所以其经济代表性可以得到满足。 从表1看,抽样调查法以主营业务收入为标识,按照四分之一抽取样本,误差最小的第二组,主营业务收入也高达-22.84%,对于年末从业人员和主营业务成本误差也高达-12.46%和-22.56%,因此,整群抽样在此已经失效。 再看,抽样调查法如果以年末从业人员为标识,按照四分之一抽取样本,误差最小的第三组,年末从业人员误差为-4.04%,主营业务收入和主营业务成本分别为-4.26%和-5.94%。 区域调查法以人口密度为标识,按照四分之一抽取样本,年末从业人员误差为-5.04%,比抽样法大1个百分点,主营业务收入和主营业务成本误差为-4.04%和-2.72%,则要小于抽样法。 从表2看,抽样调查法以年末从业人员为标识,按照六分之一抽取样本,误差最小的第四组,年末从业人员误差为5.81%。 区域调查法以人口密度为标识,按照六分之一抽取样本,年末从业人员误差为-3.14%,比抽样法小了将近2.7个百分点。 由此可见,区域调查法即使不以具体经济统计指标(比如,这儿的“主营业务收入”和“年末从业人员”)作为标识,同样可以得到不比抽样调查法差的样本框,而且得到的是广义样本框。 抽样调查通常都是多目标调查,现行的国家统计抽样调查制度近50来个,其中调查项目最少的是“规模以下工业企业抽样调查制度”,有8项经济统计指标,即8项目标。操作过程是以“产品销售收入”作为抽样调查的标识,同时开展对全部从业人员年末数、工业总产值、成交税金、所得税、营业利润、应付工资和折旧等7项指标的调查。由于至今数学理论上没有解决在以一个目标作为标识时,同时保证其他调查项目的代表性问题。因而,在用这些非标识指标推算总体时,它们的代表性、准确性、可靠性和可信性都出了问题!所以,抽样技术在实际应用中,遇到多目标调查时,只对作为标识的主要社会经济统计指标有代表性,也就是说,目前正在贯彻执行的国家统计抽样调查制度在理论上存上缺陷。 而区域调查法只以一个“人口密度”社会指标作为标识,对社区(居委会和村委会)进行整群抽样(我们这次是等群抽样),是名副其实的单目标抽样,从而绕过了多目标“代表性泥淖”。 在当前社会经济发展极其迅速的今天,尤其是对于像我国这样的发展中大国,社会日新月异,经济超常发展,还没有等普查资料整理出来(我国一项大规模普查,资料的整理到发布最少需要一年以上,国外需要2-3年以上),社会经济状况已经面目全非,许许多多企业已经消失得无影无踪,但是它们还存在在我们的样本框里。即使是直接管理它们的工商局和税务局,到年末也无法统一它们的企业统计数字。因此,一年前抽样调查建立起来的样本框的可靠性存在问题。 相比在非不可知因素(比如,战争、大规模灾变、大规模疾病流行等)不存在的情况下,人口出生率、人口死亡率和人口流动性在一段时间内比较稳定,从而保证了区域内人口密度的稳定,只要我们行政区划发生变更时,能够及时调整,统计口径上不会产生任何问题。所以,应用人口密度抽取的样本框,通常只需要逢到人口普查和人口抽样调查的年份,每5年作一次性重新抽样即可。 由此可见,人口密度抽取的样本框稳定性,显然要高于用经济指标作为标识抽取的样本框。 区域调查法是以社区(城镇居委会和农村村委会合称)为抽样对象的整群抽样。通常以县(县级市和城区)为总体,抽样单位为社区,样本量,按照昆山市的经验,占一个县的六分之一左右适宜,各地也可以根据情况设八分之一或者十二分之一。社区无论是居委会还是村委会通常都设会计一名,会计同时兼统计业务。市县统计局只需要对这些会计作一些业务培训,提高他们的荣誉感、使命感、责任心和业务能力,就可以为我们提供很好的服务。由于区域调查法抽中的社区,通常5年才会变更一次,这些会计绝大多数会成为业务熟练的优秀调查员。就我们统计部门来说,不需要再为每项抽样调查配置调查员了。 根据昆山市这次实例,区域调查法实际上是二阶段过程。 第一阶段,抽取以社区为调查单位的样本框。这一阶段只需要社区人口和面积二项指标,计算出人口密度。为了使抽中的社区包括全市全部经济门类,以增加样本的代表性,在收集社区人口密度的同时,提供社区的经济门类资料,这次经济普查已经包括这些资料,这些社区样本框,每5年调整一次。 第二阶段,就是根据每次抽样调查的项目,由社区提供相应的资料。比如,如果我们需要规模以下服务业的资料,就由这些社区提供相应的规模以下服务业资料,根据这些社区占全市的比重(以这次经济普查为基年)和增长率,就可以推算出全市总体的数据了。非特殊原因,基年资料每5年调整一次。 区域调查法以县(市区)为总体、以社区(居委会和村委会)为抽样对象的,不需要经过街道和乡镇一级的直报制度,由此可以减少外界的干预。 (责任编辑:倪进) 10.3969/j.issn.1674-8905.2010.05.021 1《统计大辞典》.郑家亨主编,中国统计出版社,1995年3月版P 192。 2《实用推断统计方法》.周铭主编,宁夏人民出版社,P 71。(三)几项重要的检验
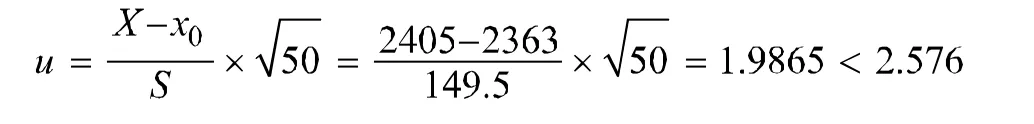
四、几点结论
1.区域调查法可以得到广义样本框
2.区域调查法不受多目标代表性问题困扰
3.区域调查法样本框稳定
4.区域调查法是经济廉价的调查方法
5.区域调查法是简便易行的调查方法
6.区域调查法是抗干扰的调查方法

