凹陷立管的极限强度和疲劳寿命分析
余 折, 王德禹
(上海交通大学,上海200242)
凹陷立管的极限强度和疲劳寿命分析
余 折, 王德禹
(上海交通大学,上海200242)
用MSC.Patran建立三维模型,然后用ABAQUS计算立管的极限强度,用MSC.Fatigue进行全寿命分析。计算与分析结果表明:最大凹陷深度的增加使立管的极限强度和疲劳寿命减少;凹陷区域长度的变化对立管极限强度的影响不大,对疲劳寿命的影响较大;增加立管管壁厚度会提高立管的极限强度,但管壁越厚,凹陷损伤对立管极限强度的影响越大;立管在轴向拉伸力和纵向弯矩共同作用下,只要轴向拉伸力在合适的范围内,凹陷对立管极限强度的影响非常小。
立管;凹陷;极限强度;疲劳寿命;ABAQUS;MSC.Fatigue
0 引言
海洋立管在使用过程中,难免会受到某些物体的冲撞或其他非正常载荷的作用而产生凹陷。这些凹陷的存在,会影响立管的强度,对立管的安全运行产生隐患。限于财力、物力、人力,不可能也没有必要对所有凹陷的立管进行更换或返修,因此研究凹陷立管的极限强度和疲劳寿命是世界各国普遍关注和迫切需要解决的重要课题。
目前对损伤圆管构件剩余强度方面的研究,采用的方法主要有[2]:①简化模型的理论分析方法;②实验方法;③有限元方法。而有限元方法作为一种非常有效的方法,近年来被广泛采用。Claudio Ruggieri[3]等用有限元方法结合实验方法分析侧向载荷对凹陷立管的影响,发现立管在局部凹陷和整体弯曲变形耦合作用下,能极大地降低塑性极限载荷,而凹陷区域的增加会对立管的承载能力造成极大的影响。Karamanos[4]等通过非线性有限元模型和解析模型,研究外压对管的极限侧向载荷和吸收能量的能力的影响,发现当外压较低时,会使管的极限承载能力和吸收能量的能力显著下降;Brooker[5]用有限元方法对两端约束的管进行准静态侧向凹坑响应分析,研究管壁厚度、直径、长度以及屈服应力水平等参数的影响;Spyros A.Karamanos[6]等利用有限元模型和解析模型,研究了有内压存在的、受侧向准静态载荷的、楔形凹坑的管构件的结构响应。本文采用有限元方法,对轴向拉伸力和弯矩单独或共同作用下的有凹陷的立管进行强度分析,研究凹陷深度、凹陷影响区域的长度、管壁厚度等参数对立管极限强度的影响。目前对于立管的疲劳寿命的分析,主要有实验方法、有限元方法和解析方法这3种方法,本文使用MSCFatigue软件对有凹陷的立管进行全寿命分析,研究凹陷深度以及凹陷影响区域的长度对立管的疲劳寿命的影响。

图1 受损立管的凹陷模型

图2 有凹陷立管的有限元模型
1 模型介绍
本文利用ABAQUS研究有局部凹陷损伤的立管的极限强度,模型假设:①材料为各项同性和理想弹塑性;②不考虑残余应力对极限强度的影响;③凹陷的几何形状如图1所示。设Ld为凹陷区域的长度,do为凹陷中心处的深度。假设凹陷形状关于平面1-2和平面2-3对称,凹陷深度在凹陷区域内呈线性变化,任意位置处的凹陷深度dw=d0(1-z/Ld),其中z为沿圆管轴向的坐标位置,坐标原点为凹陷中心。建模时取管的1/4模型建模,采用四边形壳单元S4建模,在凹陷区域用三角形或四边形的单元进行细化。有限元模型如图2所示。为模拟对称条件,把位于2-3平面和在Z=0处的1-2平面上的节点用对称条件约束住,对管端部采用平面假定,使其能轴向自由滑动和两端面自由转动,故对Z=L处的1-2平面上的节点约束其1,2方向的位移。模型长度取1 m,材料钢的弹性模量E=206.82 MPa,泊松比v=0.3,钢的屈服极限是413.64 MPa。立管的外径是219.08 mm(8.625 in),厚度是15.06 mm(0.593 in)。
2 有凹陷的立管在组合外载荷作用下的包络线
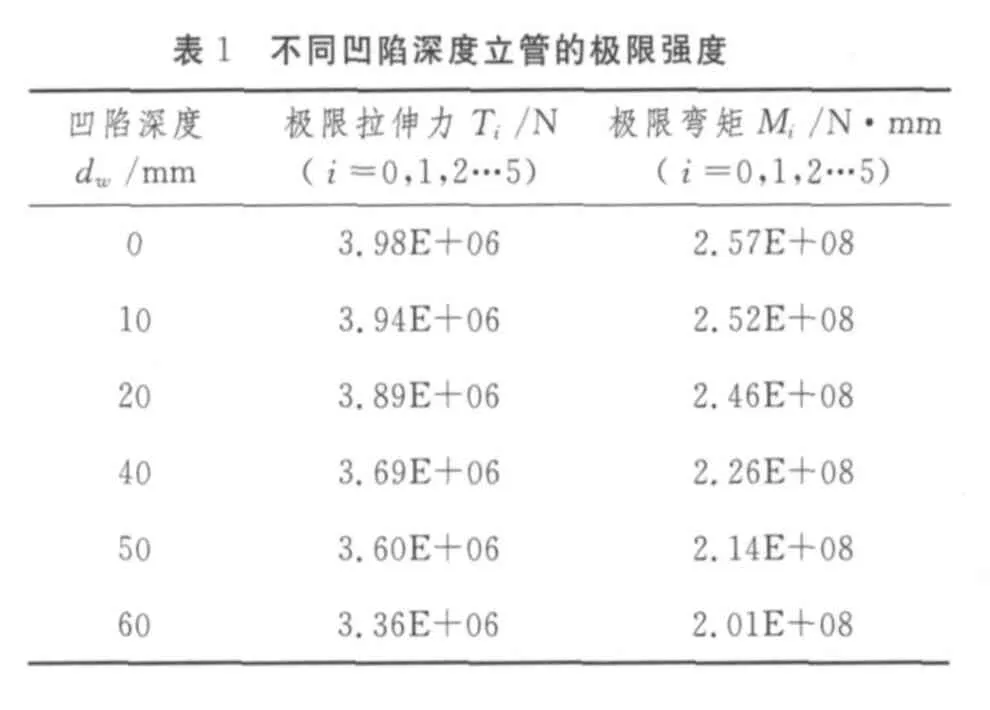
对凹陷区域长度Ld=250 mm的立管,取不同的最大凹陷深度dw=0,10 mm,20 mm,40 mm,50 mm,60 mm,施加如图1所示的轴向拉伸力或弯矩,计算立管轴向拉力或纵向弯矩单独作用下的极限拉伸力和极限弯矩值,计算结果如表1所示。其中,Ti,Mi(i=0,1,2…5)分别对应最大凹陷深度为0,10 mm,20 mm,40 mm,50 mm,60 mm的立管极限拉伸力和极限弯矩值。再确定这些立管在纵向弯矩和轴向拉伸力共同作用下的极限拉伸力-弯矩包络线,绘制出的极限拉伸力-弯矩包络线如图3~图7所示,每条曲线包括11个点,分别对应于有10,20,30,40,50,60,70,80,90%Ti(i=0,1,2…5)的初始轴向拉力作用的极限弯矩值,及弯矩或拉伸力单独作用时的极限值。
?


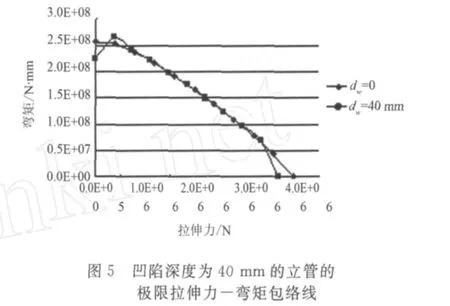
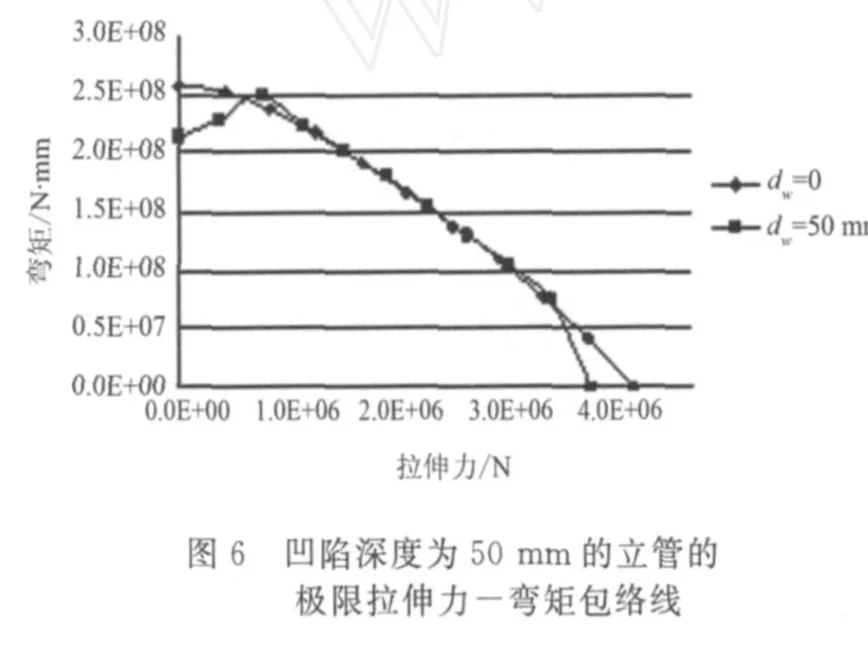
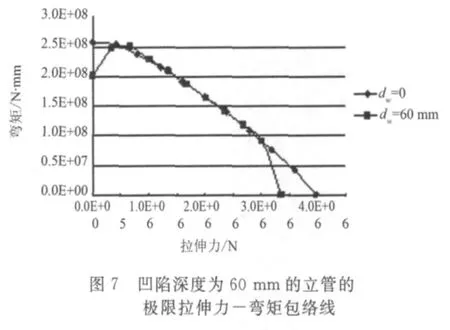
从图中可以看出,对于没有凹陷的,即最大凹陷深度dw=0的立管,立管的极限弯矩值随着初始轴向拉伸力的增大而减小。而对于所有有凹陷的立管,当拉力初始增加时,立管的极限弯矩值增大,而当拉力继续增加时,立管的极限弯矩值却随之减小。上述现象可能是轴向拉力能在立管凹陷区域附近形成膜张力,导致管壁局部刚度加强,所以在一定范围内,轴向拉力越大,极限弯矩值越大;继续增大轴向拉力时,轴向拉力使立管的应力应变值加大,导致立管的极限弯矩值减小。从图中还可以看到,对于不同凹陷深度的立管,初始轴向力在某个范围内时,立管的极限弯矩值与同等轴向拉力的作用下的无凹陷立管的极限弯矩值相接近,并且随着凹陷深度增大,这个范围逐渐减小。具体而言,当凹陷深度分别为dw=10 mm,20 mm,40 mm,50 mm,60 mm,立管的初始轴向拉力分别在0.1 T1~0.9 T1,0.2 T2~0.9 T2,0.2 T3~0.9 T3,0.3 T4~0.8 T4,0.3 T5~0.8 T5的范围内时,立管的极限弯矩值与同等轴向拉力的作用下的无凹陷立管的极限弯矩值非常接近。上述现象表明对于有凹陷的立管,顶部张力在一定范围内作用时,能提高立管的极限弯曲强度,顶部张力的存在对于提高有凹陷立管的极限弯曲强度是十分有利的。
3 不同的凹陷损伤对立管的极限拉伸力和极限弯矩的影响
3.1 不同最大凹陷深度对极限拉伸力和极限弯矩的影响
对凹陷区域长度Ld=250 mm的立管,前面计算过最大凹陷深度分别为0,10 mm,20 mm,40 mm,50 mm,60 mm的立管,在轴向拉力或弯矩单独作用下的极限拉伸力Ti和极限弯矩值Mi(i=0,1,2…5)。把计算结果整理绘制成曲线,如图8所示。显然,随着凹陷深度加大,极限拉伸力或极限弯矩减小,而且最大凹陷深度的损伤对极限弯矩的影响比对极限拉伸力影响大。
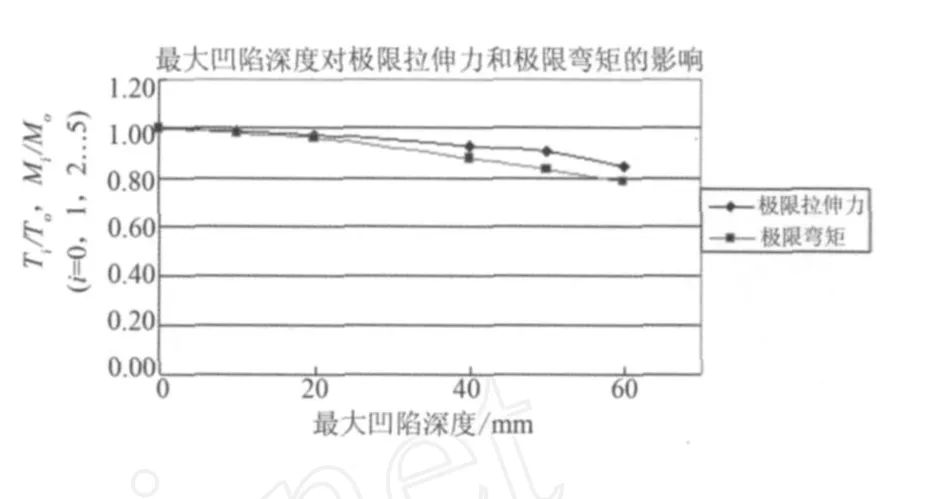
图8 最大凹陷深度对极限拉伸力和极限弯矩的影响
3.2 损伤区域长度对极限拉伸力和极限弯矩的影响
对有一定凹陷深度的立管(dw=10 mm或40 mm),取不同的损伤区域长度Ld=50 mm,100 mm,150 mm,200 mm,250 mm,350 mm,450 mm,计算其在拉力或弯矩单独作用下的极限拉伸力或极限弯矩。计算结果如图9、图10所示。从图9中可以看出,对凹陷深度为10 mm的立管,增加损伤区域长度对其极限拉伸力几无影响,对于凹陷深度为40 mm的立管,当Ld<100 mm时,增大损伤区域长度,极限拉伸力和极限弯矩都增加,当Ld>100 mm时,再增加损伤区域长度,极限拉伸力只稍稍增大。可知一定深度下,凹陷区域的长度对极限拉伸力的影响不大,但是凹口坡度的斜率(dw/Ld)对极限拉伸力有影响,特别当dw/Ld>0.4时,dw/Ld的增大会降低立管的极限拉伸力。从图10中,可以看出凹陷深度为10 mm的立管,增加损伤区域长度会稍稍减小其极限弯矩,这是因为增加凹陷区域长度,会减小立管的剖面模数,从而降低立管的极限弯矩;对于凹陷深度为40 mm的立管,当Ld>100 mm时,随着损伤区域长度的增加,其极限弯矩稍稍减小,但当Ld<100 mm时,随着凹陷区域长度的减小,极限弯矩反而增大,可知当凹陷坡度较大时(dw/Ld>0.4),dw/Ld的增大会降低立管的极限弯矩。总的来说,损伤区域长度对立管的极限拉伸力和极限弯矩的影响都不大;凹口坡度的斜率(dw/Ld)较大时,dw/Ld的增加会降低立管的极限拉伸力和极限弯矩。
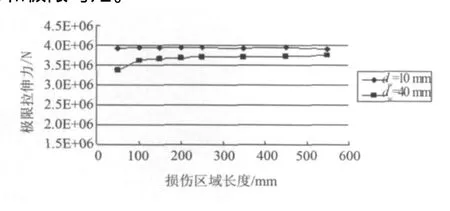
图9 凹陷区域长度对极限拉伸力的影响

图10 凹陷区域长度对极限弯矩的影响
3.3 不同的立管壁厚t的影响
假定钢管的外径219.08 mm不变,损伤影响区域的长度Ld为250 mm,改变立管的壁厚t,计算其在不同凹陷深度dw的极限拉伸力和极限弯矩,计算结果如图11、图12所示。t越大,立管的截面积越大,相应的极限拉伸力和极限弯矩越大。在t较小的情况下,损伤对极限拉伸力和极限弯矩的影响并不大,但随着t的增大,损伤的影响加大;对比图11、图12,可以看出同样的立管,损伤对于极限弯矩的影响比对极限拉伸力的影响大。

图11 立管壁厚对极限拉伸力的影响
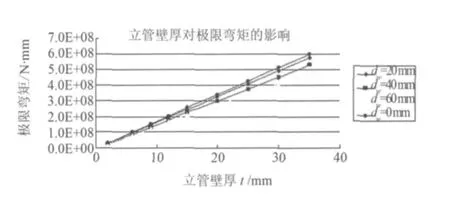
图12 立管壁厚对极限弯矩的影响
4 凹陷损伤对立管疲劳寿命的影响
从前面的分析可知,当立管有凹陷时,对极限强度会有较大的影响,下面分析凹陷对立管的疲劳寿命的影响。取长度为2 m的立管,两端简支,在立管的两端施加幅值为M恒幅的交变弯矩[7],交变弯矩的载荷形式如图13所示。立管的外径为219.08 mm,厚度为15.06 mm,凹陷影响区域的长度为500 mm,取幅值M=0.35M 6,其中M6为最大凹陷深度60 mm的立管在纯弯矩作用下的极限弯矩,有限元模型如图14所示。本文用MSC.Fatigue软件对立管进行全寿命分析,施加的交变载荷随时间周期变化的形式如图所示。取材料为FeE52D,材料的弹性模量E=200 MPa,泊松比v=0.3,屈服极限为425 MPa,极限拉伸强度为550 MPa,其S-N曲线如图15所示。
4.1 不同的最大凹陷深度对立管疲劳寿命的影响
取立管的凹陷影响区域的长度Ld=500 mm,最大凹陷深度分别10 mm,20 mm,40 mm,50 mm,60 mm时,计算立管的疲劳寿命,结果如表2所示。从表中可以看出,当凹陷深度较小(dw=10 mm,20 mm)时,立管的载荷循环次数超过1E7次。一般认为,材料或构件能承受N>1E7而不至断裂的最大对称交变应力幅值为材料或构件的疲劳极限。若应力幅值高于或等于疲劳极限时的寿命为无限寿命,则对于凹陷深度较小的管,在该载荷下其疲劳寿命是无限的。随着最大凹陷深度的加大,外载荷的循环次数明显减少,立管的疲劳寿命也会相应减少。总的说来,当立管凹陷影响区域的长度相同时,最大凹陷深度的加大会减少其疲劳寿命。有凹陷损伤的立管的外载荷循环次数的对数分布图如图16所示,从图中可以看出在凹陷附近的材料是最容易发生疲劳损坏,这是由于在凹陷处会产生应力集中,从而使疲劳强度降低。

表2 不同最大凹陷深度立管的疲劳寿命




4.2 不同的凹陷区域长度对立管疲劳寿命的影响
对有一定凹陷深度的立管(dw=40 mm或60 mm),取不同的损伤区域长度Ld=50 mm,100 mm,150 mm,200 mm,250 mm,350 mm,450 mm,550 mm计算其疲劳寿命,计算结果如表3、表4所示。从计算结果中可知,对于同一深度下的立管,损伤影响区域越大,疲劳寿命越大,不过当影响区域长度足够长时,外载荷的循环次数>1E7,认为立管在该载荷下不会发生疲劳损坏。由表中数据可知,当Ld很小时,立管都是低周疲劳,计算出来的疲劳寿命并不可靠,但是也可反映出一定深度下,损伤立管的疲劳寿命随着损伤区域长度的增加而明显减少这一规律。这是因为,当影响区域长度较短时,凹陷坡度的斜率dw/Ld较大,这样在凹陷附近会产生很大的应力集中,使得该区域很容易发生疲劳损坏,降低立管的疲劳极限。
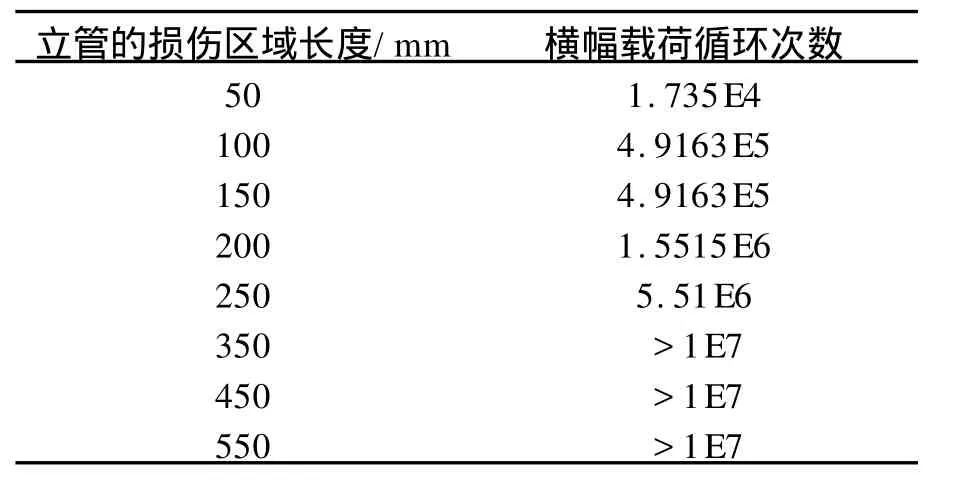
表3 dw=40 mm时,不同损伤区域长度对其疲劳寿命的影响
5 总结
(1)本文采用有限元方法分析了不同凹陷深度的立管在弯矩和拉伸力共同作用,以及它们单独作用下的极限强度,并绘制出极限拉伸力-弯矩包络线。计算结果表明:立管在端部拉伸力或弯矩单独作用下,凹陷损伤会明显降低立管的极限拉伸力或极限弯矩;但在拉伸力和弯矩共同作用下,只要拉伸力在合适的范围内,凹陷损伤对立管极限强度的影响是非常小的。由此可见,有顶部拉伸力的立管,有利于减小凹陷带来的危害。
(2)分析最大凹陷深度、凹陷区域的长度和管壁厚度等参数对立管拉伸力或极限弯矩的影响。结果表明:最大凹陷区域越深,立管在拉伸力或弯矩单独作用下的极限拉伸力或极限弯矩值越小。一定深度下,损伤区域长度的变化对立管的极限强度影响非常小。凹陷深度、凹陷区域长度和管外径一定时,管壁厚度的减少会降低立管的极限拉伸力或极限弯矩;管壁越厚,凹陷对立管的极限弯矩或极限拉伸力的影响越大。
(3)分析不同凹陷深度的立管在交变的恒幅载荷作用下的疲劳寿命,结果表明,随着凹陷深度的加大,立管的疲劳寿命减小。
(4)对同一深度下,不同凹陷影响区域长度的立管进行疲劳寿命分析,发现随着凹陷影响区域长度的增加,疲劳寿命增加,当长度足够长时,凹陷影响区域的长度再增加,也不会影响立管的疲劳寿命。
[1] 陈铁云,邵文蛟,周义先.损伤圆柱壳的可靠性分析[J].交通部上海运输科学研究所学报,1988,2:12-22.
[2] 邵炎林,何炎平.海洋结构物中典型圆管构件的碰撞损伤研究[J].中国海洋平台,2006,21(1):35-40.
[3] Claudio Ruggieri,Jose A lfredo Ferrari,Jr.Structural.behavior of dented tubular members under lateral loads[J].Offsho re Mech.Arct.Eng,2004,126:191-197.
[4] Karamanos SA,Eleftheriadis C.Collapse of pressurized elastoplastic tubular members under lateral loads[J].International Journal of Mechanical Sciences,2004,46(1):35-56.
[5] Brooker D C.Anumerical study on the lateral indentation of continuously suppo rted tubes[J].Journal of Constructional Steel Research,2004,60:1177-1192.
[6] Spyros A,Karamanos,Kyros P.Andreadakis.Denting of internally pressurized tubes under lateral loads[J].International Journal of Mechanical Sciences,2006,48:1080-1094.
[7] Netto T A,Lourenco MI,Botto A.Fatigue perfo rmance of pre-strained pipesw ith girth weld defects:Full-scale experiments and analyses[J].International Journal of Fatigue,2008,30:767-778.
Analysis of Ultimate Strength and Fatigue Life of the Dented Riser
YU Zhe, WANGDe-yu
(Shanghai Jiao Tong University,Shanghai 200242,China)
To study the ultimate strength and fatigue life of the dented riser,MSC.Patran is used to build 3D model.The ultimate strength and life cycle of risers are analyzed by ABAQUS and MSC.Fatigue.The results show that:the ultimate strength and fatigue life significantly reduced as themaxim um dep th of dent increase.The change of the length of dented region had little effect on ultimate strength,but greater influence on the fatigue life.To increase the thickness of the riser will greatly imp rove the ultimate strength,but the thicker of the wall,the greater influence on the ultimate strength of the dented riser.As long as the axial tensile fo rce within asuitable region,the influence of the dent on the ultimate strength of the riser under com bined axial tensile fo rce and longitudinal bending moment is very small.
riser;dent;ultimate strength;fatigue life;ABAQUS;MSC.Fatigue
P756.2
A
1001-4500(2010)03-0030-06
2010-01-11
海洋工程国家重点实验室自主研究课题(GKZD010006)和国家科技重大专项(2008ZX05026-05)资助
余 折(1983-),女,硕士研究生,主要从事海洋立管的研究。

