计算单位球上Henon方程正解的分歧方法

李昭祥,杨忠华,朱海龙

计算单位球上Henon方程正解的分歧方法

李昭祥1＊,杨忠华2,朱海龙3

(1.上海师范大学计算数学系,上海200234;2.上海师范大学科学计算上海高校重点实验室,上海200234; 3.安徽财经大学统计与应用数学学院,安徽蚌埠233030)

首先应用分歧方法计算单位球上Henon方程边值问题O(3)对称正解,然后以Henon方程中的参数l为分歧参数,在O(3)对称正解解枝上用扩张系统方法求出对称破缺分歧点,进而用解枝转接方法计算出具有其它对称性质的正解.

Henon方程;对称破缺分歧;扩张系统;解枝转接

0 引言

本文主要讨论单位球上Henon方程边值问题

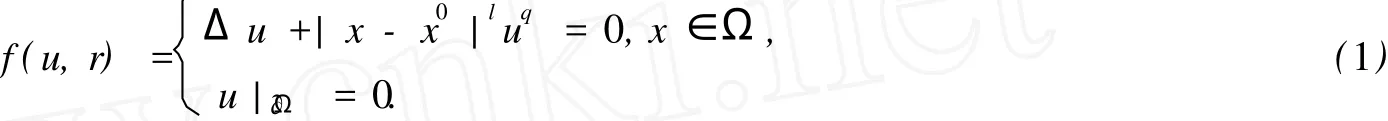
正解的计算,这里Δ是Laplace算子,x=(x1,x2,x3),Ω是空间中的单位球,l≥0,x0=(0,0,0),∂Ω是Ω的边界.q≥1在天体物理中称为多方指数.Henon[1]在研究旋转星系结构的稳定性时提出了方程(1),而Henon方程(1)的解的各种性质至今已被许多作者所研究[2-6].

大量出现在物理、天文、力学领域中的非线性椭圆型方程边值问题(1)解的存在性和多解性研究,近年来逐步成为偏微分方程研究的一个重要领域.一开始的工具是有序Banach空间中的上下解方法[7,8],后来主要是临界点理论[9,10].临界点理论中的山路引理和极大极小定理被用来证明非线性椭圆型方程边值问题解的存在性和多解性.为了进一步了解这些解的结构和形状,如何在数值上具体计算出这些多解就很自然地摆在人们面前了.目前,国内外先后出现了5种计算该类问题的数值方法:单调迭代格式(M IS)[11,12]、山路算法(MPA)[13]、高环绕算法(HLA)[14]、极大极小算法(MNA)[15,16]和搜索延拓法(SEM)[17].M IS基于有序,Banach空间中的单调迭代方法.MPA,MMA和HLA主要基于临界点理论中的山路引理和极大极小定理的数值实现.山路算法由Choi-McKenna提出,一般的此算法只能找到Morse指标为0或1的解.当f(u,r)关于u是奇函数时,MPA通过区域的对称性也可找到某些变号解.高环绕算法由Ding,Costa,Chen所建立,可以得到某些变号解.极小极大算法是Li和Zhou为寻找一般Morse指标的临界点而设计的一种算法.他们的算法在数值计算上更具构造性,并能计算某些高Morse指标的解.搜索延拓法和有限元法迭代完成计算.分歧方法已经被作者成功应用在求解单位正方形上Henon方程的边值问题上[18].分歧方法的优点是它能够尽可能多地把具有任意Morse指标和不同对称性的解计算出来,而且能够利用对称性简化计算,另外它能够有效地解决其它方法中存在的迭代初值选取困难的问题.

通过引进分歧参数λ,把(1)嵌入到如下的分歧问题:

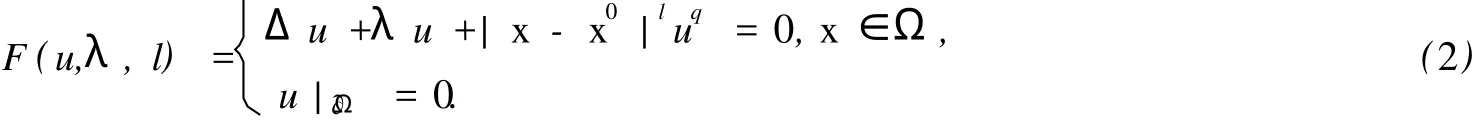
根据分歧理论[19,20],分歧问题(2)从它的分歧点出发可沿着问题(2)的非平凡解枝延拓到λ=0,可以求出问题(1)的非平凡解,其中有物理学家感兴趣的正解.

利用极坐标变换,问题(2)可化为

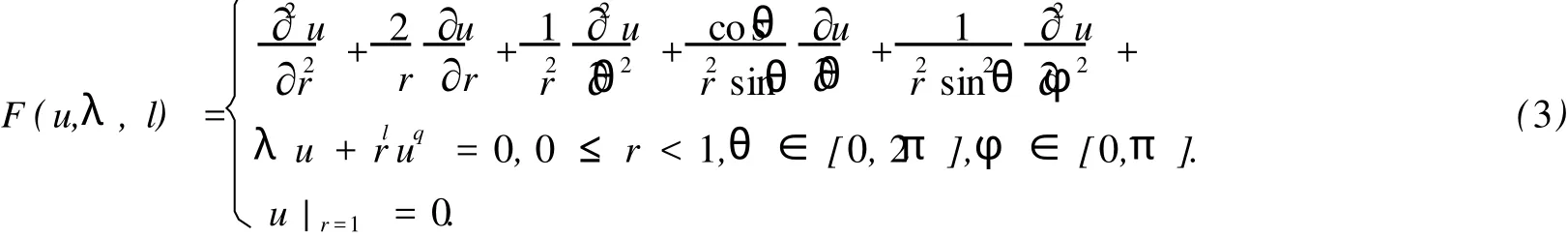
本文在第1节首先应用分歧方法计算Henon方程边值问题(1)的O(3)对称正解,然后在第2节,由对称破缺分歧理论,把Henon方程中的参数l作为分歧参数,在O(3)对称正解解枝上用扩张系统方法求出对称破缺分歧点,用解枝转接方法计算具有其它对称性质的正解,最后给出了数值结果.

1 O(3)对称正解的计算

1.1 方程O(3)的等变性

∀λ∈R,问题(3)是Γ等变的,这里Γ=O(3)×Z2,Z2=(I,-I),即满足

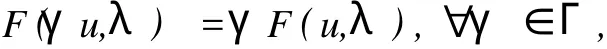
这里

∀λ∈R,u≡0是问题(3)的Γ对称平凡解.我们首先考虑问题(3)的O(3)对称的非平凡解,此时解u (r,θ,φ)与θ,φ无关,它们满足如下的二点边值问题:

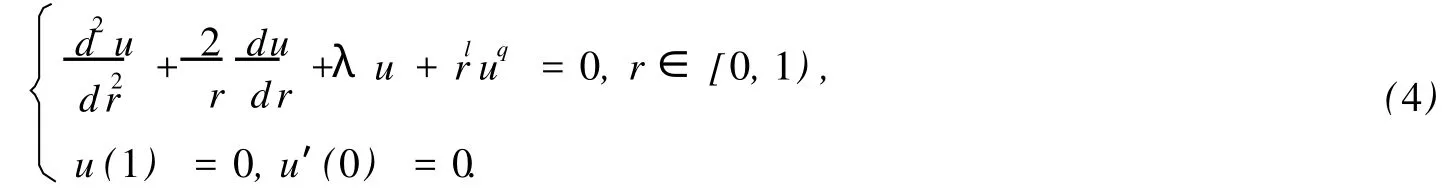
当λ从分歧点出发沿着(4)的非平凡解延拓到λ=0时,就可以得到问题(1)的O(3)对称解,即满足:

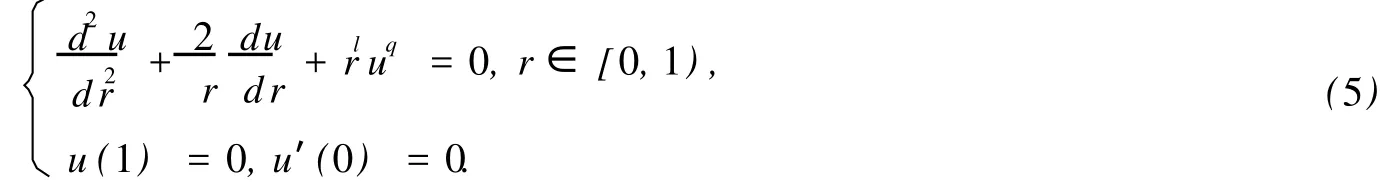
边值问题(4)关于平凡解u≡0的线性化问题为:

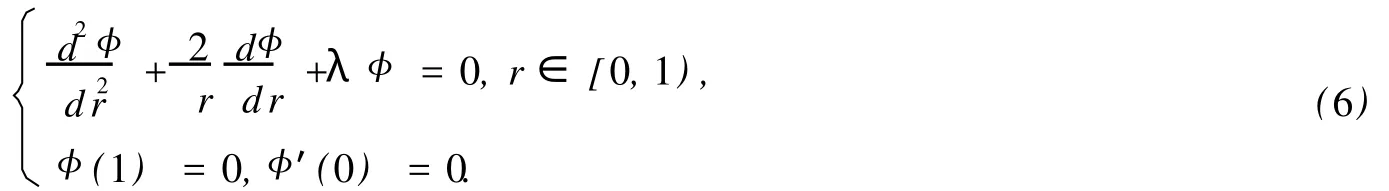
1.2 数值方法

算法:

第一步:将[0,1]N等分,用二阶中心差分来离散化问题(6).

求得其特征值以及对应的特征函数,我们取第一个特征值λ1及其对应的特征函数e.

第二步:令u=τe+w,μ=λ-λ1,τ是小参数,代入式(5),用中心差分离散后得其离散化形式为(取q= 3)

将τ延拓到足够大,例如τ=0.1,可以得到远离平凡解的u和λ.

第三步:用上述方法得到u和λ作为初始出发点,以λ为参数,直接求解方程(4)的离散化形式,将λ延拓到0,就得到了边值问题(5)的正解.以圆的半径为轴,旋转一周就得问题(1)的O(3)对称正解在大圆上的表示.

1.3 数值结果

用本文算法成功地计算出了边值问题(1)的O(3)对称正解,图1给出l=0;1;5;10时问题(1)的O(3)对称正解.

图1 q=3,l=0;1;5;10时,问题(1)的O(3)对称正解在大圆上的表示Fig.1 TheO(3)symmetric positive solutions to problem(1)forq=3,l=0;1;5;10 on the great circle

2 其他对称正解的计算

2.1 O(3)对称正解的对称破缺

考虑问题(3)的与φ无关的解,即它们在(r,θ)平面上满足下列O(2)×Z2等变问题:

将区间[0,1]N等分,区间[0,2π]M等分,本文取N=50,M=100,用中心差分来离散上述问题可得

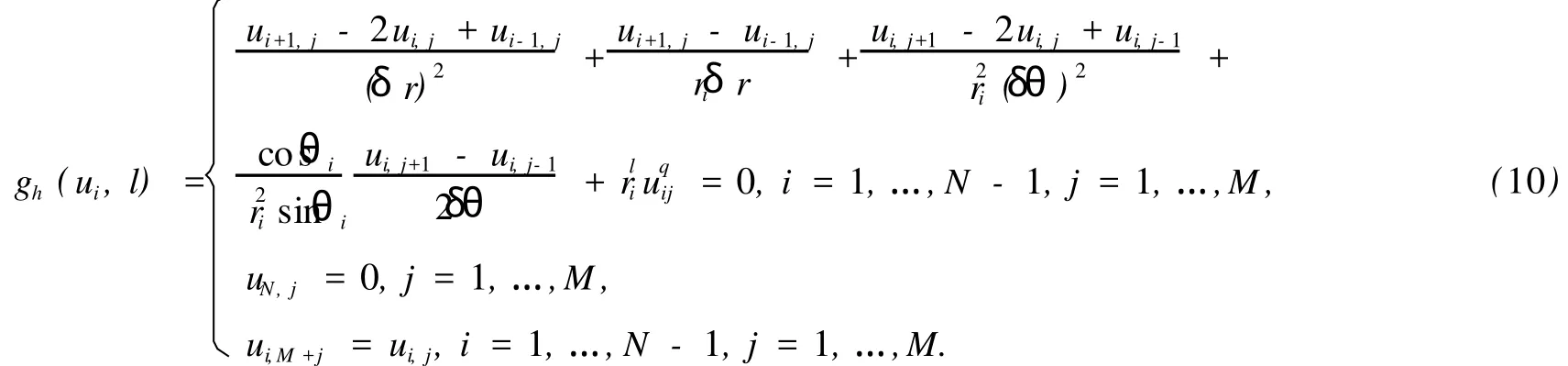
这里

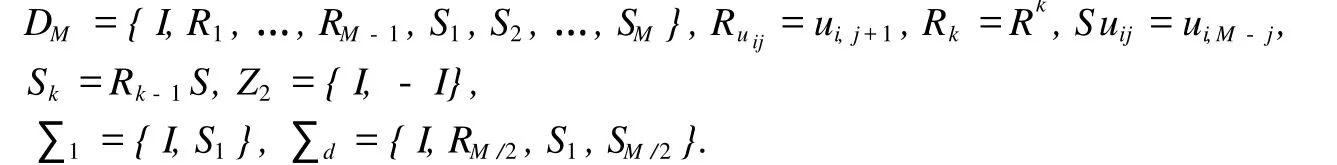
将l作为延拓参数,从l=0时问题(9)的O(2)对称正解(即问题(1)的O(3)对称正解)出发,用延拓方法同样可得问题(1)的O(3)对称的正解(如图1).

在延拓的同时,通过监视相应的Jacobi矩阵Fu(u,l)的特征值,发现在l=0.167、2.704、5.266、7.857附近出现特征值符号改变,而相应的特征向量在(r,θ)平面上分别具有∑1、∑d、D3、D4对称性,这是潜在的对称破缺分歧点[19,20],其对称性由相应的零特征向量的对称性决定.

2.2 对称正解枝上对称破缺分歧点的计算

以下令∑为一个迷向子群,X∑为∑的不变子空间,由于

可进行如下空间分解X∑=XO(3)⊕W,这里W=X∑∩(XO(3))⊥,(XO(3))⊥是XO(3)的正交补空间.

引理1 如果u∈XO(3),那么∀l∈R,下列结论成立

(i)g(u,l),g(u,l)∈XO(3),

(ii)XO(3)和W是gu(u,l)和gul(u,l)的不变子空间,

(iii)若v∈XO(3),那么XO(3)和W是guu(u,l)v的不变子空间.

证明 (i)由等变性(11)可知,若u∈XO(3),那么这就意味着g(u,l),gl(u,l)∈XO(3).

(ii)

(1)由式(11)可知

若u,v∈XO(3),那么

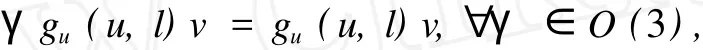
于是gu(u,l)v∈XO(3),也就是说XO(3)是gu(u,l)的不变子空间.类似地可以证明XO(3)也是gul(u,l)的不变子空间,X∑是gu(u,l)和gul(u,l)的不变子空间.

(2)另外由式(12)可知

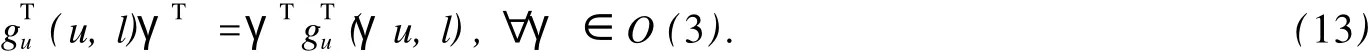
若v∈XO(3),那么

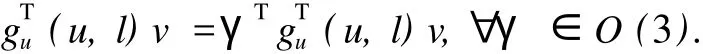
于是gTu(u,l)v∈XO(3),即XO(3)是gTu(u,l)的不变子空间.类似地XO(3)也是gTul(u,l)的不变子空间,X∑是gTu(u,l)和gTul(u,l)的不变子空间.

(3)若v∈XO(3),那么gTu(u,l)v∈XO(3),于是

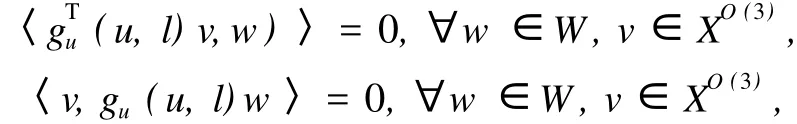
由此可知gu(u,l)w∈W,即W是gu(l)的不变子空间.类似地,W是gul(u,l)的不变子空间.

(iii)由式(11)可知

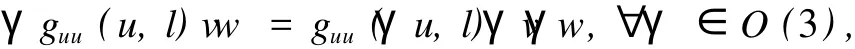
若u,v,w∈XO(3),那么

这意味着guu(u,l)vw∈XO(3),即XO(3)是guu(u,l)v的不变子空间,类似地X∑也是guu(u,l)v的不变子空间.

由式(11)推出

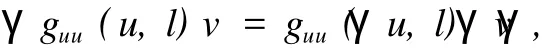
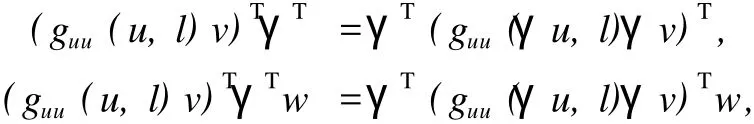
于是若u,v,w∈XO(3),那么(guu(u,l)v)Tw∈XO(3),也就是说XO(3)是(guu(u,l)v)T的不变子空间.当w∈W,v,h∈XO(3)时

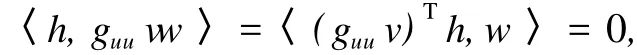
这就是说guuvw∈W,于是W是guuv的不变子空间.

在O(3)对称正解枝上碰到奇异点(u0,l0),此时g0u=gu(u0,l0)奇异且N(g0u)=span{φ0},R(g0u)={x∈X∑〈|ψ0,x〉=0},这里φ0∈W,ψ0∈W分别是g0u和(g0u)T的零特征向量,由引理1推出〈ψ0,gl(u0,l0)〉=0.令vl∈XO(3)是

的唯一解.如果满足

此时称(u0,l0)为(9)关于l的O(3)-∑对称破缺分歧点.

下面是计算O(3)-∑对称破缺分歧点的扩张系统:

其中y=(u,φ,l)∈Y=XO(3)×W×R,y0=(u0,φ0,l0),h0是使φ规范化的一个泛函,在具体计算时,取〈h0, φ〉=φi,φi是φ离散后的第i个分量.

定理1 扩张系统(16)在O(3)-∑对称破缺分歧点y0处是正则的.

证明 显然

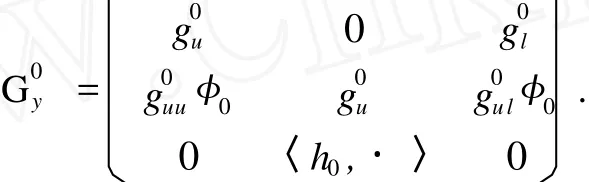
先证明G0y:Y→Y是一一的,即由

推出Z=(v,w,α)T=0,这里v∈XO(3),w∈W,α∈R.展开(17)可得:

由(18)式推出v=αvl,代入式(19)可得α〈ψ0,(g0uuv1φ0+g0ulφ0)〉=0,于是由式(15)可推出α=0,从而v=0,再由g0uw=0,〈h0,w〉=0可推出w=0.类似地可以证明G0y:Y→Y是到上的,从而得到G0y的正则性.

由于G0y是正则的,故可以用Newton方法求解扩张系统(16),在监视O(3)对称正解枝的Jacobi矩阵gu(u,l)时,特征值接近于0时的u＊∈XO(3)和l＊∈R和相应的特征向量φ＊∈W可取为Newton迭代的初始猜测.下面是计算结果(表1).

表1 对称破缺分歧点Table 1 The symmetry-breaking bifurcation points

2.3 ∑对称解枝的转接

令O(3)-∑对称破缺分歧点为l=l0,u=u0∈XO(3),ψ0∈W,φ0∈W,计算表明

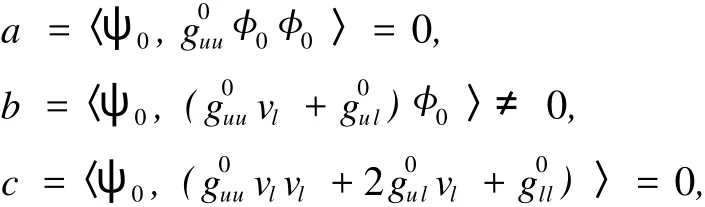
这里vl∈XO(3)是(14)的唯一解.于是式(15)是成立的.由代数分歧方程[19,20]可知,在对称破缺分歧点处,沿着O(3)对称解枝的切向为(vl,1),沿着∑对称解枝的切向为(φ0,0).定义:

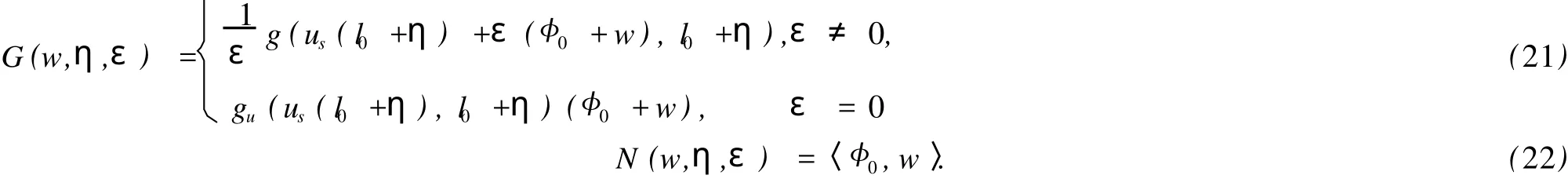
这里us(l0+η)是O(3)对称正解,w∈W;η,ε∈R.显然G(0,0,0)=0,N(0,0,0)=0,方程(21),(22)关于w,η在(w,η,ε)=0(0,0,0)处的Jacobi矩阵为

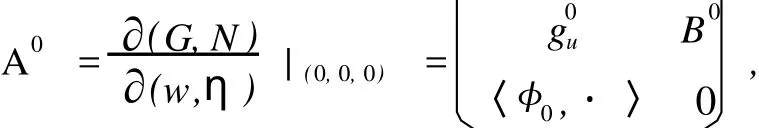
其中B0=[g0uu(us(l0),l0)us′(l0)+g0ul(us(l0),l0)]φ0=[g0uuvl+g0ul]φ0,由于〈ψ0,B0〉=b≠0,φ0∈N(g0u),推出B0∉R(g0u),N(g0u)∩N〈(φ0,·〉)={0}.由Keller引理[19]可知A0非奇异,再由隐函数定理推出

存在光滑解枝(w(ε),η(ε)),∀|ε|<ε0,它们可以用Newton迭代方法求出.于是(us(l0+η(ε)+ε(φ0+w (ε)),l0+η(ε))构成了∑对称解枝.

注1.实际计算时,方程(21)中取ε≠0,故在Newton迭代时不必计算在B0出现的二阶导数.方程(23)在极坐标系下具体化就是如下问题(以q=3为例):

对给定的ε,通过Newton迭代法可求得问题(23)解(us(l0+η(ε))+ε(φ0+w(ε)),l0+η(ε)),当ε从小取到足够大时,就可以用l延拓法在X∑空间中跟踪问题(9)的∑对称解枝(见图2).

图2 q=3,l=1;5;7;10时,问题(1)的O(2)⊕∑1对称正解在(r,θ)平面上的表示Fig.2 TheO(2)⊕∑1symmetric positive solutions to problem(1)forq=3,l=0;1;5;10 on the(r,θ)surface

2.4 数值结果

图2给出了q=3,l=1;5;7;10时,问题(1)的O(2)⊕∑1对称正解在(r,θ)平面上的表示.

[1] HENON M.Numerical Experiments on the Stability of Spherical Stellar Systema[J].Astronom Astrophys,1973,24:229-238.

[2] BYEON J,WANG ZQ.On the Henon Equation:Asymptotic Profile of Ground States I[J].Ann I H Poincare An,2006,23(6): 803-828.

[3] BYEON J,WANG Z Q.On the Henon Equation:Asymtotic Profile of Ground States ii[J].J D ifferential Equations,2005,216 (1):78-108.

[4] GAO D M,PENG S J.The Asymptotic Behavior of the Ground State Solutions for Henon Equation[J].J M ath AnalAppl,2003,278(1):1-17.

[5] PENG S J.Multiple Boundary Concentrating Solutions to Dirichlet Problem of Henon Equation[J].Acta M athem atics Applicatae Sinica English Series,2006,22(1):137-162.

[6] S METSD,W I LLEM M,Su J.Non-radial Ground States for the Henon Equation[J].Comm unications in Contem poraryM athem atics,2002,4(3):467-480.

[7] AMANN H.Supersolution,Monotone Iteration and Stability[J].J D iff Eq,1976,21:367-377.

[8] AMANN H,CRANDALL M G.On some Existence Theorems for Semilinear Elliptic Equation[J].Indian UnivM ath J,1978,27: 779-790.

[9] CHANG K C.Infinite Di mensionalMorse Theory andMultiple Solution Problems[M].Boston:Birkhauser,1993.

[10] STRUWEM.VariationalMethods,A Series ofModern Surveys inMath[M].Berlin:Springer-Verlag,1996.

[11] PAO C V.Block Monotone Iterative Methods for Numerical Solutions of Nonlinear Elliptic Equations[J].Num erM ath,1995, 72:239-262.

[12] DENG Y,CHEN G,N IW M,et al.Boundary ElementMonotone Iteration Scheme for Semilinear Elliptic PartialDifferential E-quations[J].M ath Com put,1996,65:943-982.

[13] CHO I Y S,MCKENNA P J.A Mountain PassMethod for theNumerical Solutions of Semilinear Elliptic Problems[J].Nonlinear Anal,1993,20:417-437.

[14] D I NG Z H,COSTA D,CHEN G.A High-linking Algorithm for Sign-changing Solutions of Semilinear Elliptic Equations[J]. NonlinearAnal,1999,38:151-172.

[15] L I Y,ZHOU J X.A MinimaxMethod for FindingMultiple Critical Points and ItsApplications to Semilinear PDEs[J].SIAM J Sci Com put,2002,23:840-865.

[16] YAO X D,ZHOU J X.A MinimaxMethod for FindingMultiple Critical Points in Banach Spaces and Its Application to Quasilinear Elliptic PDE[J].SIAM J Sci Comput,2005,26:1796-1809.

[17] CHEN C M,XIE Z Q.Search-extension Method forMultiple Solutions of Nonlinear Problem[J].Com p M ath Appl,2004,47: 327-343.

[18] YANG Z H,L I Z X,ZHU H L.Bifurcation Method for SolvingMultiple Positive Solutions to Henon Equation[J].Science in China Series A:M athem atics,2008,51(12):2330-2342.

[19] 杨忠华.非线性分歧:理论和计算[M].北京:科学出版社,2007.

[20] KELLER H B.On NumericalMethods in Bifurcation Problems[M].Berlin:Springer,1987.

Computing theM ultiple Solutions to Boundary Value Problem of Henon Equation on the Un it Ball of Space

L I Zhao-xiang1,YANG Zhong-hua2,ZHU Hai-long3
(1.Com puting M athem atics Departm ent,Shanghai Nor m al University,Shanghai200234,China; 2.Scientific Com puting Key Laboratory of ShanghaiUniversities,Shanghai200234,China; 3.School of Statistics and Applied M athem atics,Anhui University of Finance&Econom ics,Bengbu233030,China)

We apply the bifurcation method to solving theO(3)symmetric positive solutions to the boundary value problem of Henon equation.Takinglin Henon equation as a bifurcation parameter,the symmetry-breaking bifurcation point on the branch of theO(3)symmetric positive solutions is fund via the extended systems.Moreover,the other symmetric positive solutions are computed by the branch switchingmethod based on the liapunov-Schmidt reduction.

Henon equation;symmetry-breaking bifurcation;extended system;branch s witching

O175

A

0253-2395(2010)04-0479-07

2010-01-22;

2010-02-22

国家自然科学基金(10901106);上海重点学科建设项目(S30405);上海市自然科学基金(09ZR1423200);上海师范大学科研项目(SK200936);上海市科委创新项目(09YZ150);上海市教委高校优青培养科研专项基金(RE948);安徽省高等学校优秀青年人才基金(2009SQRZ083)

李昭祥(1973-),男,江苏东台人,博士,上海师范大学数理学院讲师,偏微分方程多解计算.E-mail:zxli@shnu. edu.cn