教学质量评价的模糊数学模型及应用研究

韩欲青

教学质量评价的模糊数学模型及应用研究

韩欲青

(商丘职业技术学院,河南商丘 476000)

在结合实际评估案例的基础上,引进模糊数学模型的方法对高校教师教学质量进行评估,可改进、提高高校传统教学评估体系的有效性,该模型具有广阔的应用前景和方法论价值。

数学模型;教学评估;权重值

当前我国各高校都开始充分认识到教学评估的重要性,逐渐把教学质量评估作为教学管理的日常工作之一来抓。针对高校教师进行的教学质量评估一般通过学生评价、专家评价、同行评价和教师自评四个环节进行,接着综合考量最后的评价结果。但是,目前教学质量评估体系在建立、使用和评估结果分析的过程中仍然存在一些没有完全解决的问题,比如评估理论的研究、评估方法的更新、评估数据的分析等等。这些问题都不同程度上影响着教学质量评价功能的实现和教师潜在能力的挖掘。为了实现教学评价体系的指标全面性、指标权值分配的均衡合理性,更加全面地、动态地评价一个教师的真实教学质量,笔者借助模糊数学方法建立一个教学过程模糊评价模型,在实践中取得了比较好的效果。

一、评价因素集U

本模型不同于传统的单纯的平均算法,而是使用了模糊综合评判的方法,该方法相对普通的评估方法更能权衡各类因素,确保信息最大程度保留,真实地使参与评估过程当中的每一个人的评价信息都能够发挥相应的作用,做到全面和动态的评价。要实现该评价模型的功能目标,即全面评价教师的教学质量,首先必须确定评价指标体系。目前的调查结果发现大多数院校使用的还是定量教学质量评估指标体系,也就是对教师的教学内容、教学方法、教学态度、教学效果和讲授能力等内容进行评估。下表列出的是本评估模型采用的教学质量评估体系的一级指标和二级指标。

一级指标二级指标教学态度A(0.15)课下辅导认真A1(0.3);热爱教学,有责任心A2(0.3)备课充分,上课熟练A3(0.2);按时上下课,不缺课A4(0.2)

一级指标二级指标教学内容B(0.25)观点阐述准确B1(0.3);详略得宜,进度适当B2(0.2)重难点突出B3(0.3);联系实际,针对性强B4(0.2)教学方法C(0.3)因材施教,善于启发C1(0.2);方法合宜,形式活泼C2(0.15)强调实践,注重能力C3(0.3);生动活泼,由浅入深C4(0.35)讲授能力D(0.17)层次分明,逻辑清晰D1(0.3);板书整洁,语言清晰D2(0.2)语速和音量适中D3(0.3);语言精练,有吸引力D4(0.2)教学效果E(0.13)学生学习效果明显E1(0.3);学生成绩明显提高E2(0.4)激发学生学习兴趣E3(0.2);课堂提问、作业批改E4(0.1)

根据该表提供的一级指标和二级指标,可以确定下列因素集是模糊评价模型必须纳入的各要素(也可以在各个学校和部门的实际使用过程中,酌情增减必要的考察因素)

二、评语集V

V={优,良,中,差}。

三、模糊评价矩阵

由于以上的因素集和评语集可以得出相应的模糊评价矩阵。具体方法我们可以结合一个案例来说明。

假设有100名教师参与教学评估,对一级指标教学态度的某项二级指标进行了评价,其中判为优的有60名,良有20名,中有15名,差有5名。那么我们可以先把它们量化为:优:60/100,良:20/100,中:15/100,差5/100,于是可以构成教学态度的某项的行矩阵为(60/100,20/100,15/ 100,5/100),由此可以类推教学态度中其他其他二级指标的行矩阵,最后我们得到了关于教学态度的模糊评价矩阵R1为:

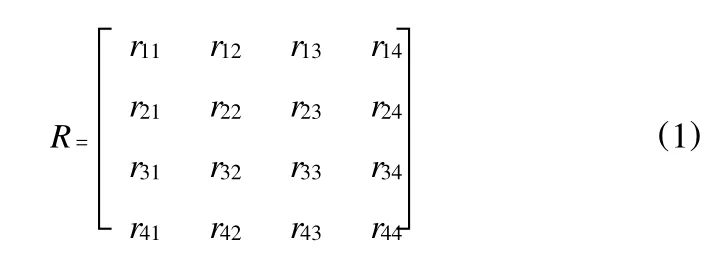
以此类推可以得到B,C,D,E各评价因素的模糊评价矩阵R2,R3,R4,R5。

四、权重值分配

确定各类个因素的权重分配状况就是确定个因素对教师工作效果的隶属度,根据对10余所高校,数十名专家学者的调查结果,给出以下的权重值分配状况,经过一致性检验获得无逻辑错误的结果。

M1={0.3,0.3,0.2,0.2};

M2={0.3,0.2,0.3,0.2};

M3={0.2,0.15,0.3,0.35};

M4={0.2,0.15,0.3,0.35};

M5={0.3,0.4,0.2,0.1};

M0={0.15,0.25,0.3,0.17,0.13}

五、综合评判算法

由于实际的教学工作中包含的实际影响教学评估的因素比较多,层次也比较多,哥哥因素又会包含若干个子因素,所以诸因素要分层分级进行评价,先从最低一级开始,逐步向上,一直到最高以及评价,从而得到最终的结果。

针对上述模型,首先由最低一级,也就是二级因素开始,得到二级因素的评价矩阵:

Z1=M1·R1,Z2=M2·R2,Z3=M3·R3,Z4=M4· R4,Z5=M5·R5。

其中Z1,Z2,Z3,Z4和Z5分别为4列的行矩阵,再由二级因素的评价矩阵得出一级因素的评价矩阵,具体方法如下:

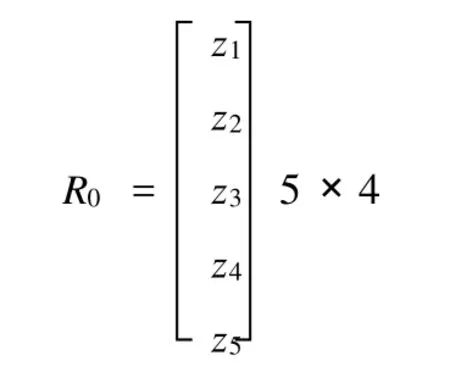
再由R0得出一级相应评价矩阵Z,从而得到最终的评估结果。具体而言,就是Z=M0·R0={z1,z2,z3,z4}。例如,通过矩阵相乘运算得出:Z={0.6792,0.2381,0. 0584,0.0243},然后根据最大隶属度原则,在{0.6792,0. 2381,0.0584,0.0243}中最大的数为0.6792所对应的评语集等级为“优”,那么我们对该教师的评估值为优等级。

如果想得到具体的评分结果,那么在上例中可以知道最终得分是:

0.6792 ×95+0.2381×85+0.0584×75+0.0243×65 =90.1分,那么该教师最后的课堂教学评价得分为90.1分。这里假设学生对教师定性的评估为优、良、中、差的具体分数为:{优,良,中,差}={95,85,75,65}。

综上模型和案例应用可以看到采用模糊综合评估的方法,在实际的教学评估过程中,确定了不同的评价因素的均衡分布和权重值,使得评估的结果更加全面,更加客观,也能够在一种动态平衡中综合反映每一名教师的真实教学水平和教学质量,本方法更便捷的特点还在于根据该方法得出的教学质量评价的模糊数学模型可以很容易在计算机上运算,这样也节省了大量人力、物力和时间,因此,这是一个应用前景很广泛的数学模型。

[1] 冯永潮.提高教育评价科学性的基本途径[J].教育研究,2002(02).

[2] 汤先君.浅谈数学新课程教学的几种评价方法[J].教育研究,2005(08).

[3] 杨伦标.模糊数学原理及其应用[M].广州:华南理工大学出版社,1998.

[4] 刘琳,刘志新,吴忠强.高校教学质量模糊评价体系及实践[J].石家庄经济学院学报,2006(03).

责任编辑:何玉付

G423.04

A

167128275(2010)0520027202

2010206211

韩欲青(19712),女,河南商丘人,商丘职业技术学院讲师。研究方向:数学课程教学论。