基于NicheGA和FPN的独立全局约束Web服务组合优化方法
冯英华,许志才,王 娟
(1.安徽理工大学 理学院,安徽 淮南232001;2.滁州学院 数学系,安徽 滁州239012;3.淮南联合大学 基础部,安徽 淮南232001)
基于NicheGA和FPN的独立全局约束Web服务组合优化方法
冯英华1,3,许志才2,王 娟1
(1.安徽理工大学 理学院,安徽 淮南232001;2.滁州学院 数学系,安徽 滁州239012;3.淮南联合大学 基础部,安徽 淮南232001)
针对独立全局约束Web服务组合问题,本文提出了利用模糊Petri网(FPN)来建模,将寻找可行的服务组合问题转化为寻找FPN模型中可发生序列问题,从而把求解最佳服务组合问题转化为在FPN模型中寻找信任值最大的合法发生序列问题.然后利用小生境遗传算法(NicheGA)来寻找最优合法序列,以获得最优的组合服务。最后实验仿真结果表明该方法既减少了计算时间又能找出更多的最优解。
模糊Petri网,小生境遗传算法,Web服务组合,优化
0 引言
目前,服务组合已成为一个研究热点.组合方法可分为人工合成,半自动合成和全自动合成[7].由于人工合成不能很好地满足现实的期望,而全自动合成的过程又非常复杂,所以大部分关于服务组合的应用和研究都是半自动合成.一个服务发现的方法要么面向句法要么面向语义.而面向语义的方法的服务查全率比面向语法的方法要高[8].
在使用者的要求[5]中,用约束条件来准确描述需要找的服务.一般有两种类型:局部约束和全局约束.前者是用来约束单个服务,比如购买联想电脑,那么联想电脑就是局部约束,后者是用来约束多个服务,比如买电脑时,买家收到电脑的时间≤电脑上保险的时间≤电脑组装时间,这就是全局约束.全局约束可分为严格依赖条件和严格独立条件.一个全局约束是依赖的,如果一旦其中的一个属性被赋值,那么所有剩下的受限制属性的值都能唯一确定.满足严格依赖全局约束的组合问题可以用多项式时间[9]的方法容易得解决.
任何全局约束不是严格依赖就是严格独立的,而本文研究的是严格独立全局约束下的Web服务组合问题.
1 基本概念
本文将基于模糊Petri网推理来解决Web服务组合问题.因此,首先介绍一些模糊Petri网的相关概念.
定义1FPN是一个八元组[2]:FPN=(P,T,D,I,O,f,α,β),
其中:
P={P1,P2,…,Pn}是库所节点的有限集合,用来表示模糊命题;
T={T1,T2,…,Tn}是变迁节点的有限集合,用来表示规则的实现;
D={d1,d2,…,dn}是一个有限命题的集合;
|P|=|D|;
I:T→P∞是一个输入函数,映射一个变迁到它的输入库所集合;
O:T→P∞是一个输出函数,映射一个变迁到它的输出库所集合;
f:T→[0,1]是一个函数,映射变迁到一个0~1的数值,用来表示变迁对应的推理规则置信度(Confidence Factor);
α:P→[0,1]是一个函数,映射库所到一个0~1的数值,用来表示该库所对应的命题成立的真实度,即
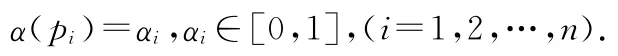
β:P→D是一个函数,映射库所对应的命题,即

当用FPN进行模糊推理时,一个库所表示一个命题,一个变迁表示一条模糊推理规则,即两个命题之间的因果关系.每个变迁有一个置信度,表示推理规则的可信度.
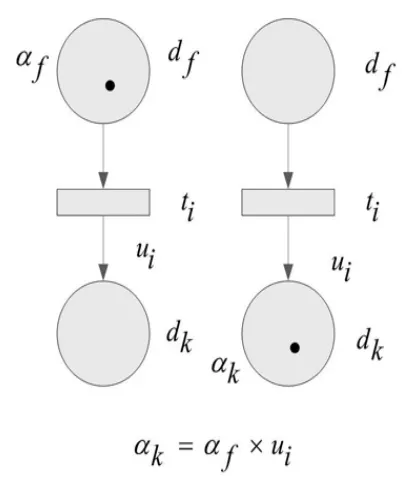
图1 基本FPN推理过程

图2 类型1的FPN推理过程

图3 类型2的FPD推理过程

图4 类型3的FPN推理过程
FPN的基本推理规则的形式是[2]:
Ri:IFdfTHENdk(CF=ui),这里df,dk是两个命题。推理过程可以建模为图1,其中命题df,dk用库所pf和pk表示,命题df的真实度为αf.命题之间的因果关系用变迁ti表示,它的置信度为ui.当变迁触发后,命题pk的真实度为αf×ui.一条推理规则若包含“and”或者“or”连接符,就称为组合产生式规则.组合产生式规则被分为基本的3类:
类型1:Ifdf1anddf2and…dfnThendk(CF=ui),这dfk(1≤k≤n)∈D。推理过程可以建模为图2,推理后命题dk的真实度是 min(αf1,αf2,…,αfn)×ui。
类型2:IfdfThendk1anddk2and…dkn(CF=ui),这里dki(1≤i≤n)∈D,推理过程可以建模为图3。
类型3:Ifdf1ordf2or…dfnThendk(CF=ui),这dfk(1≤k≤n)∈D,推理过程可以建模为图4.
2 基于FPN的服务组合模型的建立
本文采用FPN对独立全局约束的服务组合进行建模.服务组合的FPN模型中库所代表服务,变迁代表全局约束条件,变迁的置信度代表该变迁前集所代表的服务对变迁后集所代表的服务的信任值.服务组合的获得包含三个阶段:候选服务的获得,约束条件的识别和最优组合的获得.基于独立全局约束服务组合的FPN建模过程如下:
(1)先找到候选服务[1],用库所来表示它们,然后把具有相同功能性质的候选服务放在同一水平线上.
(2)服务间的独立全局约束条件用变迁来表示.若两个服务间存在独立全局约束条件,则在它们和变迁之间用弧线连接.变迁的置信度表示该变迁前集所代表的服务对它后集所代表的服务的信任值.
(3)利用(1)和(2)得到独立全局约束服务组合的模型.那么寻找可行的服务组合问题即可转化为寻找FPN模型的可发生序列问题.从而最佳服务组合也就是模型中信任值最大的可发生序列.
3 基于小生境遗传服务组合最优化算法
本文充分利用FPN模型,对FPN模型中的变迁进行编码[5].具体而言,文中将发生序列作为染色体,每个可发生序列代表可行的Web服务组合.这样寻找可行的服务组合问题即可转化为寻找FPN模型的可发生序列问题.如果只是用FPN来做组合问题,当组合规模相当大的时候会非常复杂.如果只采用GA,那么搜索具有相当大的随机性[5],所以文中的方法将两者结合起来同时考虑,这样既降低了计算的复杂性又降低了搜索的随机性.
遗传算法[4]是模拟自然界生物群体进化过程的一种随机优化方法,具有不依赖于问题模型的特性、寻优过程的自适应性、隐含的并行性以及解决复杂非线性问题的鲁棒性等优点,并在许多复杂优化问题都找到了令人满意的解。但大量的经验表明,标准遗传算法存在早熟收敛现象和后期搜索速度慢的缺点[3].在大量的实际优化问题的求解计算中,不仅要求在可行域内寻找全局最优解,而且往往需要搜索多个全局最优解和有意义的局部最优解,从而为决策者提供多种选择或者多方面的信息。为了能够搜索到全部全局最优解和尽量多的局部最优解,本文采用的是基于FPN和NicheGA的独立全局约束服务组合的最优化方法,算法如下:
(1)染色体编码
设置进化代数计数器t←1,给定一距离L.在FPN模型中,如果存在一组发生序列σ=t1t2…tn-1tn,使得M0[σ>Mf,且σ是满足组合服务要求的可发生序列,那么就将σ当成一个染色体,其中M0是初始序列,Mf是末序列,t1,t2…tn-1,tn∈T.
根据服务进程的要求,随机选择M个满足条件的可发生序列作为初始群体P(t).
(2)个体评价
根据FPN的推理规则可以计算出每个染色体σ的信任值TD(σ),TD(σ)=f(t1)f(t2)…f(tn),因为 NicheGA要求越优的解具有的适应度越大[6],所以适应度函数定义为:

(3)根据各个可行序列的适应度对其进行降序排序,记忆前N个可行序列(N<M).
(4)选择运算

对群体进行单点交叉运算,步骤如下:
1)对群体中的可发生序列进行两两随机配对。
2)对每一对相互配对的可发生序列,随机设置某一变迁之后的位置为交叉点.
3)对每一对相互配对的可发生序列,按照设定的交叉概率pc在其交叉点处相互交换部分变迁序列,从而产生出两个新的变迁序列.
4)按照FPN推理规则,检验由3)产生的新变迁序列是否为可行序列,若是则保留,否则排除.
(6)变异运算
对群体进行均匀变异运算,步骤如下:
“天色已晚,回去吧。”江南垂柳岸,杨公子一身白衣在前,我走在他身后,耳边飘来戏台上的唱曲“错!错!错!”
1)依次指定发生序列中的每个变迁为变异点.
2)对每个变异点,以变异概率pm从对应变迁的取值范围内取另一变迁来替代原有变迁,从而得到新的变迁序列.
3)检验由2)产生的新变迁序列是否为可行序列,若是则保留,否则排除.
(7)小生境淘汰运算
将第(6)步得到的M个发生序列和第(3)步所记忆的N个发生序列合并在一起,得到一个含有M+N个可行序列的新群体;对这M+N个可行序列,按照下式求出每两个可行序列σ和σ*之间的海明距离,其中是不同属性的候选服务的个数:
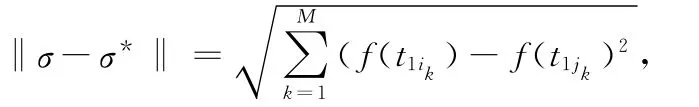
其中f是用来表示变迁对应的推理规则置信度.
当‖σ-σ*‖<L时,比较个体σ和个体σ*的适应度大小,并对其适应度较低的个体处以罚函数,Fmin(σ,σ*)=10-3.从而在L内只保留一个优良的可行序列。
(8)依据这M+N个发生序列的新适应度对各个序列进行降序排序,记忆前N个可行序列.
(9)终止条件判断.若不满足终止条件,则:更新进化代数计数器t←t+1,并将第(8)步排序中的前 M个发生序列作为新的下一代群体,然后转到第(4)步;若满足终止条件,则:输出计算结果,算法结束.
4 实验仿真结果
本文提出了基于FPN和NicheGA的独立全局约束服务组合优化方法,这种方法不仅利用了FPN在描述多属性混合约束问题上的优越性,而且充分利用了Petri网的特点.理论上,这种方法对分析独立全局约束服务组合问题是有效的.既避免了Petri网组合的复杂性又避免了GA的随机性和早熟收敛现象等缺陷.接下来,我们利用实验仿真来分析该方法的可行性.具体步骤如下:
(1)在服务库里寄存大量的服务,个数为50至500;
(2)设置服务的功能和约束条件,每个服务包括3到7个服务组件;
(3)实验仿真平台为 Winxp,Dell optiplex320,内存1G,L=0.001Matlab6.5.
对于一个给定的服务要求,分别利用GA&APN和NicheGA&FPN方法,我们从服务库中找出可行的候选服务,然后在不同的候选服务数量下比较它们的时间效率和查找可行解的比率.

图5 两种算法时间比较
在图5中,横坐标表示服务的数量,纵坐标表示两种方法的执行时间,由图中可以看出本文的方法比GA&APN方法的时间效率高.而且随着服务数量的增多,这种优势越明显.
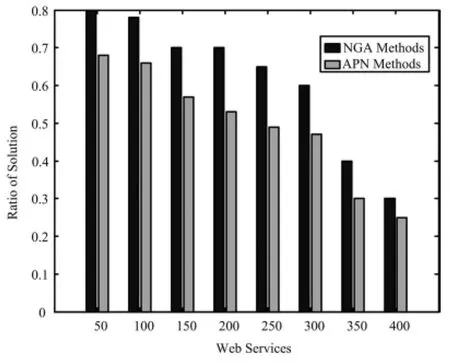
图6 两种算法的查找可行解的比率比较
在图6中,横坐标表示服务数量,纵坐标表示两种方法的查找可行解比率.可行解比率是指找到的可行服务的数量与所有可行服务的数量的比值.由图可以看出本文的方法比NG&APN方法的可行解比率远比APN方法要高.
5 总结
研究独立全局约束服务组合问题,现有的方法有Greedy、Approximating和GA&APN.前两种方法虽然它们在解决约束问题上有很好的效果,但是对于处理多属性和混合约束问题,它们存在缺陷.而后一种方法中的遗传算法存在早熟收敛现象和后期搜索速度慢的缺点.
本文采用模糊Petri网对独立全局约束的Web服务组合进行建模,然后利用小生境算法来寻找最优解,这样克服了标准遗传算法早熟收敛现象和后期搜索速度慢的缺点,而且能够搜索到全部全局最优解和尽量多的局部最优解.最后的仿真结果表明这种方法不仅节省了时间而且搜索到了更多的最优解.
[1]Nalaka Gooneratne,Zahir Tari.Matching Independent Global Constraints For Composite Web Sdrvices,WWW2008,765-774,2008.
[2]葛敬军,黄 华,胡建明.面向语义Web服务组合的模糊Petri网推理算法[J].计算机科学,2009,36(9):121-122.
[3]赵苗,齐丽丽,李建晶.基于小生境技术的遗传优化算法改进[J].计算机科学,2009,28(3):161-163.
[4]侯格贤,吴成柯.遗传算法的性能分析[J].控制与决策,1999,14(3):257-260.
[5]Fang,X.W,C.J.Jiang,and X.Q.Fan.Independent global constraints-aware web service composition optimization[J].Information Technology Journal,2009,8(2):181-187.
[6]郝 冬,蒋昌俊,林 琳.Petri网和遗传算法在FMS中的应用[J].中国计算机报,2005,28(2):202-208.
[7]陈丁建.基于语义的 Web服务发现和组合的研究[D].西北工业大学博士论文,2006,21(3):23-24.
[8]I.Elgedawy,Z.Tari,and M.Winikoff.Exact Functional Context Matching for Web Services[R].In Proceedings of the 2nd International Conference on Service Oriented Computing,pages,143-152,2004.
[9]N.Gooneratne,Z.Tari,and J.Harland.Matching Strictly Dependent Global Constraints for Composite Web Services[R].In Proceedings of the European Conference on Web Services,pages 139-148,2007.
[10]Dong-Her Shih,Hsiu-Sen Chiang,and Binshan Lin.A Generalized Associative Petri Net for Reasoning[J].IEEE Transactions Knowledge and Data Engineering,VOL.19(9):1241-1251,2007.
Optimization Method of Independent Global Restriction Web Service Combination Based on Niche GA and FPN
Feng Yinghua1,3,Xu Zhicai2,Wang Juan1
(1.School of Science,Anhui University of Science and Technology,Huainan 232001,China;2.Department of Mathematics,Chuzhou University,Chuzhou 239012,China;3.Department of Basic Courses,Huainan Union College,Huainan 232001,China)
For independent global restriction Web service combination,the paper suggests using fuzzy Petri net(FPN)for modeling,which changes finding feasible service combination into finding the possible sequence in the FPN model,thus bringing seeking best service combination into finding the legal sequence of the largest trust value in the FPN model.Niche genetic algorithm(Niche GA)is then used to find the optimal legal sequence in order to obtain optimal combination service.The experimental results show that the method can not only reduce the computational time but also obtain more optimal solutions.
fuzzy Petri net;Niche genetic algorithm;Web service combination;optimization
TP391.9
:A
:1673-1794(2010)05-0023-04
冯英华(1979-),女,硕士生,讲师,研究方向:Web服务,Petri网及应用。
安徽省高校省级自然基金项目(KJ2010B310)。
2010-06-11

