基于动态MAUT的油气勘探风险决策模型研究
王 众,张哨楠,匡建超
(成都理工大学能源学院油气藏地质及开发工程国家重点实验室,四川 成都610059)
油气勘探属于典型的 “三高一长” (高投入,高风险,高产出,长周期)项目,作为石油公司的一项主要投资活动,勘探项目的风险决策一直是倍受关注的研究领域。如何从效益-风险的角度,对勘探目标进行科学决策,降低风险、提高经济效益,已成为我国油气工业发展面临的瓶颈问题。然而,传统决策方法往往以期望收益最大化为决策准则,忽视了决策者的风险承受能力和风险偏好。随着以风险偏好为核心的现代效用理论的提出,风险决策准则逐渐发展为期望效用最大化。[1,2]20世纪70年代,Keeney提出的多属性效用理论 (MAUT),又将效用决策由单属性发展为多属性,较好地解决了多目标决策问题。20世纪90年代以来,以Walls和Suslick为代表的学者,又将MAUT引入油气领域,均取得了不错效果。[3]
笔者以Suslick提出的MAUT决策框架为基础,从风险-收益的角度出发,凝练出 “地质风险”、“市场风险”和 “经济收益”3大属性,并设定属性权重的变化范围,对属性进行动态赋权,构建了基于动态MAUT的勘探风险决策模型。该方法不仅充分考虑了决策者的风险偏好,且能够反映决策结果的稳定性,帮助决策者以动态、全面的眼光进行风险决策分析,从而使得决策过程更加科学,结果更加合理。
1 多属性效用理论 (MAUT)
多属性效用理论 (Multi-Attribute Utility Theory,MAUT)是一种结构化、逻辑化、系统化的决策分析理论。通过多属性效用函数,将决策者对待风险的态度、经验及判断能力等主观因素与方案的客观损益有机结合在一起,以效用的期望值作为决策依据。MAUT基本原理,就是首先通过效用的分解,得到一系列与目标相关的单一属性;然后计算单一属性的效用值及其权重;再根据各属性之间的相关性选择适当的模式,再对其进行组合,得到反映决策者偏好的多属性效用函数;最终,根据总效用值的大小进行方案优选。
2 基于动态MAUT的油气勘探决策模型
(1)属性的确定及效用函数生成
油气勘探属于典型的高风险、高收益项目。笔者在总结前人研究的基础上,充分考虑勘探项目的风险与收益,以 “地质风险”、 “市场风险”和 “经济收益”作为决策模型的三大属性。对于“地质风险”,笔者以地质成功概率为评估标准,成功概率越大,效用值越大;对于 “市场风险”,以净现值标准差为评估标准,标注差越大,属性越小;对于 “经济收益”,以最大期望投资收益率为评估标准,期望收益率越大,属性值越大。
(2)多属性效用函数的确定
设方案集A= {A1,A2,A3,…,Am},各方案多属性效用函数为Uj(X),j=1,2,…,m。一般而言,将单属性效用复合为多属性效用,可以分为加法模式和相乘模式两种:
① 若属性之间相互独立,使用加法模式:

式中:ki—第i个属性的权重,且1。
② 若属性之间存在相关性,使用相乘模式:

式中:ki——第i个属性的权重 (0≤ki≤1),且;k为常数,且有

(3)属性权重的确定
属性权重的确定,一直是MAUT在实际应用中的一个难点。传统赋权方法,一般分为静态专家赋权和动态随机赋权两大类。然而,笔者认为,这两种方法各有优缺点:静态专家赋权,虽考虑了专家经验,但难以取得统一、精确的结果;动态随机赋权,虽然能对决策结果的稳定性进行检验,但某些随机确定的权重值,明显超出了合理范围,缺乏科学性。基于此,本文在动态赋权的基础上,融入专家经验,设定各属性权重的分布形式和变化范围,在此范围内进行动态赋权。该方法不仅充分考虑了专家经验,同时也能够反映权重变化对决策结果的影响,有利于决策者以全面、动态的眼光做出科学的决策。
(4)最优方案的确定
首先考虑属性之间相互独立的情况,若仿真n次,共得到p组总效用集 {U1(X),U2(X),…,Um(X)}1,…… ,{U1(X),U2(X),…,Um(X)}p。将每一组效用集中的方案,按照效用值大小排序,这样将得到p种排序情况:若方案j排第一、第二,……、第m的次数分别为t1,t2,则方案Aj为最优方案、优方案、……、最差方案的概率分别为t1/p,t2/p,…,tm/p;同理,可求出其余方案的排序概率,并将这些概率描绘到图上,便于观察各方案排序由于属性权重不同而变化的情况。类似的,再考虑属性间相关的情况。最后,综合考虑独立和相关两种情况,选择最优方案。
3 应用实例
为了检验模型的实际应用效果,笔者以文献[9]的数据为基础,挑选出 “地质成功概率大于0.6”且 “最大预期现金流大于15亿元”的5个勘探项目组成备选方案集,运用动态MAUT风险决策模型对其进行决策分析。决策的结果合理,符合客观实际。
(1)构造效用函数。通过对某油气勘探开发公司决策人员的风险偏好问卷调查 (具体过程请参见文献 [2]),确定了决策者对于属性集X={地质储量、经济效益、技术风险}中各属性的3个效用确定当量点,并根据公式

式中,a、b—常数,c—风险厌恶因子。该效用函数的确定取决于式 (4)中的3个待定参数a、b和c。通过确定函数的3个确定当量点,即效用最大点 (u=1)、效用最小点 (u=0)以及中位值点(u=0.5),联立3个方程,便求出唯一的效用函数表达式。得出各属性的效用函数表达式,结果见表1。

表1 各属性的效用确定当量点
(2)计算各方案的单个属性效用值。根据表1中求出的各属性效用函数,计算各勘探项目各单一属性的效用值,计算结果见表2。
(3)确定各属性权重的分布规律和变化范围。文本请专家对属性进行赋权,综合专家意见,得出各个属性权重的分布规律和变化范围见表3。
(4)计算各方案的总效用,挑选最优方案。笔者运用Matlab进行相应的程序设计,考虑属性独立和相关两种状态,分别仿真10000次,得出各方案的排序情况,见图1和图2。

图1 属性独立的方案排序图
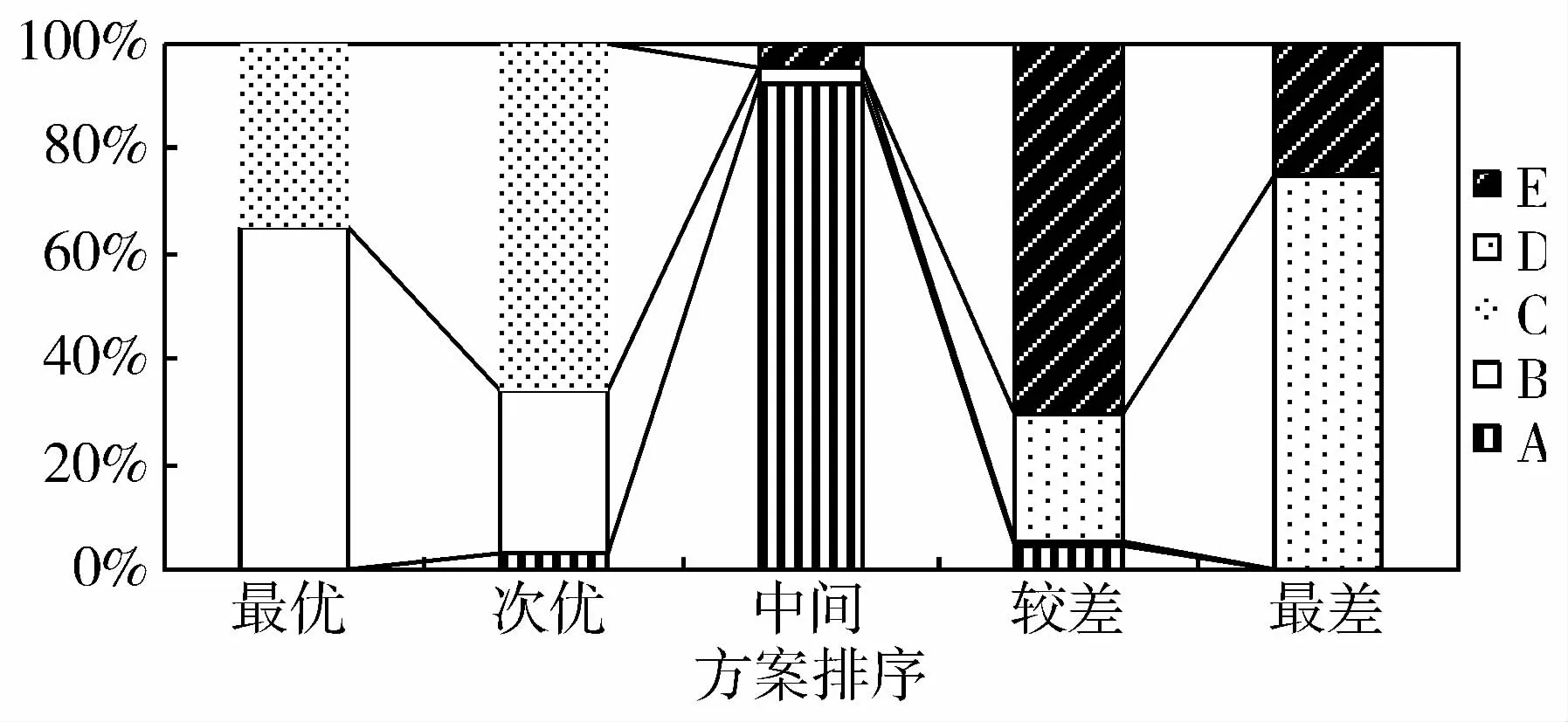
图2 属性相关的方案排序图
由图1、图2,可以很清晰的观察由于属性权重变化而导致各个方案排序变化的情况。根据图1分析:B作为最优方案的概率最大 (57%),但不稳定,受到属性权重变化的影响较大,有大约15%和4%的可能成为中间和较差方案;C为最优方案的概率略低于B(42%),但作为次优方案的概率最高,同时稳定性较高 (为中间方案的概率小于4%,为较差和最差方案的概率为0)。根据图2分析:B依然作为最佳选择,其概率更是高达65%,同时稳定性大大提高;C作为最优方案的概率虽然有所下降,但为次优方案的累积概率已经高达99.9%。
综合考虑图1、图2,笔者认为,若决策者认为B方案排序的波动在承受范围内,则B为最优方案,C为次优方案;若决策者对稳定性要求较高,则C为勘探投资的最优方案。
4 结语
油气勘探的风险决策是一个系统、复杂的决策过程。多属性效用理论 (MAUT)借助效用函数来表示各属性对备选方案的贡献,有助于决策者考虑、分析油气勘探过程中涉及的相关因素以及决策者的风险偏好。此外,结合动态赋权,使得决策者能够了解各个方案受属性权重变化的影响,帮助决策者以全面动态的眼光来进行决策分析。应用实例结果表明,基于动态MAUT的决策模型,能够有效地帮助决策者对于油气勘探项目,做出科学、合理的决策。

