余导子与余积分及其性质
代瑞香,刘超
(石河子大学师范学院数学系,石河子 8 32003)
余导子与余积分及其性质
代瑞香,刘超
(石河子大学师范学院数学系,石河子 8 32003)
根据余环上的余导子与余整合的定义及性质,给出了 T-余单子上的余导子、余整合的定义,并在它们构成的阿贝尔群之间构造了一个同构关系;基于代数模理论的知识,在余环的余可分性质基础上刻画了余单子余可分、忘却函子可分与余积分存在之间的相互等价关系。
T-余单子;余导子;余积分
Abstract:The definions of coderivations and cointegrations ofT-comonads are given in the paper based on the definition and property of coderivations and cointegrations,and the equivalent relation of coseparable comonads,separable forgetful functors and the existence of cointegral from coseparable coring are given according to the algebra module theory.
Key words:T-comonads;coderivations;cointegral
1956年Mac Lane[1]最早指出所有的标准预解式都可从伴随对中得到,其后Godement[2]运用余单子把这些预解式系统化,Huber[3]给出了一些可由余单子定义的导出函子的例子,并在一般的阿贝尔范畴中研究了这些函子的简单的预解式。之后,Hilton提出了“是否任意的单子都可从伴随中产生?”。Barr和Beck[4]证明了预解式可从单子中导出,并指出余单子也可用于非阿贝尔范畴中;Blackwell等[5]详细介绍了2-维的单子理论。Moerdijk[6]中介绍了张量范畴上的 Hopf单子,并研究了 Hopf单子的一些性质,包括它的代数结构和Hopf代数结构。
缠绕结构可被理解成双代数的总结与归纳,在很多应用中,特别是在数学物理和非交换几何中,它可被看作是非交换流形的对称。从 Hopf代数的观点看,缠绕结构的引入把研究了30多年的 Hopf模的各种范畴统一化了。代瑞香等[7]和王顶国等[8]研究了将代数和余代数的缠绕结构上的一些结论推广到单子和余单子的缠绕结构上,代瑞香等[9]讨论了余单子上的类群元的有关性质,并定义了缠绕结构之间相容的定义和等价条件。
本文拟在上述研究的基础上给出 T-余单子上的余导子和余整合的定义,构造它们构成的阿贝尔群之间的同构关系,并探讨 Frobenius函子、函子可分和 T-余单子余可分的等价命题。
1 预备知识
定义1[10]设D是任一范畴,自同态函子End D是一个严格的Monoidal范畴,D上的单子是指三元结构(T,μ,η),其中 T:D→D是一个函子,μ:T2→T和η:idD→T是自然变换,满足μX·ηTX=idTX=μX·ηX。
设(T,μ,η)为 D上的单子,T-模是指(M,r),其中M∈obj(D)和 r:T(M)→M为 D中的态射,使得
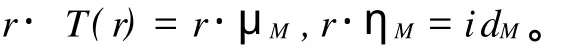
再设(M,r)、(N,s)为2个 T-模,态射 f:M→N称为 T-线性的,若 f·r=s·T(r),这样的 f也称为T-模态射。
定义2[11](G,Δ,ε)称为范畴 D上的余单子,若函子 G:D→D及自然变换Δ:G→GG和ε:G→id,满足 GΔ·Δ=ΔG·Δ;εG·Δ=Gε·Δ=idG。
类似文献[11]可定义:
定义3 设(T,μ,η)是范畴 D上的单子,右 T-模 M ∈End(D)称为实(firm)右 T-模,若ωM+:M T→M为双射,其逆记作M→M T。
定义4 设(T,μ,η)是范畴 D上的单子,C∈End(D),T-余单子C是指
C为实 T-双模态射;(T,T)-双线性态射
ΔC:C→C2,εC:C→T满足 CΔC·ΔC=ΔCC·ΔC;
CεC·ΔC=;Cεc·ΔC=。
事实上,T-余单子C即为 T-模范畴上的余单子。
2 余导子及其性质
本节将根据余环上余导子与余整合的定义及性质,给出 T-余单子上余导子、余整合的定义,并在它们构成的阿贝尔群之间构造一个同构关系。
定义5 设C为实 T-余单子,给定2个C-双余模(M,ρM,λM)和(M,ρN,λN),自然的 T-双线性态射g:M→C称为余导子,若ΔC·g=gC·ρM+Cg·λM,余导子 g称为内余导子,若存在自然的(T,T)-双线性态射γ:M→T使得
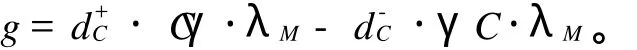
所有 M到C的余导子构成的阿贝尔群记作Coder(M,C)。
定义 6 设(M,ρM,λM),(N,ρN,λN)是 2 个 C-双余模,N到M的余整合是指自然的(T,T)-双线性态射 f:N→CM,满足ΔCM ·f=Cf·λN+CλM·f。
余整合 f称为内余整合,若存在自然的(T,T)-双线性态射φ:N→M满足Cφ·ρN=ρM·φ;
f=Cφ·λN-λM·φ。
所有N到M的余整合构成的阿贝尔群记作Coint(N,M)。
根据上述定义有下面的定理成立:
定理 1 对任意的 C-双余模(M,ρM,λM),有自然同构Φ:Coint(M,C)→Coder(M,C).若限制在内子群上,同样有同构InCoint(M,C)≌InCoder(M,C)。
3 余积分及其性质
下面在余环的余可分性质[12]的基础上讨论余单子余可分、忘却函子可分与余积分存在之间的相互等价关系。依据余环上余积分的定义及性质,下面给出余单子上余积分的定义及性质。
定义7 设 T为范畴D上的单子,C为 T-余单子,若存在(T,T)-双线性自然变换γ:→T满足γ ΔC=εC;·Cγ·ΔCC=·γC·CΔC,则称γ:C2→T为 T-余单子C的余积分。
定理2 设 T为范畴D上的单子,C为 T-余单子,忘却函子 F:TMC→MT可分当且仅当 T-余单子C存在余积分γ:C2→T。
证明:1)必要性。
设 F:TMC→MT有右伴随函子 G:MT→TMC,令单位 φ:→GF,φ(N)GFN。由于 F可分,则存在(T,T)-双线性自然变换v:GF→idTMC使得vN·φN=idN。又余单子 C可看作 C-余模,则 φC=ΔC,从而有相应的 vC:C2→C使得vC·ΔC=idC。


[1]Mac Lane S.Homologie des anneaux et des modules[M].Louvain:Colloque de topologie algebrique,1956.
[2]G odement R.Theorie des faisceaux[M].Paris:Hermann,1958.
[3]Huber P J.Homotopy theory in general categories[J].Math Ann,1961(144):361-385.
[4]Barr M,Beck J.Acyclic models and triples[M].New Y ork:Springer-Heidelberg,1966.
[5]Blackwell R,Kelly G M,Power A J.Two-dimensional monad theory[J].J Pure Appl Algebra,1989,59:1-41.
[6]Moerdijk I.Monads on tensor categories[J].J Pure Appl Algebra,2002,(168):189-208.
[7]代瑞香,刘超,王顶国.缠绕结构与缠绕模[J].石河子大学学报:自然科学版,2008,26(1):106-109.
[8]王顶国,代瑞香.单子和余单子的缠绕结构[J].数学学报,2008,51(5):927-932.
[9]代瑞香.余单子的类群元及其性质[J].长春师范学院学报:自然科学版,2009,28(3):11-12.
[10]Bruguieres A,Virelizier A.Hopf Monad[J].Adv Math,2007,215(2):679-733.
[11]G omez-T orrecillas J.Comonad and Galois corings[J].Applied categorical Structure,2006,14(5/6):579-598.
[12]Brzezinski T,Wisbauer R.Corings and Comodules[M].London:Cambrige University Press,2003.
Properties of Coderivations and Cointegrals
DAI Ruixiang,LIU Chao
(Department of Mathematics,Teachers College,Shihezi University,Shihezi,832003,China)
O153.3
A
1007-7383(2010)05-0658-03
2009-09-27
代瑞香(1980-)女,讲师,从事环与代数研究;e-mail:dairx129@163.com。

