桥梁壅水的计算分析
李建梅 广东省水文局梅州分局 514000
桥梁壅水的计算分析
李建梅 广东省水文局梅州分局 514000
建桥后桥墩束窄了河道的过流面积,使桥位上游水位抬高,产生桥前壅水现象。桥前壅水的高度直接影响其上游两岸人民的生命财产安全,因此桥梁壅水计算有着重要的实际意义。本文主要采用水面曲线法以及堰流公式法对桥梁壅水进行了对比计算和分析。
1、概述
桥梁建成后,桥孔约束水流,桥下流速增大,使原来水流与河床泥沙相对平衡的运动状态遭受破坏,导致桥址断面发生一般冲刷和桥墩(台)近区的局部冲刷。在桥渡设计中,冲刷计算、孔径计算、建筑物布置以及综合方案的比较等都是以桥梁水力计算为工作基础的,而桥梁壅水计算是桥梁水力计算的主要内容之一。因此,对桥墩(台)产生的壅水高度做出科学、精确地计算分析,对桥梁设计和防汛工作都有一定的实际意义和应用价值[1-2]。
2、 桥梁壅水的计算
桥梁修建后,最大壅水高度△z一般发生在桥位上游断面处(有导流堤时在上游堤端附近,无导流堤时在桥位上游约一个桥孔长度处)。桥位断面的壅水高度△z’,一般可取1/2△z;对于山区和山前河流,洪水涨落急骤,历时短促,且河床质坚实不易冲刷时,可取△z;对于平原区洪水涨落很缓慢的河流,且河床质松软,易于造成一般冲刷时,桥下壅水可不计[3]。
桥梁壅水计算主要可以分为两类,即水面曲线法和简化公式法。水面曲线法以水动力学数学模型为基础,理论上较严密,但需要相关河道、桥梁较为详细的水文、地形等资料进行建模、率定和验证,对使用技术要求相对较高。
简化公式法计算所需资料较少,计算简便,较容易掌握应用。我国的桥梁设计规范中长期使用简化公式。桥梁壅水简化计算公式按照推导原理可以归纳为:以水流能量平衡原理为基础的能量型公式,以水流动量原理为基础的动量型公式,以堰流计算为基础的堰流公式,以及主要以试验资料为基础的经验公式。
本文主要采用水面曲线法和以堰流计算为基础的堰流公式进行桥梁壅水计算,对比分析。
方法一:水面曲线法
一维明渠非恒定流的基本方程为圣维南(Saint-Venant)方程组,通过瞬时流态法求解,整理可得能量方程,即伯努里(Bernoulli)方程:
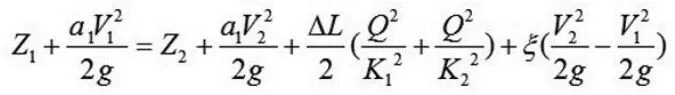
Z1、Z2——河道上、下断面的水位(m );
Q——河段设计流量(m3/s);
V1、V2——河道上、下断面的平均流速(m/s);
K1、K2——河道上、下断面流量模数(m3/s);
α——动能校正系数;
ξ——河段平均局部阻力系数;
L——上下断面间距(m);
g——重力加速度(m/s2)。
本文采用计算机编程的二等分迭代法进行河道水面曲线计算。基本思想:将解的存在区域,进行二等分,即分成两个子区域;判定解存在这两个子区域中的某一个子区域,然后对此子区域再进行二等分;……直至最后得到解。
在桥梁壅水计算中,同时考虑了糙率和局部阻力系数,可利用如下的能量方程:

式中:ξ系数选取是关键,对于方头墩一般取0.35;对于圆头墩,一般取0.18,且ξ取值时桥墩长宽比均应为4。v为紧接桥墩处的断面平均流速[4]。
方法二:宽顶堰堰流公式
宽顶堰堰流公式计算,即将河道过流断面概化为无坎宽顶堰来计算桥梁的壅水。计算公式如下:
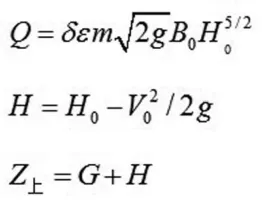
Q——过堰流量(m3/s);
H0——为计入行近流速水头的堰上水深(m);
δ——堰流淹没系数,取1.0;
g——重力加速度(m/s2);
m——堰流流量系数,应在0.32~0.385之间;
B0——总净过水宽度(m);
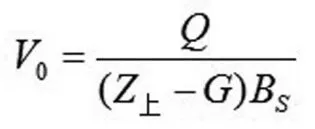
Z上——坝上水位(m);
G——河底平均高程(m);
BS——坝上水面宽度(m)。
3、实例应用
广州大桥桥位区位于梅城梅江反“S”型下部的弯道处(位置详见图1),水流与桥轴线的法线夹角约为12°。大桥桥位上游20m右岸处为七孔闸,下游约100m河道突然收缩,最窄处河床宽仅为160m。大桥桥位断面河床宽约320m,左岸(北岸)为淤积区,右岸(南岸)为冲刷区,桥位处河床南低北高,呈“V”字形,其左岸分布有浅滩,宽度约50m,滩面倾向河心,深槽偏向右岸,最深处可达10m以上,中泓位置大约距右岸堤防60~100m,河床最低标高为61.704m(珠基,后同)。

图1 广州大桥位置示意图
广州大桥主桥为(139m+106m)独塔单索面斜拉桥,主线桥引桥采用(3×30m)+(3×30m)和V(4×36.2m)+(2×30m)预应力连续箱梁。主塔墩位(Z8)位置距北岸较近,约106m,采用箱形截面,截面尺寸为15m(横向)×8m(纵向);主桥南侧边墩(Z7)距南堤75m,采用带扩大头板墩,迎水面墩宽为6.3m,两墩承台之间设立2.5m×1.8m的系梁。南侧引桥的两个桥墩(Z5、Z6),迎水面墩宽均为2.5m(参见图3)。河道范围内广州大桥桥墩立面示意图见图2。

图2 河道范围内广州大桥桥墩立面示意图
广州大桥的阻水比统计见表1。
根据“广东省河流糙率综合分析”成果,梅城河段的糙率值取为0.024。
本次以梅县(四)水文站设计的各频率水位作为起推水位向下游推算。采用梅县(四)水文站1945~2008年共有64年水位资料系列进行频率分析计算,得起推水位计算结果见表2。
采用伯努利方程,逐段试算推得大桥修建后的工程后水面线,与工程前现状水面线对比,得方法一计算的壅水值;根据宽顶堰堰流公式,得方法二计算的
4、结论
桥梁壅水计算中,水面曲线法以水动力学数学模型为基础,理论上较严密,但需要相关河道、桥梁较为详细的水文、地形等资料进行建模、率定和验证,对使用技术要求相对较高,对收缩区和扩散区的损失系数等要做若干假定。简化计算法公式推导时先要作出假定,往往根据实际掌握的试验资料和天然资料验证来确定系数或指数,具有经验或半经验性质。在实际工程应用中,需根据水文、地形资料的实际情况,对各计算方法的适用性进行分析,以便桥梁壅水计算更加符合实际情况。壅水值。计算成果见表3。
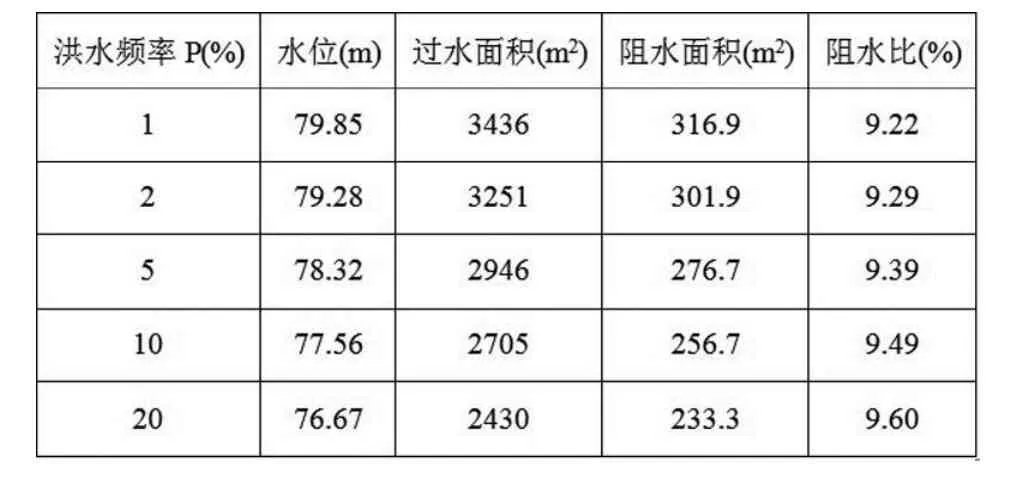
表1 广州大桥阻水比计算表

表2 广州大桥水面曲线法计算壅水的起推水位

表3 广州大桥壅水计算成果表
由上表可知,两种方法计算的结果基本上一致。综合两种方法,结合防洪需要采用较不利的情况作为计算成果,因此广州大桥的壅水计算采用堰流公式法的计算成果。
[1]陆浩. 桥梁壅水研究综述[J]. 铁道部科学研究院铁道建筑研究所
[2]曹瑞章. 桥前壅水的计算[J]. 铁道部科研院.铁道学报. 第8卷.1986.9
[3]TB10017—99.铁路工程水文勘测设计规范[S].
[4]李炜. 水力计算手册[M]. 武汉大学水利水电学院水力学流体力学教研室
[5]陈席珍,珠炳祥,黄必燑,蒋文娴. 桥前壅水的分析研究[J]. 铁道工程学报. 第4期.1990.1. P73-80
[6]梅州市广州大桥防洪评价研究报告.2009.10
10.3969/j.issn.1001-8972.2010.13.019

