马克思两部类模型非均衡增长分析及模拟

○刘坤 （浙江师范大学工商管理学院 浙江 金华 321004）

马克思两大部类模型揭示了部类经济均衡增长的重要意义。从数学上看，两部类平衡增长需要满足的条件是两部类增长速度g应该相等（g1=g）2。此处，g表示某一部类资本的增长速度，它等于该部类积累率与利润率之积，表示如下：g=θr=θ·。式中，θ为部类积累率，r为利润率，m'为剩余价值率，λ为资本有机构成（可变资本/不变资本的比率）。

一、两大部类商品交换表及其矩阵表示

在马克思扩大再生产的一个例子中，第一年年末总产品如下：

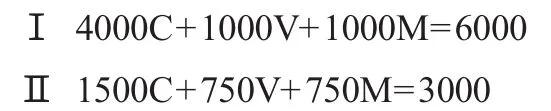
假设第Ⅰ部类（生产资料部类）有机构成λ1=4，第Ⅱ部类（生活资料部类）有机构成λ2=2，两大部类剩余价值率m'=100%，第Ⅰ部类积累率θ1=50%，第Ⅱ部类的积累率是20%。此时，第I部类的增长率为50%*1/5=10%，第Ⅱ部类的增长率为20%*1/3=1/15，约为6.67%；因此，第I部类增长速度超过了第Ⅱ部类，并不满足两大部类均衡条件；均衡条件下第Ⅱ部类积累率应当是30%。

在第一年年末（或第二年年初），上述年总产品分配情况如下。在扩大再生产的情况下，剩余价值分为两部分，其中一部分追加投资（这又分为追加不变资本和可变资本两部分），还有一部分用于资本家的消费，因此年末总产品分配如下：

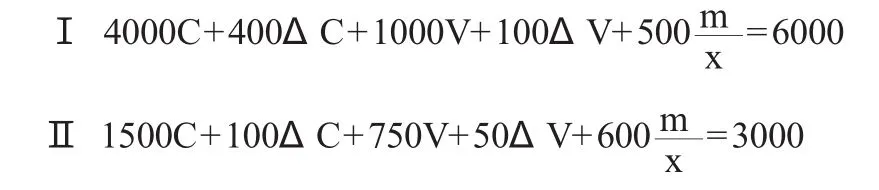
其中，第Ⅰ部类6000总产品中有4400是内部交换，而另外1600需要通过与第Ⅱ部类的商品进行交换；第Ⅱ部类3000产品中1400是在部类内部进行交换，而1600需要与第Ⅰ部类商品交换。

例如，e12表示第Ⅰ部类对第Ⅱ部类商品的需求，第Ⅱ部类对第Ⅰ部类商品的需求为e21。e11和e22分别表示了两大部类内部的商品需求。

再生产的均衡条件是部类间交换均衡：e12=e21。

在简单再生产条件下，第Ⅰ部类对第Ⅱ部类商品的需求为e12=（v+m）Ⅰ。第Ⅱ部类对第Ⅰ部类商品的需求为e21=cⅡ，因此均衡条件为：Ⅰ（V+M）=ⅡC。

在扩大再生产条件下，可以得到如下各元素：

e11=（c+Δc）Ⅰ=（1+g1）·cⅠ，其中 g1表示第 I部类增长率。

把各个具体数字代入，计算两大部类之间的相互需求如下：在第一年末。所以在第一年末两大部类进行交换的时候，市场是均衡的。

在第一年末对年总产品进行分配，用于下一年生产的某一部类可变资本和不变资本均比年初有所增长（增长率为g）：c'=（1+g）c，v'=（1+g）v。

按照上述分配进行生产到第二年末，年总产品为：

Ⅰ 4400C+1100V+1100M＝6600

Ⅱ 1600C+800V+800M＝3200

在第二年末，按照原有积累率扩大再生产的情况下，对上述年总产品进行分配如下：这时，两大部类之间交换的商品在价值上不相等，市场不能实现供需均衡。

二、两大部类之间需求不平衡的分析

1、价格波动

在商品市场上，由于第I部类增长快，供给相对过多，而第Ⅱ部类的增长慢，商品供给相对过少，在市场经济的作用下，其价格相应地下跌和上涨，价格波动很难预测。本文建立一个指标来近似地表示价格波动的程度。

两大部类价值不相等，因此只能是不等价交换。假设第Ⅱ部类商品价格逐渐上涨，最终价值1707的第Ⅱ部类商品与价值1760的第Ⅰ部类商品完成交换。

第Ⅱ部类商品价格由1707相应地上涨到1760。因此它的相对涨价幅度为，更准确地。其中，g为部类增长率，m'为剩余价值率（假设两部类相同），θ为积累率。.

下面对上式进行简化。先考虑p=0，没有通货膨胀的情况。我们已知道此时两大部类均衡增长，即g'2=g112。因此有：v1（1+g1+（1-θ1）m'）=cⅡ（1+g'2）=cⅡ（1+g1）。

本文中，g1=10%，g2=6.67%，因此p≈3.3%。相比于上面计算的3.1%，是个近似估计。

当然，在现实中，价格的波动可能会比较剧烈，因此大大超过上述的幅度。

2、商品存货的变化

三、两大部类经济非均衡增长的计算机模拟

在上述分析的基础上，本文利用EXCEL软件，对两大部类增长的情况进行了计算机模拟，得到在各种情况下两大部类的增长与波动。

表1 模拟的部分结果（积累率、增长率、存货和价格涨幅均为百分比）

在模拟中，本文假定两大部类根据上一期商品存货的情况来调整生产安排，当存货为正时，下调积累率从而降低了增长率；反之，当存货为负不够市场需求时，则增加积累率从而提高了增长率，用回归方程表示如下：

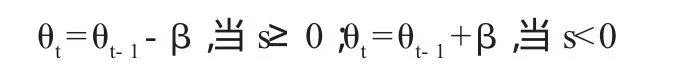
上式中，系数β为积累率的调整幅度。在本文中，第I和第Ⅱ部类积累率调整幅度分别为5%和2%。根据上述假定，我们可以知道部类增长率g=θr也呈现出自回归的特性：gt=gt-1-rβ。此式中r表示利润率，β为积累率的调整幅度，假设都是不变的。

通过模拟，发现经济增长存在着周期性的波动；存货率的波动与价格变化几乎是同步的（但是波动幅度相对要小），而滞后于两大部类增长率差异的变化（见图1、图2）。

图1存货率

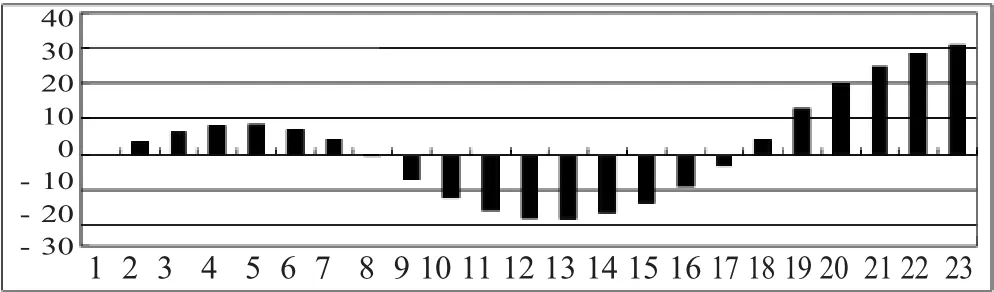
图2价格上涨指数

[1]马克思：资本论[M].北京：人民出版社，1976.

[2]张薰华、洪远朋：《资本论》提要[M].上海：人民出版社，1978.

[3]黄达：货币银行学[M].北京：中国人民大学出版社，1999.

[4]刘坤：马克思扩大再生产理论的数学解释[J].当代经济，2008（10）.