中小型物流企业建立共同配送合作条件的博弈分析

四川大学工商管理学院 郭彦玎

中小型物流企业建立共同配送合作条件的博弈分析

四川大学工商管理学院 郭彦玎

本文首先分析了共同配送的必要性,在了解博弈论中的相关理论背景的基础上,用完全信息下的无限重复动态博弈对单个配送企业在怎样的条件下建立配送联盟进行了初步讨论，使得这个合作联盟稳定可靠并且是经济有效的。

共同配送 完全信息 重复博弈

世界经济的发展使我国众多中小型物流企业面临着市场辐射小、运营效率低等诸多问题，及时改变我国现有物流企业的运作模式和经营方式成为当务之急，而实行共同配送正是一种应对危机的有效方法。通过共同配送，许多中小型物流企业能够实现规模经济效益，提高物流效率，优化资源配置，从而增强市场竞争力。然而，许多企业在联盟后产生的经济风险一直是实施共同配送的一个重要的障碍。

共同配送最早产生于日本，目前在国内外已经得到了迅速的发展。随着国内众多配送企业的成立，其争夺市场份额的局势愈演愈烈，我国配送企业面临着巨大的挑战，其大多呈现规模不大、一体化程度不高、配送资源较为零散、竞争力处于较低水平的现象。同时，国内配送企业各自运用相对分散的优势资源相互竞争，互相打压，造成配送资源的严重浪费，严重阻碍我国配送业的发展。

1 非合作博弈

非合作博弈亦称为负和博弈或零和博弈，是指一种参与者不可能达成具有约束力的协议的博弈类型，这是一种具有互不相容味道的情形。非合作博弈研究人们在利益相互影响的局势中如何选决策使自己的收益最大，即策略选择问题。在非合作博弈情况下达到的均衡成为非合作博弈均衡，也叫做纳什均衡。

在非合作博弈中，若每个局中人对其他局中人的策略集和支付函数都是知道的，且每个局中人也知道其他局中人知道自己对其他局中人策略集和支付函数都是知道的，即与博弈相关的一些信息是众所周知的，或者说相关信息是公共知识，这样的博弈成为完全信息下的博弈。在非合作博弈中，若每个局中人同时独立地采取自己的策略，或行动时间有先后顺序与同时行动的结果是相同的，并且只进行一次，这样的博弈称为静态博弈，又称为一次博弈。在一些情况下，只有一次博弈但是信息是不对称的，这种情况下的博弈叫做不完全信息下的静态博弈。

然而，在现实的经济生活和社会生活中，这样简单的博弈实在太少了，因为在博弈过程中，局中人采取行动也不一定是同时的，因此，又产生了完全信息下的动态博弈和不完全信息下的动态博弈。

2 重复博弈

一个基本的静态或者动态博弈重复进行多次，可以是有限的，也可以是无限的，这样的博弈就是重复博弈，有限次的重复称为有限重复博弈，无限次的重复称为无限重复博弈。其中的每次博弈称为“阶段博弈”。重复博弈是动态博弈中的重要内容，它可以是完全信息的重复博弈，也可以是不完全信息的重复博弈。 重复博弈是指同样结构的博弈重复许多次。当博弈只进行一次时，每个参与人都只关心一次性的支付；如果博弈是重复多次的，参与人可能会为了长远利益而牺牲眼前的利益，从而选择不同的均衡策略。因此，重复博弈的次数会影响到博弈均衡的结果。

在重复博弈中，每次博弈的条件、规则和内容都是相同的，但由于有一个长期利益的存在，因此各博弈方在当前阶段的博弈中要考虑到不能引起其他博弈方在后面阶段的对抗、报复或恶性竞争，即不能像在一次性静态博弈中那样毫不顾及其他博弈方的利益。有时，一方做出一种合作的姿态，可能使其他博弈方在今后阶段采取合作的态度，从而实现共同的长期利益。

影响重复博弈均衡结果的主要因素是博弈重复的次数和信息的完备性。在重复博弈中，参与人存在着短期利益和长远利益的均衡，有可能为了长远利益牺牲短期利益而选择不同的均衡策略。重复博弈的这个结果，为现实中的许多合作行为和社会规范提供了解释。信息的完备性之所以影响均衡结果，是因为如果每一个参与人的特征不为其他参与人所知时，该参与人就很有可能积极建立一个好声誉，以换取长远利益。重复博弈具有三个基本特征：(1)重复博弈的阶段，博弈之间没有“物质”上的联系，即前一个阶段博弈并不改变后一个阶段的博弈的结构；(2)在重复博弈的每一个阶段，所有参与人都观测到该博弈过去的历史；(3)参与人的总收益是所有阶段博弈的收益的贴现值之和或加权平均数。

本文是针对收益函数矩阵，用将完全信息的静态博弈方法与完全信息下的无限重复动态博弈相结合的方法对共同配送的建立条件进行了讨论。

3 共同配送企业合作条件的重复博弈分析

3.1 模型假设

(1)参与人：本文的模型中有两个参与人：一为单个配送企业X;另一个为单个配送企业Y。

(2)策略集：本文的模型中两企业可以选择的策略有两个：合作或者不合作(企业的合作与不合作，是指建立不建立共同配送联盟)。则企业X与企业Y的可选择策略集合都为{不合作，合作}。

(3)支付函数Q：本文模型中，假设企业双方的收益如下表所示：

3.2 模型分析

本文的模型中将单个配送企业X和Y进行合作的策略选择过程假设为一个重复博弈过程。假设两个企业都是具有行为理性的，并且都是具有追求既得利益的经济理性的，同时各自不仅知道自己每个行为后的收益，也完全知道对方的收益及相应的策略步骤，即模型中参与企业的信息是完全信息的。

两个配送企业合作后的收益大于两个企业都选择不合作时的收益，而两方合作后，其中任何一方采取背叛行为(不合作)，则背叛的一方获得比采取合作行为企业的一方获得较大的收益，因为背叛的一方不能获得比合作时的更多的收益就不会选择不合作，而采取合作行为的一方由于对方的不合作遭受损失， 即满足条件T＞R＞P＞S。

在采用触发策略的情况下，开始时两企业的体理性使双方先试图合作，两方企业都对对方采取合作的行为，但是其中任何一个企业对对方采用了不合作的策略，在今后发展的所有时期内，另一企业也会相应采取背叛行为。

在这种状况下，如果所有参加配送联盟的配送企业在联盟整个期间都采取合作行为，在整个联盟期间单个配送企业的期望收益为：

(0＜θ＜1，θ=1/(1+r)，θ为贴现因子，r为贴现利率)

如果在某一阶段其中一个企业背叛，其他的配送企业对其采取报复行为，那么在报复行为下，其所得的收益为：

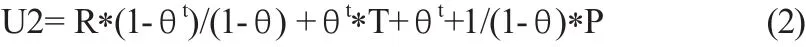
因此，如若要单个配送企业S采取合作策略，则必须使单个配送企业S采取合作策略的全部收益大于其采取不合作策略情况下的全部收益：

对不等式进行整理，可推出：

此时双方都达到最大的收益，实现“帕累托最优”。因此，单个配送企在此时的条件下能够等到稳定的共同配送联盟，并且此时的收益为最大，实现经济有效性，降低经济风险。

4 结语

本文运用完全信息下的无限重复动态博弈的观点，分析了各个单个配送企业的合作条件，根据分析结果可知，单个配送企业在寻找合作伙伴时，需要对其他单个配送企业在单独工作情况下的收益和在合作情况下的收益进行评估(既是尽可能的实现完全信息)，并密切关注贴现利率的变动，在小于θ时，这时的出发策略就可能使得联盟里的企业采取有利于短期利益的行为，导致共同配送联盟的破裂。在大于θ基础上建立的共同配送，在其系统内，做到高效的服务，满足越来越个性化的顾客需求，而且这样的共同配送联盟是经济有效并且稳定的，这样的联盟在市场的竞争中才有较强的竞争力，才能争取获得更大的市场份额。

[1]汪贤裕,肖玉明.博弈论及其应用[M].北京:科学出版社,2008.

[2]刘永礼.对物流企业战略联盟的博弈分析[J].科技信息,2008,(34).

[3]彭本红.基于博弈理论的第三方物流合作伙伴关系研究[M].北京:经济科学出版社,2008.

[4]张麦玲.物流企业战略联盟的博弈分析[J].经营管理,2008.

[5]涂燕,王丽,罗琳.第三方物流企业合作条件的博弈分析[J].经济纵论,2009.

F252

A

1005-5800(2010)10(c)-128-02