壳单元在压力容器分析设计中的应用

陈小辉，董俊华，高炳军

（河北工业大学 化工学院，天津 300130）

0 引言

随着计算机辅助设计技术的飞速发展，有限元法越来越多地应用于压力容器的分析设计中．然而在建立有限元模型时，对于需做整体分析的大型设备如固定管板换热器，如果全部使用实体单元建模，计算规模将相当庞大．虽然可采用子模型法解决此类问题[1]，但子模型法需进行二次计算，且计算过程复杂．为了降低计算费用并得到可靠的计算结果，利用壳单元代替实体单元对包括总体结构不连续区在内的部分结构进行建模，仅对局部结构不连续区利用实体单元建模无疑是一种可选方案，这样做可以在有限计算资源下同时得到总体结构不连续区及局部结构不连续区的较为准确的计算结果．虽然ASMEⅧ-2[2]指出基于板壳理论的壳单元的计算结果可直接用作薄膜应力及弯曲应力，然而这样做与按实体单元计算并进行线性化处理得到的结果是否具有可比性，或者说利用壳单元的计算结果进行应力强度评定是否可靠，仍是一个值得讨论的问题．壳单元在结构应力分析中应用广泛[3-4]，但在压力容器分析设计中应用较少，仅有为数不多的几篇文献 [5-8]对此进行了初步探讨．笔者以斜锥壳为例，分别建立壳单元及实体单元有限元计算模型，比较按两种不同方法计算得到的用于强度评定的应力强度或相当应力，对使用壳单元进行压力容器的分析设计的可行性进行探讨．

1 壳单元及实体单元计算结果的应力线性化过程

1.1 壳单元计算结果的应力线性化过程

基于板壳理论的壳单元可以输出节点在外表面、内表面和中面的各向应力分量，可按照式 (1)~式 (2)计算薄膜应力和弯曲应力．

据此可直接计算评定位置的薄膜应力以及内外壁的薄膜加弯曲应力的应力强度或相当应力．

1.2 实体单元计算结果的应力线性化过程

通常，分析设计采用有限元法对高应力区进行计算时，需要用实体单元建模，且沿壁厚方向至少划分4个单元（对于线性单元），并沿应力评定路径做插值计算，根据插值点的各向应力分量按合力等效原则进行均匀化处理，按净力矩等效原则进行线性化处理，从而得出该路径的薄膜应力分量、线性应力分量及峰值应力分量，然后计算相应的应力强度，并根据其结构及载荷特点进行应力分类．

ASMEVIII-2（2007版）在实体单元应力线性化过程中指出，线性应力中一般不再计入剪应力，除非是由于扭转造成的线性分布的剪应力，这是因为横向力引起的剪应力沿壳体厚度一般为抛物线分布，中性层位置最大，内外壁处为零[9]．其中用于计算的各个应力分量是在局部坐标系下获得的．因此，应力处理线上薄膜应力张量计算时仍需考虑各个应力分量，即

而应力处理线上线性分布的应力张量按上述原则不再计入剪应力．

据此可计算应力处理线上薄膜应力以及内外壁的薄膜加弯曲应力的应力强度或相当应力．

应当指出的是ASMEVIII-2（2007版）采用最大畸变能理论 (MISES)代替最大剪应力理论 (TRSECA)来计算用于强度评定的相当应力，由于目前我国标准JB4732-1995（2005确认版）仍采用根据最大剪应力理论(TRSECA)得到应力强度进行强度评定，以下讨论中同时计算了应力强度(TRSECA)及相当应力（MISES），应力处理线上线性应力的计算分别考虑了计入与不计入剪应力两种情况．

2 算例——斜锥过渡区的应力分析

以斜锥过渡区的应力分析[10]为例，分别建立壳单元及实体单元有限元计算模型，比较按两种不同方法计算得到的用于强度评定的应力强度或相当应力，并进行分析讨论．

某斜壳锥及与其连接的筒体材料为Q345R，设计应力强度为173MPa，弹性模量E=2×105MPa，泊松比=0.3．小端筒体内径=1000mm，大端内径为=2000mm，斜锥小端过渡区转角半径=100mm，斜锥大端过渡区转角半径=200mm，偏锥角=60°，斜锥、大小端筒体壁厚 =12mm，管板壁厚=60mm．小端筒体长度=130mm，大端筒体长度=500mm，内压=0.58MPa．斜锥壳过渡区结构及力学模型如图1所示．

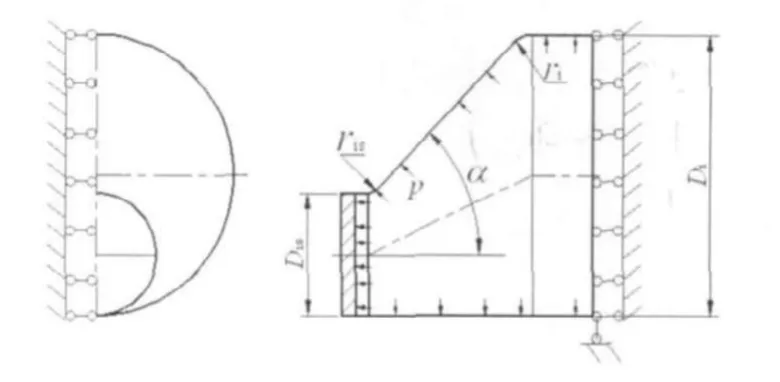
图1 斜锥壳过渡区的结构简图Fig.1 Sketch of knuckle regions in slant conical shell

2.1 有限元模型

2.1.1 壳单元模型

采用ANSYS的SHELL63壳单元建模，如果平面单元没有超过15度的弧度，那么这些平面单元的组合可以很好的模拟曲面．取结构的1/2建立有限元模型，其中纵剖面施加对称约束，大端筒体横截面约束轴向位移，内表面施加内压．大端筒体长度值远大于边缘应力的衰减长度．壳单元模型如图2所示，共划分2 840个单元．

2.1.2 实体单元模型

选用ANSYS的solid45单元建立三维实体结构模型．取结构的1/2建立有限元模型，其中纵剖面施加对称约束，大端筒体横截面约束轴向位移，内表面施加内压．大端筒体长度值远大于边缘应力的衰减长度．实体单元有限元模型如图3所示，共划分13 256个单元，厚度方向剖分4份．

图2 斜锥壳单元有限元模型Fig.2 Shell finite element model of the slant conical shell

图3 斜锥实体有限元模型Fig.3 Solid finite element model of the slant conical shell

2.2 有限元计算结果

基于壳单元的斜锥过渡区有限元计算结果如图4所示，基于实体单元的斜锥过渡区有限元计算结果如图5所示．两种单元类型的计算资源占用及计算精度对比情况见表1．由表1可见稀疏矩阵求解所需内存、硬盘空间消耗以及运行时间壳单元均明显低于实体单元，而两者的能量百分比误差相差却不大，即两者具有相当的计算精度．

图4 斜锥壳单元模型MISES相当应力云图Fig.4 The MISES equivalent stress contour of slant conical by shell element

图5 斜锥实体单元模型MISES相当应力云图Fig.5 The MISES equivalent stress contour of slant conical by solid element model

表1 占用计算资源比较Tab.1 Comparison of occupation of computing resources

由图4与图5可见，壳单元模型与实体单元模型的计算结果十分接近，最大MISES相当应力的位置均位于斜锥大端过渡区内壁，大小相差无几．

2.3 应力分类结果的比较

对于上述算例，通过最大MISES相当应力点沿壳体的法线方向设定应力处理线，分别按前述方法进行处理，得到处理线上薄膜应力强度（或相当应力）以及薄膜加弯曲应力强度（或相当应力），计算结果列于表2．

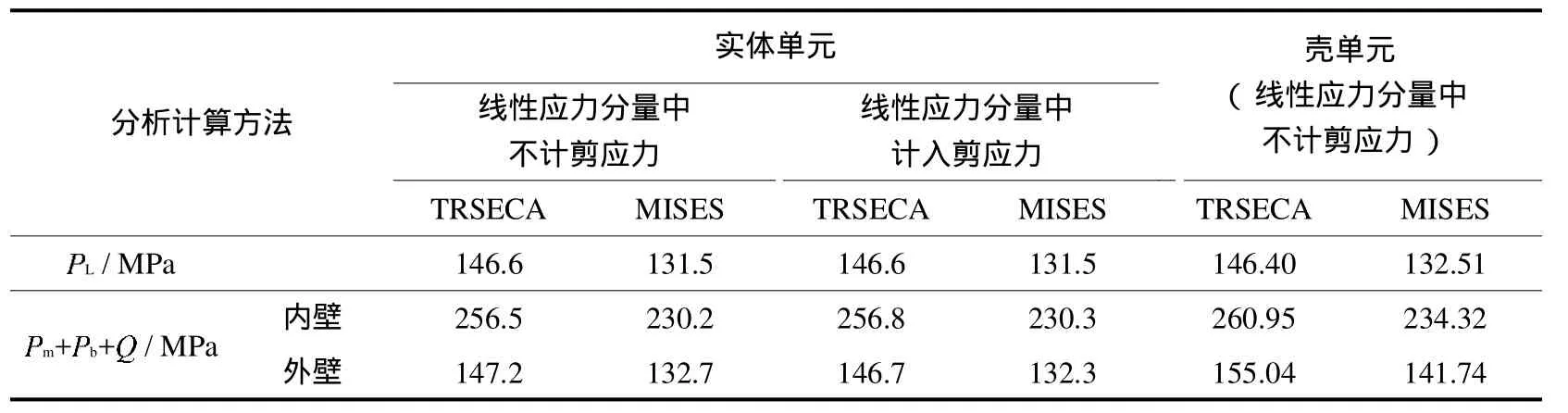
表2 应力分类结果比较Tab.2 Comparison of stress classification

由表2可看出，对于本算例，线性应力分量中是否计入剪应力对实体单元计算结果影响不大，这与本算例中实际结构的剪应力较小有关．观察所有的计算数据，对于本算例，MISES相当应力值均小于TRESCA应力强度值．可见采用第四强度理论的计算结果比第三强度理论值小，说明第三强度理论偏于保守．与实体单元计算结果相比，按壳单元计算时，结构的局部薄膜应力相差不大，而薄膜加弯曲应力值均稍偏大．

利用APDL(ANSYS Parametric Design Language)语言开发了该结构的参数化有限元计算模型，并对一系列结构尺寸的斜锥壳进行了分析计算．设定为 1.5、2.0、2.5，=30°~60°，==0.1，进行比较，图6给出了结构最大相当应力点位置壳单元与体单元的应力线性化处理结果（采用MISES相当应力）．对于此结构，在所计算的参数范围内，无论是局部薄膜应力，还是薄膜加弯曲应力，壳单元模型的计算结果均稍偏大，局部薄膜应力最多偏大3.2%，薄膜加弯曲应力最多偏大9.14%．可见，在大规模工程计算中用壳单元进行有限元计算稍显保守，用它来代替实体单元是可行的．

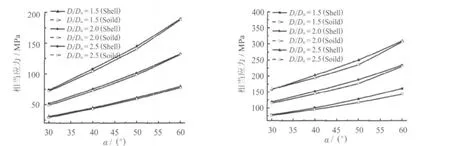
图6 壳单元与实体单元在不同结构参数下的相当应力的比较Fig.6 Equivalent stress comparison of shell element and solid element under different structural parameters

3 结束语

通过对等厚度斜锥壳过渡区结构的参数化有限元应力分析发现，壳单元的计算结果与实体单元计算结果相比，无论是局部薄膜应力还是薄膜加弯曲应力的相当应力均稍偏大，其中局部薄膜应力的相当应力最大偏差为3.2%，薄膜加弯曲应力的相当应力最大偏差为9.14%．而总应力的相当应力相差无几．从分析设计的观点看，因壳单元计算结果稍显保守，在涉及此类压力容器总体结构不连续区的大规模有限元计算中采用壳单元是可行的．这样可对包括此类总体结构不连续区在内的大部分区域采用壳单元建模，仅对局部结构不连续区采用实体单元建模，从而利用有限的计算资源同时实现不同区域的应力计算，且保证足够的计算精度．

[1]高炳军，高艳红，李金红．子模型在球罐应力分析中的应用 [J]．压力容器，2009，26（5）：27-31．

[2]ASMEBoiler&Pressure Vessel Code, Ⅷ Division2 Alternative Rules,Rulesfor Construction of Pressure Vessels[S]．2007．

[3]李霄，吉玲康，赵文祯，等．高钢级管线管压缩变形能力研究 [J]．机械强度，2009，31（1）：155-159．

[4]谢元丕，冯刚．ANSYS三维实体单元与板壳单元的组合建模研究 [J]．机械设计，2009，26（4）：5-7．

[5]Michael A Porter，Dennis H Martens，Caldwell SM．A suggested shell/plate finite element nozzle model evaluation procedure[J]．ASME Journal of Pressure Vessel Technology，2008，130（3）：031202-1~031202-6．

[6]Koves WJ，Nair S．A finite element for the analysis of shell intersection[J]．ASME Journal of Pressure Vessel Technology，1996，118（4）：339-406．

[7]郭崇志，陈文昕，纪昌盛．大型薄壁压力容器Shell单元模型的应力线性化分析 [J]．化工机械，2005，32（5）：275-278．

[8]曹占飞．用壳单元进行30°斜开孔补强计算的可行性研究 [J]．石油化工设备技术，2007，28（3）：1-2．

[9]陆明万，徐鸿．分析设计中若干重要问题讨论（二)[J]．压力容器，2006，23（2）：28-32．

[10]高炳军，王洪海，程伟，等．固定管束釜式重沸器斜锥转角过渡区应力分析 [J]．力学与实践，2008，37（1）：39-42．