多源点物流配送车辆调度模型探讨

覃运梅 （广西工学院，广西 柳州 545006）

多源点物流配送车辆调度模型探讨

覃运梅 （广西工学院，广西 柳州 545006）

根据问题的复杂性，考虑车辆条件的约束，建立了以总费用最小为目标的数学模型，并根据模型的特点设计出相应的启发式算法，使问题在合理的时间内得出由多个配送中心为所有需求点配送货物的车辆分派方案。实例证明，该模型符合实际问题，算法合理，具有实际应用价值。

多源点；物流配送；模型；启发式算法

0 引 言

物流配送优化主要是对配送车辆调度的优化问题[1]，它是一个复杂的组合优化问题，需要考虑多种约束、多个目标，属于NP难题[1-4]。车辆调度问题又可以分为单源点调度问题和多源点调度问题。单源点调度问题是指只从一个货源点调度车辆为多个需求点配送货物，多源点调度问题则是指从多个货源点调度车辆为多个需求点配送货物。前不久，作者对单源点配送车辆调度问题进行了研究，建立了双目标模型，并把问题分成2阶段进行求解，第1阶段用改进的动态聚类算法分派车辆的配送任务，第2阶段用动态规划方法求出车辆的行车路线[5]，取得了很好的效果。

本文在文献[5]的研究基础上，进一步对多源点调度问题进行研究，把问题描述为数学模型，并根据模型的特点设计了相应的启发式算法进行求解。

1 建立模型

1.1 问题假设

（1）各个配送中心的货物供应量充足；

（2）没有特殊装载要求的货物，即所有的货物都可以混装在一起；

（3）对于装载的货物，仅考虑体积和重量的限制；

（4）车辆的容积和额定载重量都相同，各个配送中心的车辆数有限，总的车辆数充足；

（5）对于满足整车运输的需求点，优先从最近的配送中心直接派车，故文中模型假设每个需求点的货物都不够装满一整车。

1.2 变量定义

将模型中所涉及的变量定义如下：

M——表示可用车辆总数 （模型中假设车辆数M足够用）

Ml——表示配送中心l可供调度的车辆数

L——表示配送中心个数

N——表示网络结点数，即配送中心及需求点数的总和，需求点有N-L个 （1个需求点所需的货物视为1件，即总的货物件数为N-L）

dij——表示从i到j的距离 （当i,j=1,2,…,L时表示物流中心，当i,j=L+1,L+2,…,N时表示需求点）

V——表示车辆额定容积

W——表示车辆额定载重

Vj——表示需求点j所需货物的体积

Wj——表示需求点j所需货物的重量

C0——表示指派一辆车的固定费用

C1——表示车辆行驶的每公里运输单价

1.3 模型建立

建立配送车辆调度的数学模型如下：

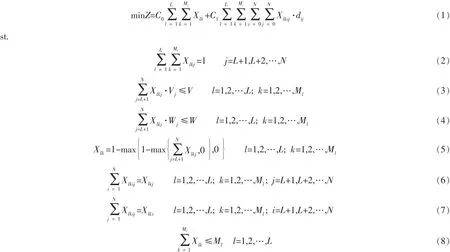
在上述模型中，式 （1）表示求最少的运输费用；式 （2）表示每个需求点只由一辆车配送；式 （3）表示每辆车装货不超过其额定容积；式 （4）表示每辆车装货不超过其额定载重；式 （5）表示若＞0， 则Xlk=1， 即如果配送中心l的车辆k为需求点j配送货物，则该车辆执行运输任务，此时目标函数需计算指派该车的固定费用；式 （6）表示指派的车辆只驶入所送货的需求点；式 （7）表示指派的车辆只驶出所送货的需求点；式 （8）表示每个配送中心指派的车辆数不超过其可调度的车辆总数。

2 模型求解

上述模型属于复杂的数学难题，为在合理的时间内得到满意解，本文根据模型特点提出了一种启发式算法，算法描述如下：

步骤1 计算每个需求点与各个配送中心的距离，按照就近原则进行归类分群，即把各个需求点归入与之距离最近的配送中心。判断各个群内所有需求点所需货物的总体积是否超过所有车辆的总容积，或者需求点所需货物的总重量是否超过所有车辆的总容重，若是，则记该群为超饱和群。

步骤2 考虑未分派车辆的所有配送中心，计算其地理位置重心，若存在超饱和群，则优先对超饱和群内分派车辆执行配送任务；否则对与该重心距离最远的配送中心所对应的群分派车辆执行配送任务。

步骤3 从该群内与重心距离最远的需求点开始，以该需求点为中心，添加相邻的需求点，直至达到一辆车的体积、重量的最大容量，把这些需求点分派给同一辆车；同样的方法分配该群内的其它需求点。若该群内的所有需求点均分配完毕且满足所分派车辆的体积、重量的约束，转入步骤5，否则，转入步骤4。

步骤4 把剩下的需求点归入与之距离最近的未分派车辆的需求点所在的群，返回步骤2和步骤3，直至所有的群都分派车辆完毕。转到步骤5。

步骤5 对每一辆车分派到的需求点，用Dijkstra算法[6]求出该车的最短行驶路线。

3 算 例

3.1 算例描述

有3个物流配送中心向25个需求点配送货物，车辆的额定载重量为9t，额定容积为20m3，指派一辆车的固定费用C0为30元，车辆行驶的每公里运输单价C1为2元/公里，各个配送中心及需求点的坐标、配送中心的车辆数、需求点的坐标所需货物的体积及重量如表1所示，试制定一个合理的运输方案，使总的运输费用最少。

表1 基本信息表

3.2 算例求解

步骤 （1） 按照步骤1的方法，归入配送中心1的需求点有 { 4,5,6,7,8,9,10,17,21,22 } ；归入配送中心2的需求点有 { 11,12,13,14,15,20,25 } ；归入配送中心3的需求点有 { 16,18,19,23,24,26,27,28 } 。其中配送中心1对应的群为超饱和群。

步骤 （2） 计算未分派车辆的配送中心1、2、3的重心坐标得到 ( 27 , 23 ) ，配送中心1对应的群为超饱和群，因此优先考虑对配送中心1分派车辆。

步骤 （3） 计 算配送中心1对应的各需求点与重心坐标 ( 27 , 2 3 ) 的距离为{27.8,22,15,9.85,14.9,18,22.4,8.54,20.9,15.2}，最大者为27.8，即以需求点4为中心，添加相邻的需求点。该群内与需求点4的距离为{0,6.71,18.4,19.7,23.4,23,12.4,23.1,16.3 } ，按照从小到大排序的对应需求点为 { 4.5,10,22.6,7,17,9,21,8 } ，需求点4的重量、体积集合为 { W ,V }={3. 1 ,6 . 8}，依次添加需求点5后 { W ,V } ={5. 1 ,1 0 .3}，添加需求点10后 { W ,V }={8. 2 ,1 4.9}，添加需求点22后 { W ,V }={10 . 6 , 21 } ，此时重量、体积均超过车辆的额定值，故需求点22不能分派给该车辆。该车辆记为X11，所以得到车辆X11分派的需求点为 { 4, 5 ,1 0 } ，对该群内剩下的需求点 { 6,7,8,9,17,21,22}用同样的方法分派车辆，得到车辆X12分派的需求点为 { 6, 8 ,2 1 }，X13分派的需求点为 { 7, 9 ,2 2 } 。此时，配送中心1的车辆已经分派完毕，但还有需求点 { 17 } 未分派到车辆，故转入 （4）。

步骤 （4） 把剩下的需求点 { 17}归入与之距离最近的未分派车辆的需求点所在的群。计算需求点 { 17}与未分派车辆的需求点{11,12,13,14,15,16,18,19,20,23,24,25,26,27,28}的距离为{18.9,17.3,13.3,23.3,31.3,24.6,29.1,8.06,32.5,31,14.2,28.6,21.5,13.6,12.1}，最小为8.06，对应需求点 { 19}，故把需求点 { 17}归入需求点 { 19}对应的配送中心3所在的群。 转到步骤 （2）。

用同样的方法得到配送中心2的车辆X21分派的需求点为 { 12,14,25 }，车辆X22分派的需求点为 { 11 , 13 } ，车辆X23分派的需求点为 { 15 , 20 } ；配送中心3的车辆X31分派的需求点为 { 17,19,24,27,28 } ，车辆X32分派的需求点为{16,18,23,26 } 。所有的群都已经分派车辆完毕，转到步骤 （5）。

步骤 （5） 用Dijkstra算法求出每一辆配送车辆的最短行驶路线。

按照以上步骤得到优化方案见表2。

表2 车辆调度优化方案

4 结束语

本文的研究成果可以为物流配送调度人员提供依据，从而实现物流科学化，对物流企业降低物流成本、提高服务质量、增加经济效益有显著意义。

[1] 张之富.物流配送车辆优化调度研究[D].上海：上海海事大学 （硕士学位论文），2007.

[2] L.Cooper.Location-Allocation Problem[J].Operations Research，2006,11(3):331-343.

[3] 郑称德，黄达.客户需求驱动的多层物流网络选址规划模型与算法[J].系统管理学报，2009(2):232-236.

[4] 程赐胜，蒲云虎，吴颖.集成化物流选址—路径问题优化模型的算法研究[J].中南林业科技大学学报 （自然科学版），2008,28(5):113-118.

[5] 覃运梅，王玲玲，郝忠娜.基于改进的动态聚类算法的配送车辆调度研究[J].合肥工业大学学报 （自然科学版），2009,32(7):962-965.

[6] 胡运权.运筹学教程[M].3版.北京：清华大学出版社，2007:250-253.

Research on Vehicle Scheduling Model of Multi-source-point Distribution

QIN Yun-mei (Guangxi University of Technology,Liuzhou 545006,China)

According to complexity of the problem,considering the constraint condition of vehicles,the optimal model with the minimization of total cost as the object was established,and the corresponding heuristic algorithm was put forward to solve the model.So the vehicle assignment scheme for delivering goods from numbers of distribution center to all of demand points could obtained in acceptable time.The practical application shows that the model in line with the practical problems and the algorithm is appropriate.Both model and algorithm are of practical value.

multi-source-point;logistics distribution;model;heuristic algorithm

F224

A

1002-3100(2010)09-0032-04

2010-07-23

广西工学院青年基金项目，项目编号：院科社1074205。

覃运梅（1976－），女，广西贵港人，广西工学院汽车工程系，讲师，硕士，研究方向：物流系统优化与管理。