层状介质上双频激电的电磁耦合效应

王顺国,熊 彬

(中南大学 信息物理工程学院,湖南长沙 410083)

层状介质上双频激电的电磁耦合效应

王顺国,熊 彬

(中南大学 信息物理工程学院,湖南长沙 410083)

从电偶极子谐变电磁场的基本公式出发,研究了层状介质上双频激电的电磁耦合特点。经研究表明,用中梯、偶极装置观测层状介质,电磁耦合随任意层电阻率值变大而减小;随低阻层的相对变薄而变小;随收发距的减小而减小。此外,用中梯测量时,电磁耦合在AB(供电极距)中部最强,远离中部时耦合效应会逐渐减小;且供电极距越小、离主测线越远,电磁耦合也越小。而用偶极测量时,供电极距的变化对电磁耦合的影响比中梯小。

双频激电;电磁耦合效应;层状介质

0 前言

随着激发极化法的不断发展,电磁耦合这一问题越来越受到地球物理勘探工作者的重视。在电磁测深中,电磁耦合含有一定地下介质的电学信息,是电磁测深中的有用信号,但电磁耦合在双频激电测量中是一种很强的干扰因素,尤其在低阻覆盖区和大极距测量时,严重影响了勘测深度与精度,从而阻碍了激电法的推广[1]。为解决这一问题,对电磁耦合效应进行研究是有必要的。

二十世纪中期,国外开始深入研究激电测量中的电磁耦合效应,并得到很多可贵结论。例如:M illett[2]公布了在均匀半空间表面上,偶极装置测量时实用电磁耦合计算对照表;Sunde[3]推导了水平层状大地表面上接地导线间电磁耦合的理论解;W ynn等[4]改进了低阻覆盖区的激发极化勘探技术,并提出了一种去耦的方法;Dey等[5]详细论述了二层介质在频率域和时间域偶极、三级装置的电磁耦合情况;Hohm ann[6]依据偶极装置,计算出了二层模型的电磁耦合;Zonge[7]提出高频激电效应弱而电磁效应强,低频则反之,据此可以利用多频测量进行校正;Pelton[8]将感应耦合近似看作C=1的Cole-Co le模型,从观测的总响应中去掉,以达到校正的目的。在国内,战克等[9]对变频法中电磁耦合规律进行了分析,并提出了校正方法;何继善等[10]从电磁耦合的时域特性着手,提出利用时间特性分离并克服电磁耦合的方法;熊彬等[11]针对均匀半空间,研究了中梯测量时二种布线方式的电磁耦合效应。作者在本文从电偶极子谐变电磁场的基本公式出发,用Fortran语言进行了中梯、偶极装置下多种模型的电磁耦合计算。

1 基本理论

图1及下页图2分别表示中梯、偶极装置示意图。AB是供电电极,ab是测量电极。发送电极和接收电极间的阻抗可以表示为式(1)[12]。

图1 中梯装置Fig.1 Central gradient array

在式(1)中:

σj(ω)=σ′j(ω)+iσ″j(ω),为第j层频率为ω的复电导率,当ω=0时,有σj(0)=σ′j(0)。

对于最底层,存在Fm(g)=Lm(g)=1.0,作者在文中取m=2。

由于文中θ=0,所以公式(1)可以简化为

可以利用阻抗的模,也可以利用相位计算视频散率,作者选用模对电磁耦合效应进行分析,有

其中 f0表示低频;f1表示高频。

为了便于解释,作者在文中用相同的频率(低频f0=1/13 Hz,高频f1=1 Hz)和二层模型进行研究,上层介质的电阻率为ρ1,层厚为h1;下层介质的电阻率为ρ2。

2 中梯装置

2.1 电阻率对电磁耦合的影响

取h1=200 m、AB=1 km、ab=50 m、ρ2=100Ωm、ρ1从10 000Ωm到10Ωm以10为倍数逐减。从图3可以看出,当ρ2不变,而ρ1由小变大时,电磁耦合效应逐渐减小,且图3中表明在中间位置,电磁耦合效应最强;远离中部时电磁耦合效应会逐渐减小。反之,ρ1不变,ρ2由小变大时电磁耦合效应也减小。为

图3 F s随第一层介质电阻率变化的剖面图Fig.3 Curvesof F sw ith the changesof resistivity to first layer

2.2 层厚对电磁耦合的影响

取AB、ab同上,ρ1=10Ωm、ρ2=100Ωm,h1从200m到500m以100m间距逐增。从图4(见下页)可以看出,上层为低阻介质时,随层厚的加大,电磁耦合效应增强;反之,上层为高阻介质时,随层厚的加大,电磁耦合效应减弱。由此可知,当层厚变化时,电磁耦合效应随低阻层的相对变薄而变小。

2.3 供电极距AB变化对电磁耦合的影响

取h1=200m,对ρ1=100Ωm、ρ2=1 000Ωm的模型,极距AB从1 000m到1 300 m以100m间距逐增。从图5中可以得出结论:电磁耦合效应随极距AB的增大而明显增大。对ρ1>ρ2的模型,可以得到相同的结论。

图4 F s随第一层介质厚度变化的剖面图Fig.4 Curvesof F sw ith the changesof thickness in the first layer

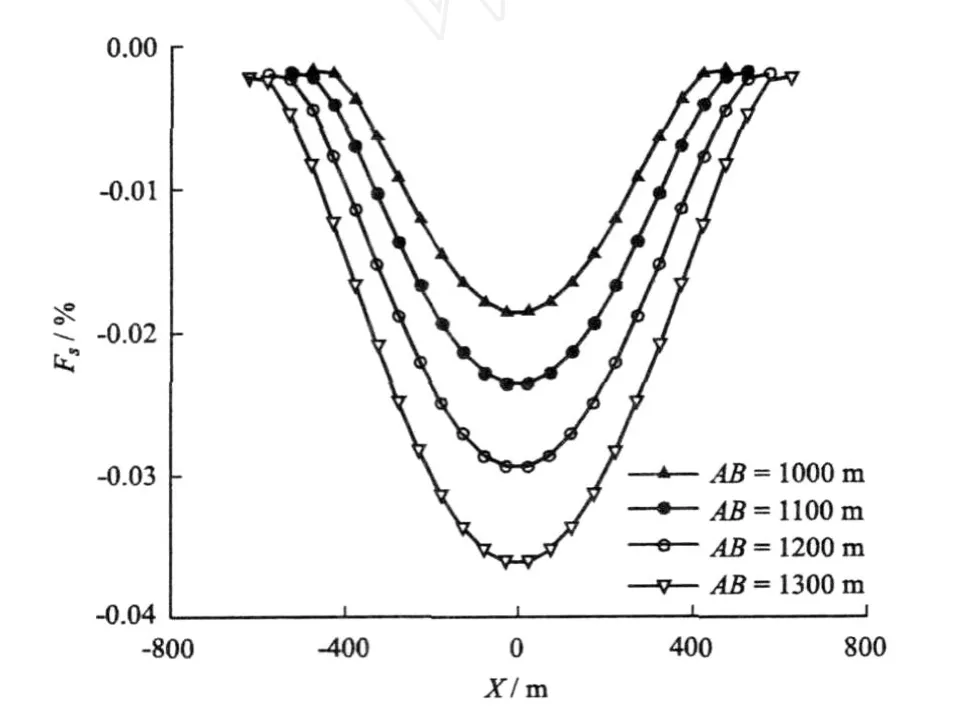
图5 F s随极距AB变化的剖面图Fig.5 Curvesof F sw ith the changesof power-supp ly po lar distance

2.4 AB与ab间距d y对电磁耦合的影响

取h1同上,对ρ1=100Ωm、ρ2=1 000Ωm的模型,AB与ab间距d y以20 m、30 m、40 m、50m变化。从图6看出,随间距d y的增大,电磁耦合效应减小。对ρ1>ρ2的模型,可以得到相同的结论。

3 偶极装置

3.1 电阻率对电磁耦合的影响

图6 F s随AB与ab间距d y变化的剖面图Fig.6 Curves of F sw ith the changes of parallel distance between AB and ab

取L=100m(如图2,为供电极距),N=1、2、…、18(为间隔系数),h1=200m,ρ2=100Ωm,使得ρ1从10 000Ωm到10Ωm以10为倍数逐减。从图7看出,ρ2不变,ρ1由小变大时电磁耦合效应减小;反之,ρ1不变,ρ2由小变大时电磁耦合效应也减小。并且,随着收发距的增大,电磁耦合增大。

图7 F s随第二层介质电阻率变化的剖面图Fig.7 Curvesof F sw ith the changesof resistivity in the second layer

3.2 层厚对电磁耦合的影响

取L、N同上,ρ1=10Ωm,ρ2=100Ωm,h1从200m到500m以100m间距逐增。从图8(见下页)看出,上层为低阻介质时,随层厚的加大,电磁耦合效应增强;反之,上层为高阻介质时,随层厚的加大,电磁耦合效应减弱。

3.3 供电极距AB变化对电磁耦合的影响

取h1=200m,ρ1=10Ωm,ρ2=100Ωm,极距AB以100m、200 m到300 m变化,取这三种供电极距测量时共同覆盖的区域。从图9可以得出结论:用偶极装置测量时,电磁耦合效应受极距AB的影响小。当ρ1>ρ2,极距AB以同样的方式变化,得到的结论相同。

图8 F s随第一层介质厚度变化的剖面图Fig.8 Curvesof F sw ith the changesof dep th in the first layer

图9 F s随极距AB变化的剖面图Fig.9 Curvesof F sw ith the changesof power-supp ly po lar distance AB

4 结论

在激电法适用的低频范围内,均匀半空间上的电磁耦合效应随频率的增大、收发距的增大,以及电阻率的降低而增大,这些规律有利于野外施工和去除电磁耦合干扰。由于层状介质上观测亦存在电磁耦合,所以对它的研究可以进一步去除这种干扰和指导野外施工。作者研究了二层介质时,中梯装置和偶极装置下多种参数变化对电磁耦合效应的影响。对于这二种装置,若电阻率变化,电磁耦合效应随任意层介质电阻率变大而减小;若层厚变化,电磁耦合效应随低阻层的相对变薄而变小。在用大收发距进行激电测量时,测量结果受电磁耦合的影响较大。另外,中梯测量时,电磁耦合在AB(供电极距)中部最强,远离中部时耦合效应会逐渐减小;且供电极距越小、离主测线越远,电磁耦合也越小。由于装置本身的特点,偶极装置下电磁耦合效应受供电极距AB的影响小。综上所述,为达到测量精度,在低阻覆盖区,不宜用过大的收发距进行激电测量。在中梯装置测量时,还应尽量避免使用大的供电极距。

[1]何继善.双频激电法[M].北京:高等教育出版社,2005.

[2]M ILLETT FB.Electrom agnetic coup lingof co llinear dipo les on a uniform half-space[J].M ining Geophysics,1967,5(2):401.

[3]SUNDE E D.Earth conduction effects in transm ission system s[M].New York:Dover,1968.

[4]W YNN J C,ZONGE K L.Electrom agnetic Coup ling,its intrinsic value,its removal and the cu ltu ral coup ling p rob lem[J].Geophysics,1972,40(5):831.

[5]DEY A,MORR ISON H F.Electrom agnetic coup ling in frequency and tim e dom ain induced po larization surveys overm u ltilayered earth[J].Geophysics,1973,38(2):380.

[6]HOHMANN GW.Electrom agnetic coup ling between groundedw ires at the surface of a two-layer earth[J].Geophysics,1973,38(5):854.

[7]ZONGE K L,W YNN JC.Recent advances and app lications in comp lex resistivity m easurem ents[J].Geophysics,1975,40(5):851.

[8]PELTON W H,WARD SH,HALLOF P G,et al.M ineral d iscrim ination and removalof inductive coup ling w ithm u ltifrequency IP[J].Geophysics,1978,43(3):588.

[9]战克,王继伦.变频法中电磁耦合的近似校正方法[J].地质与勘探,1981,17(4):40.

[10]何继善,熊彬,鲍力知,等.激发极化观测中电磁耦合的时间特性[J].地球物理学报,2008,51(3):886.

[11]熊彬,余云春.双频激电法感应耦合的数值计算与分析[J].物探化探计算技术,2009,31(1):30.

[12]KAUAH IKAUA J,ANDERSONW L.Program s EMCUPL and SCHCOPL computation of electrom agnetic coup ling on a layered halfspacew ith comp lex conductivities[C].U.S.Geo logical Su rvey Open-File Repo rt79-1430,1979:91.

P 631.3+25

A

1001—1749(2010)06—0617—04

国家自然科学基金项目(40974077)

2010-05-31

王顺国(1987-),男,甘肃永登人,硕士,主要从事电磁法数值模拟及反演成像方面的研究。