DH油田水平井储层测井解释研究
陈 伟,杨 斌,鲁洪江,昌伦杰,马 斌
(1.油气藏地质及开发工程国家重点实验室 成都理工大学,四川成都 610059;2.中国石油塔里木油田分公司 勘探开发研究院,新疆库尔勒 841000)
DH油田水平井储层测井解释研究
陈 伟1,杨 斌1,鲁洪江1,昌伦杰2,马 斌2
(1.油气藏地质及开发工程国家重点实验室 成都理工大学,四川成都 610059;2.中国石油塔里木油田分公司 勘探开发研究院,新疆库尔勒 841000)
水平井测井解释主要集中在测井仪器响应的理论模拟及各向异性的实验研究方面,远未达到实际水平井测井储层参数解释应用的深度和要求[1]。这里在对比分析DH油田水平井段与对应直井层段测井响应特征基础上,针对水平井段测井曲线进行了校正,提出使用直井取芯物性数据刻度水平井段测井曲线,来建立适应于水平井段井眼和曲线特征的孔隙度及渗透率神经网络解释模型,进而对整个研究区水平井段进行测井储层参数解释和评价。用直井储层参数对测井解释结果的检验表明,水平井测井储层参数解释精度得到了明显改善和提高,能够较好地满足三维地质建模的井属性参数精度要求。
塔里木盆地;测井解释;水平井;储层参数;神经网络
0 前言
随着石油工业的迅速发展,勘探开发的油气藏越来越复杂,水平井钻井技术作为提高单井产量和采收率的有效手段之一,在全世界范围内得到了越来越广泛的应用[12]。在未来的钻井类型中,大部份将会是水平井,因此如何获取较高精度水平井储层参数就显得尤其重要[2]。塔里木盆地DH油田东河砂岩段,可细分为十个岩性段,并钻有大量水平井,各水平井均测有感应电阻率系列、声波时差、自然伽玛曲线[3]。为了充分利用该区大量水平井测井资料,以便为东河砂岩段三维地质建模提供水平井水平段平面控制范围内的孔隙度、渗透率储层参数,作者在本文对水平井声波差、电阻率、自然伽玛等曲线进行了校正,建立了该区水平井神经网络储层参数解释模型,并获得了能够较好地满足该区东河砂岩段三维地质建模的井属性参数精度要求的水平井储层参数。
1 水平井测井响应特征
1.1 水平井较均质砂岩测井响应特征
当岩性界面远离井眼时,岩性界面不在仪器探测范围之内,测井曲线不受邻层及层界面的影响。当井段岩性较均质,各向异性较弱,并且井眼轨迹水平时,自然伽玛、电阻率和声波时差曲线变化平缓,测井曲线不受岩性界面的影响,测井曲线较可靠。
1.2 水平井角砾岩测井响应特征
研究区东河砂岩顶部,存在着一套以低自然伽玛、高电阻率、低声波时差等测井响应为特征的角砾岩层段。对比导眼井测井曲线响应特征发现:水平井顶部角砾岩测井响应与直井段的测井响应特征相似,此类井测井曲线较可靠。但部份井顶部角砾岩声波时差测井曲线出现高声波且变化大,而其导眼井对应层段的声波时差较低,因此此类井角砾岩段的声波时差值可靠性较差。
1.3 水平井岩性界面处测井响应特征
1.3.1 岩性界面自然伽玛测井响应特征
在水平井测井中,仪器一般靠近井眼下方,对下方地层较敏感。一般情况下,自然伽玛测井响应90%来自距离井壁15cm以内的地层中[4],当井眼以低角度穿过地层界面时,在自然伽玛曲线上反映出的地层界面不再是一个点,而是延滞为一个“区间”。因此在水平井中,自然伽玛曲线可以定性判断岩性的变化,确定地层界面变化区间,但难以确定准确的界面“点”。
1.3.2 岩性界面声波时差测井响应特征
声波时差测井没有方向性,研究区水平井声波时差曲线特征十分复杂,部份井可能受井眼几何形态变化的影响,声波时差曲线呈螺旋状有规律的变化。部份井地层界面与岩屑,可使声波时差出现异常跳跃,当水平井钻过地层界面时,时差曲线就会出现异常增大,这些都使得声波时差值可靠性变差。水平井地层重复时,测井曲线特征会重复出现,有时可以根据此现象来判断声波时差曲线的可信度。
1.3.3 岩性界面电阻率测井响应特征
研究区感应测井受井斜影响十分严重。对于真厚度相同的地层,随着井斜角的增大,感应测井受围岩影响越大;当井斜角较大时,感应测井曲线上出现犄角状的尖峰[4]。而当井眼在岩性界面时,犄角状尖峰将更为明显,这种尖峰使得水平井感应测井曲线出现不同程度的畸变。因此,可以根据水平井的电阻率曲线犄角状尖峰测井响应特征,来定性划分岩性界面。
2 水平井测井曲线校正
通过绘制研究区水平井各岩性段及其对应导眼井岩性段的声波时差、电阻率、自然伽玛的频率直方图,对比单井各岩性段各井测井曲线的峰值可以发现:在同井同岩性段上,水平井声波时差峰值及电阻率峰值普遍高于对应岩性段导眼井的测井曲线峰值,自然伽玛峰值与导眼井的自然伽玛峰值基本接近。基于对此差异的认识,通过统计对比方法,作者分别对水平井内的声波时差、电阻率和自然伽玛曲线进行了校正,以便于建立精度更高的水平井神经网络解释模型。
2.1 声波时差曲线校正
根据水平井各岩性段测井曲线的特征,寻找与其相对应的导眼井岩性段。对水平井声波时差曲线与导眼井声波时差曲线,进行采样并做重叠图(见图1及图2),可观察到在同一岩性段,水平井声波时差值高于导眼井对应井段内的声波时差值。
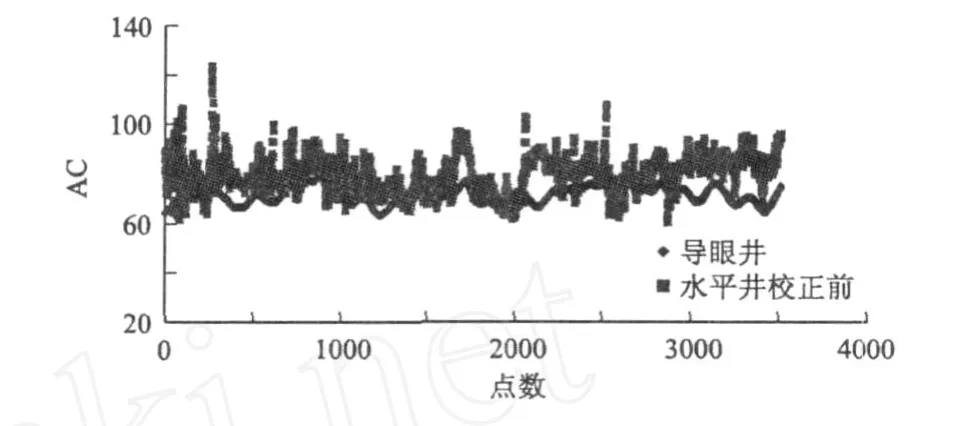
图1 X1水平井与导眼井Ⅰ岩性段声波时差曲线重叠图Fig.1 Over lapp ing im age of acoustic tim e log ofⅠlitho logic section of X1 horizontalwell vs.p ilotholewell
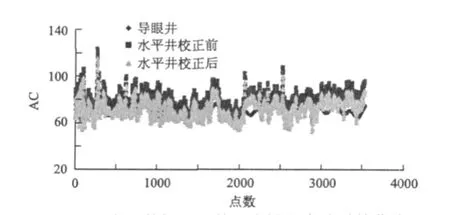
因此,对研究区水平井各岩性段声波时差曲线进行平移校正,各井各岩性段声波时差校正值由水平井与导眼井的各井各岩性段声波时差测井曲线峰值之差求得。
2.2 电阻率曲线校正
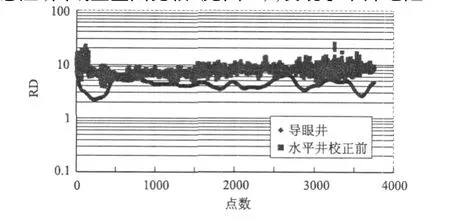
图3 X2水平井与导眼井Ⅰ岩性段深感应电阻率曲线重叠图Fig.3 Over lapp ing im age of induction resistivity log ofⅠlitho logic section of X2 horizontal well vs.p ilot ho lewell
通过相同岩性段水平井与导眼井电阻率(深感应)曲线重叠图比较(见图3),发现水平井电阻率也普遍高于导眼井的电阻率,因此,也需对研究区水平井各岩性段深感应电阻率进行平移校正。由于电阻率曲线具有非线性特征[5],所以各岩性段电阻率校正系数是由相同岩性段导眼井与水平井电阻率测井曲线峰值之比值求得。
经过校直后(见图4)的水平岩性段内,电阻率趋势值与导眼井同岩性段内的电阻率趋势值基本重合。
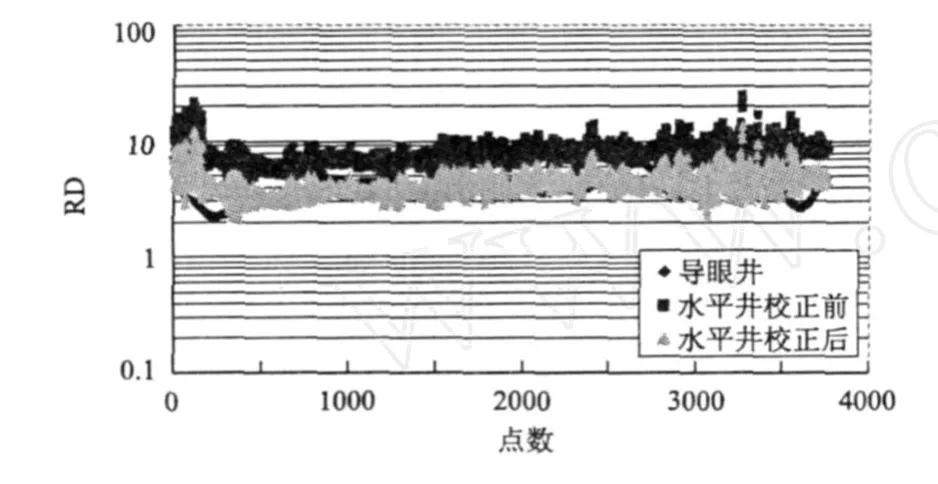
图4 X2水平井与导眼井Ⅰ岩性段深感应电阻率曲线校正前后对比曲线图Fig.4 Comparison diagram of co rrected induction resistivity log ofⅠlitho logic section of X2 ho rizontalwell vs.p ilotho lewell
2.3 自然伽玛曲线校正
自然伽玛测量仪器是径向平均测井仪器,当岩性界面不在仪器探测范围内时,自然伽玛曲线测量值不受岩性界面以及邻层的影响,能够较真实地反映出岩层的天然放射性特征。通过单井各岩性段频率直方图峰值对比,水平井自然伽玛峰值与导眼井的自然伽玛峰值基本接近。
在图5中,导眼井的自然伽玛曲线与对应岩性段水平井校直后的自然伽玛曲线趋势基本相同,因此不需要对研究区水平井自然伽玛曲线进行校正。
3 水平井储层参数解释
研究区水平井皆未取芯,因此以直井取芯物性数据刻度水平井段测井曲线[6],来建立适应于水平井段井眼和曲线特征的孔隙度和渗透率神经网络解释模型[9],进而对整个研究区水平井段进行测井储层参数的解释和评价,并用直井储层参数对水平井储层参数解释结果加以检验,获取了误差统计表。
3.1 水平井测井曲线归一化
神经网络建模要求输入曲线必须在0~1之间,因此需要对水平井测井数据进行归一化预处理。在这里,作者采用与直井相同的归一化方法,对水平井测井曲线进行归一化,各测井曲线归一化参数如表1所示。
3.2 水平井孔隙度神经网络解释模型的建立
根据研究区水平井具有的测井曲线系列,挑取八口取芯井1 265个孔隙度样本,做孔隙度与测井曲线的交会图(见下页图6)。经分析认为:岩芯分析孔隙度与自然伽玛、声波时差、深感应电阻率有一定的相关关系,因此选取自然伽玛、声波时差、深感应电阻率三条曲线作为网络输入曲线,建立孔隙度神经网络解释模型。经过网络学习、训练,当隐层单元为5时,训练误差达到最小,因此网络模型结构为3-5-1。
在学习训练完毕,岩芯分析孔隙度与网络预测孔隙度(见下页图7)相关系数R为0.89,达到了较高建模精度。
3.3 水平井渗透率神经网络解释模型的建立
水平井渗透率神经网络解释模型的建立,与孔隙度神经网络解释模型的建立类似:先挑取八口取芯井746个渗透率样本,做渗透率与测井曲线的交会图,经分析后,选取自然伽玛、声波时差、深感应电阻率、网络预测孔隙度四条曲线,作为网络的输入曲线,并建立渗透率神经网络解释模型。经过网络学习、训练,当隐层单元为8时,训练误差达到最小,因此网络模型结构为4-8-1。
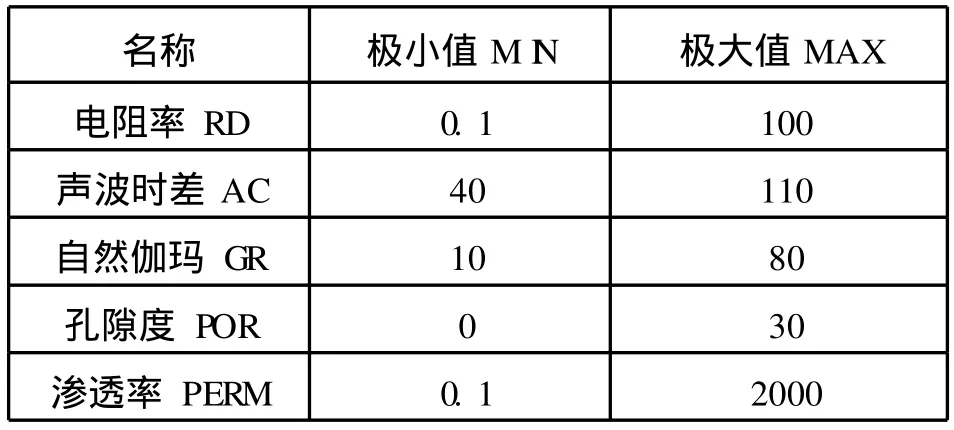
表1 DH油田水平井各测井曲线归一化参数表Tab.1 Tab le of norm alized param etersof log data of ho rizontalwell in DH oilfield
在学习训练完毕,岩芯分析渗透率与网络预测渗透率(见图8)相关系数R达到0.90。
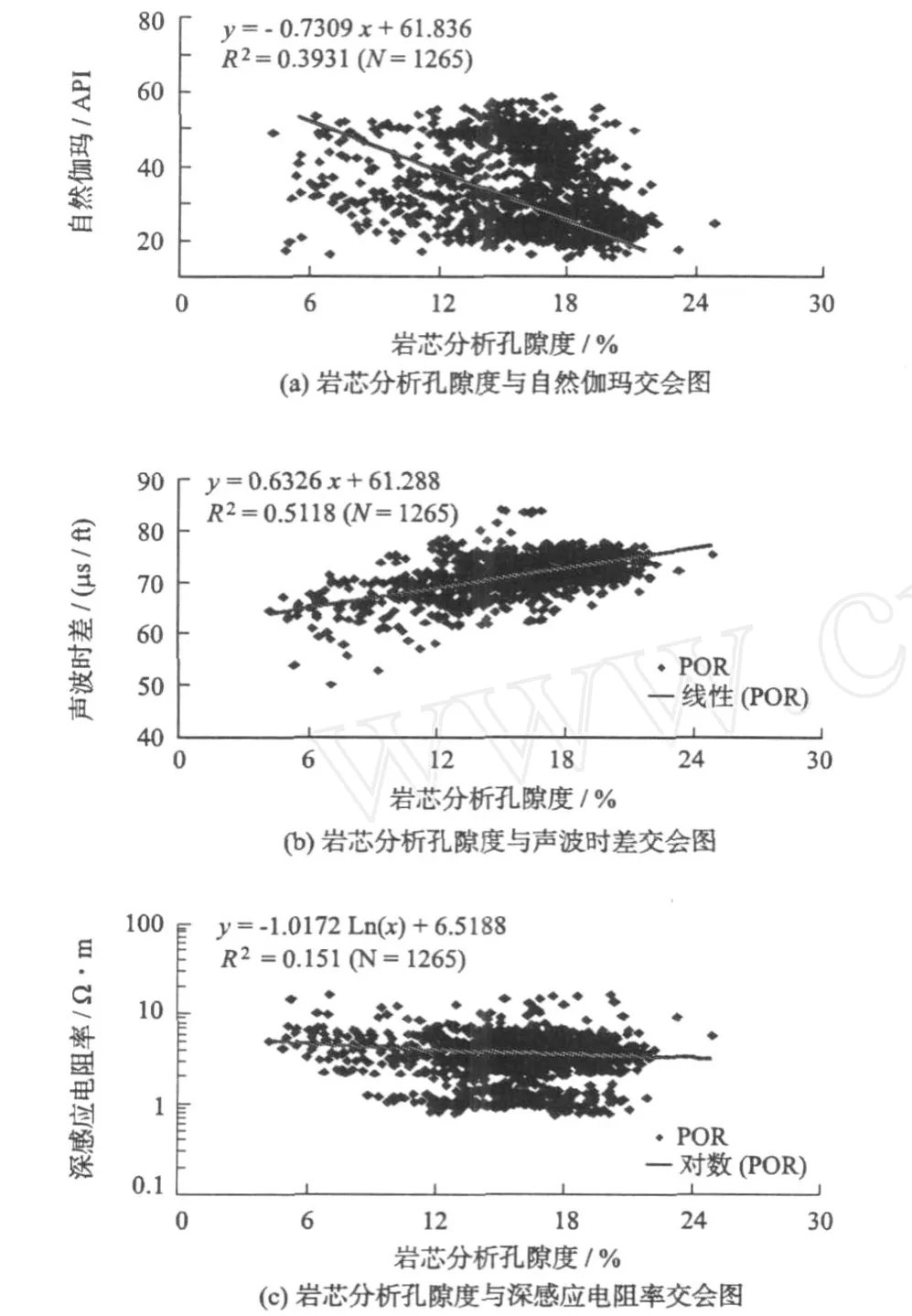
图7 岩芯分析孔隙度与网络预测孔隙度交会图Fig.7 Crossp lo tof po rosity analyzed by co re vs.po rosity p redicted by network

图8 岩芯分析渗透率与网络预测渗透率交会图Fig.8 Crossp lotof perm eability analyzed by core vs.perm eability p redicted by netwo rk
用上述建立的水平井神经网络储层参数解释模型,对研究区水平井进行储层参数处理和解释,解释精度能够较好地满足三维地质建模的井属性参数精度要求[10]。
3.4 水平井神经网络解释模型解释结果检验
由于研究区水平井均未取岩芯,所以如何检验水平井储层参数解释结果的可靠性和精度[7],还是一个十分困难的问题。作者在本文是以直井取芯物性数据刻度水平井段测井曲线,来建立适应于水平井段井眼和曲线特征的孔隙度及渗透率神经网络解释模型。因此,水平井的导眼井对应岩性段储层参数,就可以用来检验水平井储层参数解释结果。为了便于检验,首先对水平井进行水平井的井深校直[10],然后将水平井校直后的测井曲线,与直井测井曲线进行对比。
水平井在测井的过程中,大多存在深度记录上的偏差,校直后的水平井测井曲线与相对应的导眼井段,在深度上仍有较大的差异(见下页图9)。因此,要以自然伽玛曲线为基准,对水平井校直后的井深,进行垂向上、下移动。
见下页,图9(a)是X2井水平井校直后与对应导眼井的测井曲线。从图9(a)中明显看出,水平井校直后的东河砂岩段与导眼井对应的井段,在深度上存在很大的差异。自然伽玛曲线能够识别东河砂岩段,该井在水平井校直后,东河砂岩顶界面深度为5 704m,对应的导眼井深度为5 719.375m。因此,对水平井校直后的深度下移15.375m,即可得到图9(b)。在图9(b)中,X2井水平井的预测孔隙度、渗透率,与直井孔隙度、渗透率的值基本接近,变化趋势基本吻合。
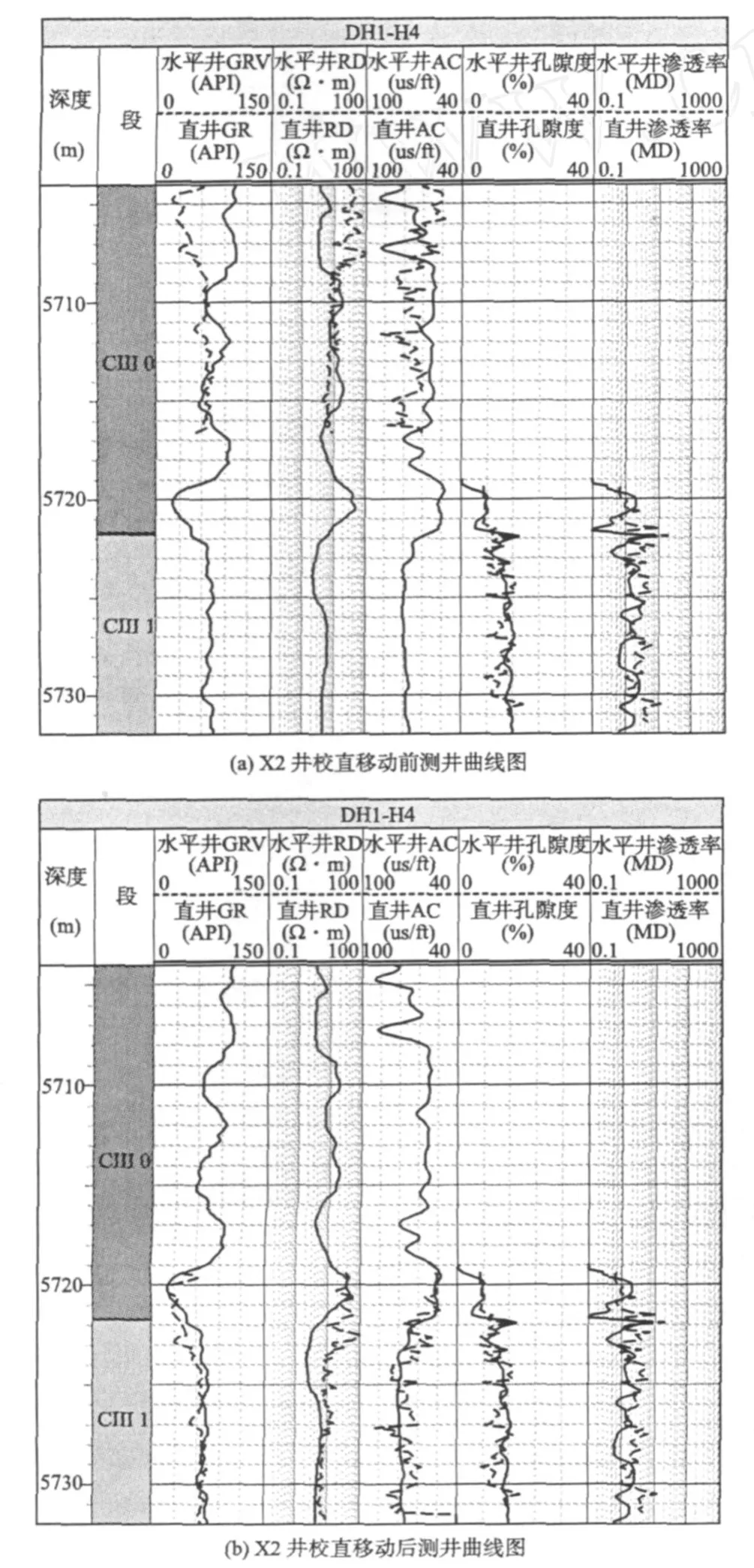
图9 X2井水平井校直移动前后测井曲线对比图Fig.9 Com parison d iagram of log before or after alignm en t of X2 horizontalw ell
图10、图11分别为X4井、X3井水平井,与导眼井储层参数测井解释成果的对比图。从图10、图11上可以看出,水平井预测孔隙度、渗透率,与直井孔隙度、渗透率吻合性较好,二者的误差(见下页表2和表3)在三维地质建模参数误差范围内,能够较好地满足三维地质建模的井属性参数精度要求。
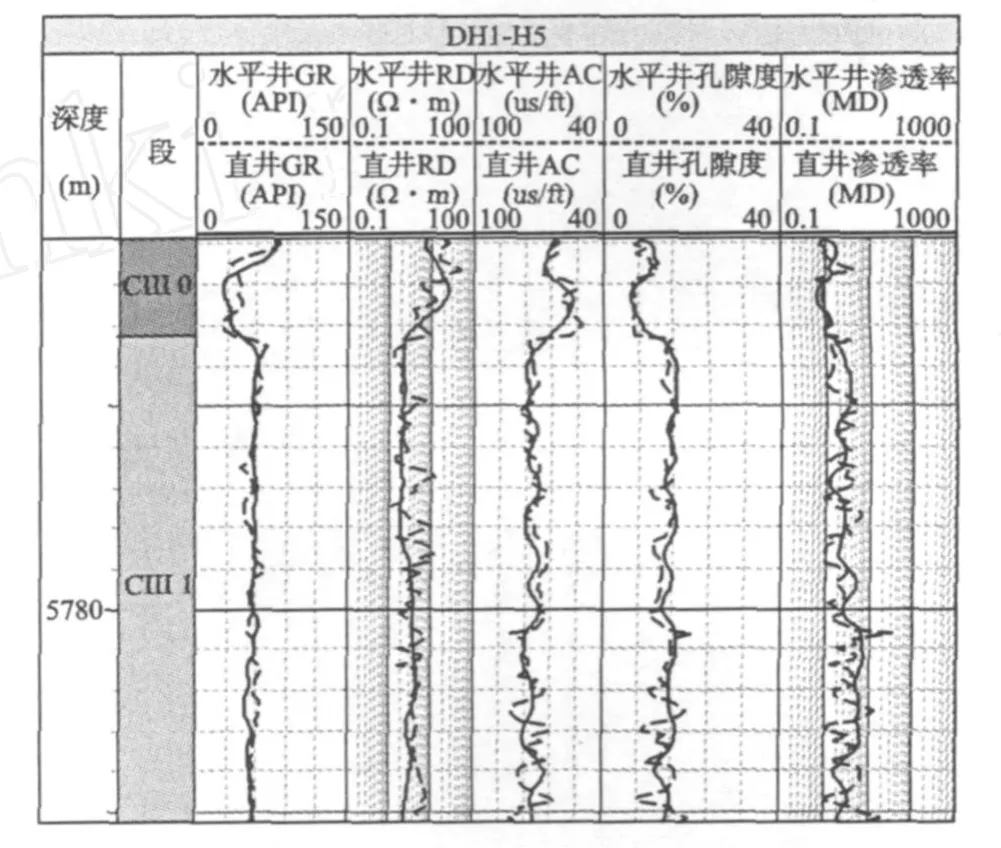
图10 X4井水平井与导眼井测井解释成果对比图Fig.10 Comparison diagram of log interp retation resultof X4 horizontalwell vs.p ilotho lewell

图11 X3井水平井与导眼井测井解释成果对比图Fig.11 Com parison diagram of log interp retation result ofX3 horizontalwell vs.p ilotho lewell
以上三口井是水平井储层参数解释效果较好的典型例子。当然,由于受研究区水平井测井曲线可靠性程度的影响,也有部份井的解释效果不佳。例如X5井水平井由于水平井段的声波时差曲线可靠性较差(见图12),使得水平井预测孔隙度、渗透率效果不佳,因此需要进一步研究其它克服这种较大差异曲线情况下,水平井储层参数解释的有效方法[8]。
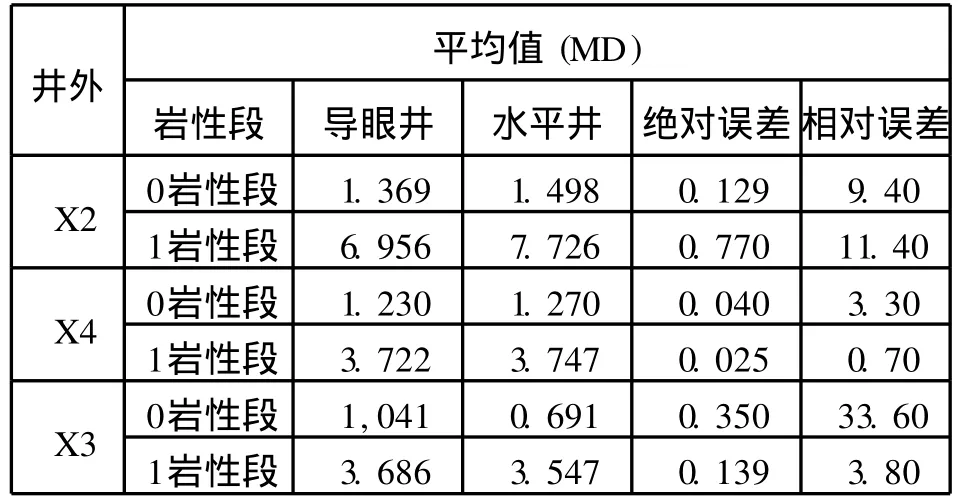
表3 水平井渗透率误差统计表Tab.3 Table of perm eability errorof ho rizontalwell
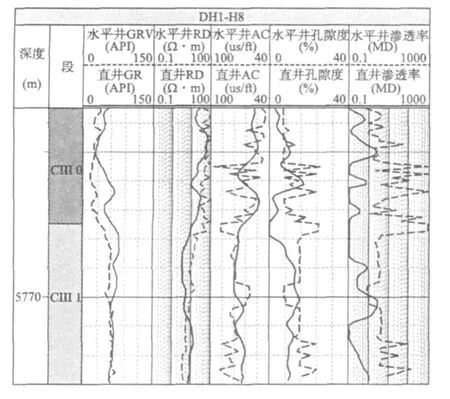
图12 X5井水平井与导眼井测井解释成果对比图Fig.12 Comparison diagram of log interp retation resu ltof X5 horizontalwell vs.p ilotho lewell
4 结论
(1)对比分析水平井段与对应直井层段测井响应特征,判断水平井测井曲线的可靠性,对水平井测井曲线进行校正是水平井储层参数神经网络解释的基础[10]。
(2)通过使用直井取芯物性数据刻度水平井段测井曲线,建立水平井储层参数解释神经网络模型经检验表明:网络模型解释的水平井储层参数,是能够较好地满足三维地质建模井属性参数精度要求。
(3)受水平井段的测井曲线(声波时差等)可靠性影响,会使得水平井储层参数解释效果不佳,因此需要进一步探索其它克服在这种较大差异曲线情况下,水平井段储层参数解释的有效方法[15]。
[1]QU INN R PASSEY,H Y IN,et al.大斜度井和水平井地层评价中的经验、问题和发展方向[J].唐宇,译.测井技术,2006,30(1):1.
[2]斯普拉克斯.水平井测井面临的挑战[A].水平井测井技术译文集[C].朱桂清,陈益鹏,杨春胜,等译.北京:石油工业出版社,1994.
[3]相建民.塔里木油田水平井高效开发技术[J].石油勘探与开发,2006,33(6):722.
[4]肖加奇,张庚骥.水平井和大斜度中的感应测井响应计算[J].地球物理学报,1995,38(3):396.
[5]汪中浩,罗少成.水平井地层电阻率各向异性研究及应用[J].石油物探,2006,45(5):546.
[6]周灿灿,王昌学.水平井测井解释技术综述[J],地球物理学进展,2006,21(1):152.
[7]刘呈冰,李厚裕.水平井测井解释原理与应用[M].东营:石油大学出版社,1993.
[8]CLAV IER C.The Challenge of Logging Horizontal W ells[J].The Log Analyst,1991,32(2):63.
[9]杨斌,匡立春.神经网络及其在石油测井中的应用[M].北京:石油工业出版社,2005.
[10]赵军,海川.水平井测井解释中井眼轨迹与油藏关系分析技术[J].测井技术,2004:45.
[11]水平井测井编写组.水平井测井技术译文集[C].北京:石油工业出版社,1995.
[12]宋文杰,朱卫红.超深超薄油藏水平井开采技术[A].中国石油学会.复杂结构井开采技术文集[C].北京:石油工业出版社,2003.
[13]陈恭洋.碎屑岩油气储层随机建模[M].北京:地质出版社,2000.
[14]吴胜河,金振奎.储层建模[M].北京:石油工业出版社,1999.
[15]CLAV IER C.The Challenge of Logging Ho rizon tal W ells[J].The Log Analyst,1991:63.
TE 122.2+3
A
1001—1749(2010)06—0645—06
2010-05-27 改回日期:2010-09-20
陈伟(1984-),男,汉族,江西吉安人,硕士,主要从事油气藏地质及储层评价研究。

