毫米波椭偏法测量介质的复介电常数

李素萍, 王子华, 张友俊, 张 胜, 李铭祥, 李 英

(1.上海大学通信与信息工程学院,上海 200072;2.上海海事大学信息工程学院,上海 200135;3.上海大学电子物理研究所,上海 201800)

毫米波椭偏法测量介质的复介电常数

李素萍1, 王子华1, 张友俊2, 张 胜1, 李铭祥3, 李 英1

(1.上海大学通信与信息工程学院,上海 200072;2.上海海事大学信息工程学院,上海 200135;3.上海大学电子物理研究所,上海 201800)

将椭圆偏振测量法(椭偏法)的电磁频谱从原来可见光、红外波段拓展到毫米波段,对毫米波椭偏法测量原理进行理论分析,使用已构建的实验装置进行测量.通过对测量结果的分析,选择合适的入射角,经过大量测试,计算出被测介质材料的复介电常数.

复介电常数;椭圆偏振测量法 (椭偏法);反射系数;毫米波

Abstract:The electromagnetic frequency band of ellip sometry is extended from visible light and infrared band to millimeter-wave band.We analyze the measurement p rinciple of ellipsometry in millimeter-wave band,and carry out experimentsusing a self-builtmeasurement apparatus.From themeasured results,an appropriate incident angle ischosen.We obtain complex permittivity of materialsbased on a large amount of measured data.

Key words:complex permittivity;ellipsometry;reflection coefficient;millimeter-wave

应用现代光电信息技术来获取物质和材料的特征信息 (如物理和结构参量)是信息科学的重要课题之一,也是信息和材料科学的交叉和结合点.电磁波的偏振是其矢量特征的标志,与波的幅度、相位、频率、时延等特性相比,具有更丰富的信息含量,故在材料特性检测中有着广泛的应用.椭圆偏振测量法(椭偏法)[1-4]是通过检测样品的反射或透射波相对入射波偏振状态的改变来准确计算出样品的光、电特性和几何参数 (如薄膜的厚度等),故与入射波的强度无关,具有高度的重复性和稳定性.椭偏法是一种高灵敏度、高精度的现代检测技术,能适应各种温度、压力和腐蚀性环境,可实现非接触、无损检测,故已广泛应用于材料 (介电材料、铁电材料、导体、半导体、超导体、合成材料、复合材料、生物材料、纳米材料等各类材料)特性等方面的测量.

可见光和红外波段的椭偏法在 20世纪 80年代已形成体系,并不断发展[5-6].微波、毫米波段的椭偏法近年来已得到各国学术界的重视[7-10],并处于探索阶段.毫米波和太赫兹波具有“似光性”,但又能穿透许多不透光的物质和材料,故构建一种新型有效的毫米波椭偏仪,并建立与之适应的测量方法,是椭偏法学科的发展前沿,不仅具有很高的学术价值,也有很广阔的应用前景.

本工作将椭偏法的电磁频谱从原来可见光、红外波段拓展到毫米波段,结合毫米波段的特点,对椭偏法的测量原理进行了分析.在毫米波段,应用本课题组已经设计完成的椭偏仪系统进行测量,计算出了被测样品的复介电常数.

1 椭偏法测量原理

当电磁波对平板样品照射时,其平行于入射面电场分量 (TM波)和垂直于入射面电场分量 (TE波)的反射系数分别为

在进行测量的过程中,电磁波斜入射样品时,正交的电磁场矢量之间会产生相位变化,即入射波相对入射面分解为平行分量和垂直分量,这两个分量经样品表面反射之后,会产生幅度和相位的变化.所以,只要得到反射波偏振状态的变化,就可求出反射后电磁波的振幅比和相位差.

为了在毫米波段测量出反射波的振幅比和相位差,本研究采用旋转角锥喇叭天线进行测量,使得接收 (检波)天线与偏振波有关,即相当于光波段椭偏法的旋转检偏器.接收天线的方位角取与入射平面相垂直的轴之间的夹角θ(当θ为 0°或 180°时,TM波的接收灵敏度最大,而 TE波的接收灵敏度最小).

毫米波椭偏法的实验测量系统,即椭偏仪装置如图1所示,主要包括信号源、隔离器、角锥喇叭天线、平方律检波器和电压表等仪器.信号源的作用是产生毫米波信号;隔离器保证了电磁波的单向传播;角锥喇叭天线用来发射和接收毫米波信号,其作用相当于光波段椭偏法中的起偏器和检偏器;接收到的毫米波信号经过放大器、检波器之后,通过电压表读出反射波的电压值.

图1 椭偏仪示意图Fig.1 Schematic draw ing of the ellipsometry apparatus

测量原理在文献[10]的基础上有所改进,本研究测量的是反射波的接收电压U和接收天线方位角θ之间的关系.

当发射天线的方位角取 +45°,即θr=+45°时,入射波以线偏振波照射到样品上,此时有等量的 TM波和 TE波入射,而观察到的反射波则为椭圆偏振波.当接收天线的方位角为θ时,接收到的反射波电压值U由下式表示:

将接收天线的方位角θi从 0°旋转到 360°,记录下所测出的 N个接收电压 U(θi)值,可求出二次傅里叶系数α,β为

当发射天线的方位角取 -45°,即θr=-45°时,反射波的接收电压U为

用角锥喇叭天线进行测量时,由于波束有一定的宽度,接收天线不能捕获到全部电波,所以当接收天线旋转时,就会产生误差.

这些由接收天线旋转所产生的高频波分量、旋转轴的错开等因素可用系数 C(θ)表示,这时测出的接收信号U可作下列修正:

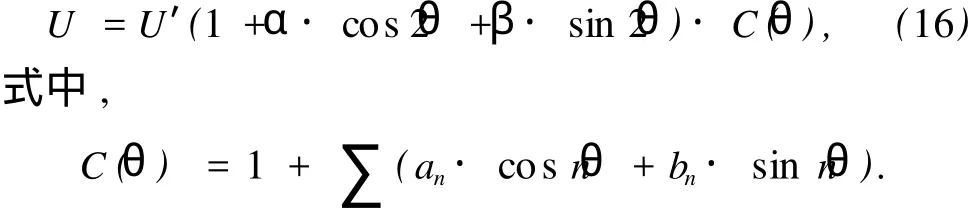
参照文献[10],用傅里叶分析校正椭偏法 (Fourier analysis correction ellipsometry,FACE)对α,β值进行修正,直至求出修正值.

因此,只要测出反射波的接收电压 U相对于接收天线方位角θ之间的关系,就可求出二次项系数α,β,然后推导出椭偏参数Ψ和Δ的值,由此可以计算出样品的复介电常数εr.

2 实验测量

2.1 入射角的选择

使用本课题组优化设计的实验装置进行实验测量.当毫米波频率 f=30.95 GHz,被测样品的厚度d=1 mm,入射角 φ =30°,55°,80°时 ,介电常数εr与椭偏参数Ψ,Δ的关系如图2所示.

图2 入射角的取值对介电常数的误差影响Fig.2 Effect of the incident angle on the com plex perm ittivity error

由图2可知,随着入射角 φ的减小,椭偏参数Ψ,Δ的曲线随介电常数εr变化的速度趋于缓慢.这说明Ψ,Δ的微小测量误差会导致介电常数εr的较大误差,也就是说,入射角越大,其对介电常数的误差影响就越小.由此可以得出如下结论:入射角的取值越大,测量结果的精度越高.

但是,当入射角过大时,收发天线之间又会产生直接耦合,从而影响到测量结果的精度.图3为入射波频率 f=30.95 GHz时,在不存在样品的情况下,接收电压 U随入射角 φ的变化关系图.由图3可知,当入射角小于 60°时,接收电压相对较小,此时可认为收发天线间不存在直接耦合.结合前面的结论,在实验测量中,选择入射角 φ=55°.

2.2 测量结果

待测样品的材料为 FR4,尺寸为 50 cm×35 cm,厚度为 0.98 mm,毫米波频率为 30.95 GHz,入射角为 55°.本课题组设计的椭偏仪装置如图4所示,使用毫米波椭偏法测量该样品的复介电常数.为了提高测量的精度,实验于微波暗室中完成.

图3 入射角与接收电压的关系图Fig.3 Relation between the incident angle and the detected voltage

图4 椭偏仪实物图Fig.4 Ellipsom etry appara tus

首先,将发射天线的方位角设为 +45°,使其对样品进行照射.接收天线的方位角从 5°旋转至360°,测量出各方位角θi所对应的电压值 Ui,测量数据如图5所示.利用式 (11)和 (12)计算得出α=-0.848 6,β=-0.517 1.

同理,将发射天线的方位角设为 -45°时,旋转接收天线,测量数据如图6所示,计算得出α=-0.847 5,β=-0.516 7.

图5 接收电压的测量值(θr=+45°)Fig.5 M easured value of the detected voltage(θr=+45°)

图6 接收电压的测量值(θr=-45°)Fig.6 M easured value of the detected voltage(θr=-45°)

计算得出α,β的平均值分别为 -0.848 1和-0.516 9.利用式 (9)和 (10)计算出椭偏参数Ψ =15.999 0°,Δ =167.285 9°.根据求出的椭偏参数采用Newton迭代法进行数据处理,得到样品的复介电常数εr=4.808 8-1.159 9i.

重复上述测量步骤,将实验数据记录在表 1中,并求出样品的复介电常数.

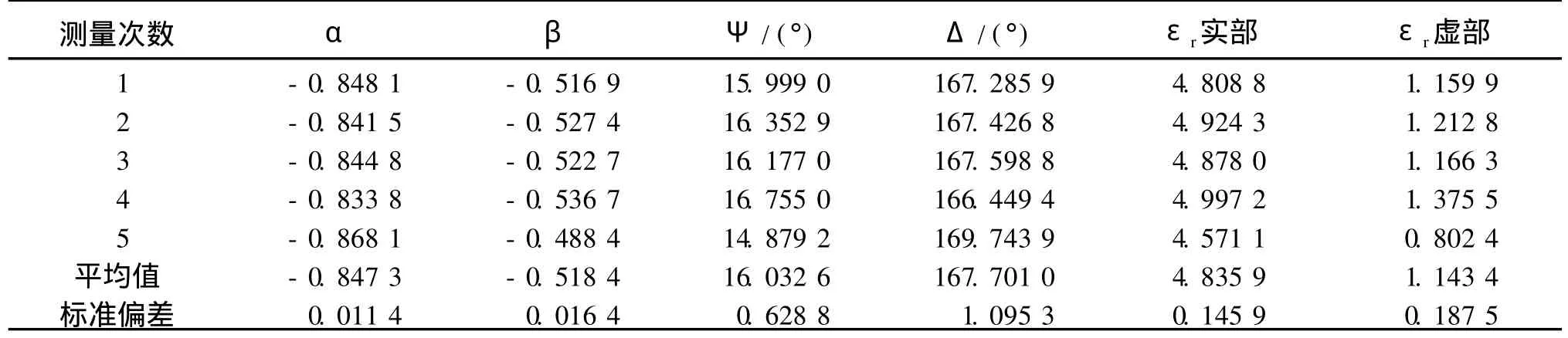
表 1 复介电常数的测量值Table 1 M easured com plex perm ittivity

由表 1可知,椭偏参数的平均值分别为Ψ =16.032 6°,Δ =167.701 0°,复介电常数的平均值为εr=4.835 9-1.143 4i,其实部和虚部的标准偏差分别为0.145 9和 0.187 5.由此可知,用毫米波椭偏法求出的复介电常数实部的测量精度比虚部高,即计算得到的虚部存在一定的误差.

在装置调试的过程中,不可避免地会存在一定的误差,这些误差包括入射角误差、信号源的频率误差、介电常数和厚度的误差、样品垂直度误差以及方位角的误差等,因此测量结果也存在一定的误差.

3 结 束 语

本工作将椭偏法的电磁频谱从原来可见光、红外波段拓展到毫米波段,对椭偏法的测量原理进行了理论分析.结合毫米波段的特点,使用已经构建的椭偏仪装置进行测量,通过对测量结果的分析,选择了合适的入射角.在毫米波段,利用椭偏法进行了大量的测量,采用 Newton迭代法进行数据处理,计算出了被测样品的复介电常数.这为毫米波椭偏法的进一步研究提供了重要的参考依据.

[1] AZZAM RM A,BASHARA N M.椭圆偏振测量术和偏振光[M].梁民基,译.北京:科学出版社,1986:12-28.

[2] SAGNARD F. Reflection ellipsometry for in-situ determination of comp lex permittivity and thickness of a single-layer material at several angles of incidence and frequencies[J].M icrowave and Optical Technology Letters,2003,36(4):243-248.

[3] 王洪涛.椭圆偏振法测量薄膜参量的数据处理 [J].物理实验,2001,21(7):8-11,17.

[4] 包学诚.椭偏仪的结构原理与发展 [J].现代科学仪器,1999(3):58-61.

[5] KAL IMANOVA I, IL IEVA N, GEORGIEVA M.Ellip sometry and thin films parameters measurement[C]∥ 28th Int Spring Seminar on Electronics Technology.2005:473-476.

[6] GUITTET P Y,MANTZ U,WEIDNER P. Infrared spectroscopic ellipsometry in semiconductor manufacturing [C]∥ IEEE/SEM I Advanced Semiconductor Manufacturing Conference. 2004:176-180.

[7] SAGNARD F,SEETHARAMDOO D,GLAUNEC V L.Reflection and transmission ellip sometry data analysis for measuring the complex permittivity of a single-layer material at microwave frequencies[J].M icrowave and Optical Technology Letters,2002,33(6):443-448.

[8] SAGNARD F.Determination of complex permittivity and thickness of a single-layer material using reflection ellipsometry at several angles of incidence [J].M icrowave and Optical Technology Letters,2002,35(2):154-157.

[9] TSUZUKIYAMA K,SAKA I T,YAMAZAKI T,et al.Ellipsometry for measurement of complex dielectric permittivity in millimeter-wave region [C]∥ 33rd European M icrowave Conference.2003:487-490.

[10] SAGNARD F,BENTABET F,V IGNAT C. In situ measurements of the comp lex permittivity of materials using reflection ellipsometry in the microwave band:experiments[J].IEEE Transactions on Instrumentation and Measurement,2005,54(3):1274-1282.

(编辑:赵 宇 )

Ellipsometry for M easurement of Complex Perm ittivity of M ater ials in M illimeter-Wave Band

L ISu-ping1, WANG Zi-hua1, ZHANG You-jun2, ZHANG Sheng1, L IM ing-xiang3, L IYing1
(1.School of Communication and Information Engineering,ShanghaiUniversity,Shanghai200072,China;2.School of Information Engineering,ShanghaiMaritime University,Shanghai200135,China;3.Institute of Electronic Physics,ShanghaiUniversity,Shanghai201800,China)

TN 015

A

1007-2861(2010)04-0371-05

10.3969/j.issn.1007-2861.2010.04.008

2009-03-09

国家自然科学基金资助项目(60571054);上海大学研究生创新基金资助项目(SHUCX080153);上海市教委支出预算资助项目(2008101)

王子华 (1946～),男,教授,博士生导师,研究方向为光纤与集成光学、光通信、微波与电磁场理论等.E-mail:zhwang@staff.shu.edu.cn