棋盘形四角锥网架屋盖动力分析

朱恩静,张亚鹏,李伍恩

(1.河北工程大学土木工程学院,河北邯郸056038;2.河北荣盛集团,河北廊坊065000)

网架常采用平面桁架系和角锥体形式,棋盘形四角锥网架是以倒置四角锥为组成单元,受压上弦杆短,受拉下弦杆长,能充分发挥杆件截面的作用,受力合理。尤其是当周边布置成满锥时,结构刚度较好,更有利于充分发挥网架结构的优越性[1]。

在地震作用下,网架结构也会受到不同程度损害。研究表明,钢结构的震害特征主要有3种破坏形式:节点连接破坏、杆件破坏和结构整体倒塌[2-3]。钢网架结构很容易因局部杆件薄弱造成杆件失稳进而整个结构倒塌。

通常对正交正放类网架、正放四角锥网架的性能掌握的较为深入,而对大跨度棋盘形四角锥网架的研究还不够完善。本文利用有限元软件SAP2000对64m～96m跨度的棋盘形四角锥网架进行模态分析和时程分析,找出其内力分布规律,为此类网架设计和施工提供理论依据。

1 网架资料

网架平面尺寸见表1,Q235钢,弹性模量E=206 Gpa,密度 ρ=7 800kg/m3,泊松比 λ=0.3。恒载标准值[4]Gk取前3级:1级为0.30 kN/m2;2级为0.85 kN/m2;3级为2.10 kN/m2。活载标准值Qk=0.50 kN/m2,上弦四周铰接支撑。

表1 网架模型尺寸Tab.1 Size of space grids m

杆件截面:(1)上弦平面,周边边弦杆采用φ 63×3.5,各边第 2、3排杆件采用 φ 133×6,其余上弦杆采用φ 152×7;(2)下弦平面,周边边弦杆采用φ 63×3.5,各边与边弦相接的杆件采用φ 114×5,其余上弦杆采用 φ 133×6;(3)腹杆,采用 φ 95×4.5。

2 模态分析

通过模态分析确定网架结构的自振周期和振型。按静力等效原则,将节点所辖区域内的荷载集中作用在该节点上[5]。采用特征向量分析法确定振型和周期,每种网架各提取前10阶振型,并获取网架结构周期。5种跨度网架的前10阶振型周期见表2。

由表2可以看出,1级荷载下,跨度每增加4m,周期约增大0.032s;2级荷载下,每增加4m,周期约增大0.042s;而在3级荷载下,跨度每增加4m,周期约增大0.057s。可以明显看出,当荷载等级一定时,周期随跨度增加而增大。

对同种跨度的网架分别在1、2、3级荷载下基本周期进行比较。软件分析时将屋面荷载转化为各节点的附加质量。附加质量越大,结构的周期越大[6-7],表2中各跨度网架均明显体现出这一规律。以64m跨度网架为例:1级荷载下周期为0.525s,2级和3级荷载下分别为0.683s、0.950s。因此可以得出,在相同跨度下,随着荷载等级增大,棋盘形四角锥网架基本周期呈增大规律。

3 ANSYS模态分析对比

利用ANSYS在同条件下建模进行模态分析,利用子空间迭代法提取模型的振型及频率,与SAP2000进行对比。现列出64m×64m、72m×72m两种跨度网架在2级、3级荷载下第一阶周期对比情况(表3)。

由表可见,SAP2000分析结果比ANSYS偏大,但相差不大,不超过10%,并且ANSYS所得周期规律与SAP2000相同,即跨度相同时,荷载等级增加,周期增大;荷载等级相同时,跨度增大,周期增大。

表2 五种跨度网架不同荷载等级下前10阶振型周期表Tab.2 Top 10 step vibration period of 5 kinds of span under different load

表3 64m、72m跨度网架基本周期表Tab.3 Vibration period of 64m and 72m span

4 网架动力分析

对5种棋盘形四角锥网架在静荷载与竖向地震组合作用下的内力分布进行了研究,图1中给出64m跨度网架在2类屋面荷载作用下的1/4部分上弦杆件静内力分布,以及Ⅱ类场地下、设防烈度为8度,场地特征周期 Tg=0.35s,竖向天津波

4.1 上弦内力分布

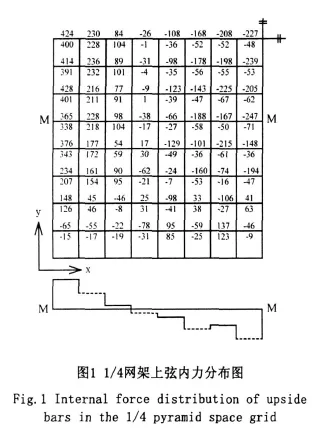
图1中杆件上侧是静内力,下侧是动内力,对比可见棋盘形四角锥网架在竖向地震作用下内力分布与静力作用时相似。对于上弦而言,不论是静力还是竖向地震作用下,轴力较大杆件的位置主要集中在网架四周靠近各边跨中央的位置,由四周的拉力向平面中心的压力过渡,隔跨呈明显递减规律。图1以M-M位置上的杆件为例,用梯形图来表示杆件内力大小,由虚实两种线型表示隔跨杆件,明显看出由四周向中部隔跨递减的规律。

4.2 下弦内力分布

对于下弦平面,因存在以对角线为轴的对称性,故取1/4下弦平面(图2),分别用①～⑦及Ⅰ～Ⅶ编号示意下弦杆件所在位置,A、B为下弦平面的两个相邻角点,OA和OB为对角线,编号1～23#示意部分下弦杆件。

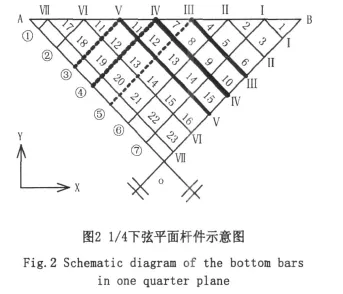
1～10#杆件在地震作用下的内力值见表4。由图2和表4得,平行于OA的杆件,越靠近OB内力越大。其中以Ⅳ-Ⅳ位置上的10#杆件内力最大(图中用线的粗细来表示杆件内力的大小,取内力最大的三个位置来示意),并向OB两端方向的杆件递减,各杆件大小依次为10#＞6#＞15#＞3#＞16#＞23#＞1#。沿OA方向也存在相似分布规律(虚线粗细表示内力大小),其中④～Ⅳ位置上靠近OA的杆件内力最大。可见内力最大值并非出现在平面中部,而是出现在1/4平面中部,并以对角线为轴对称分布。

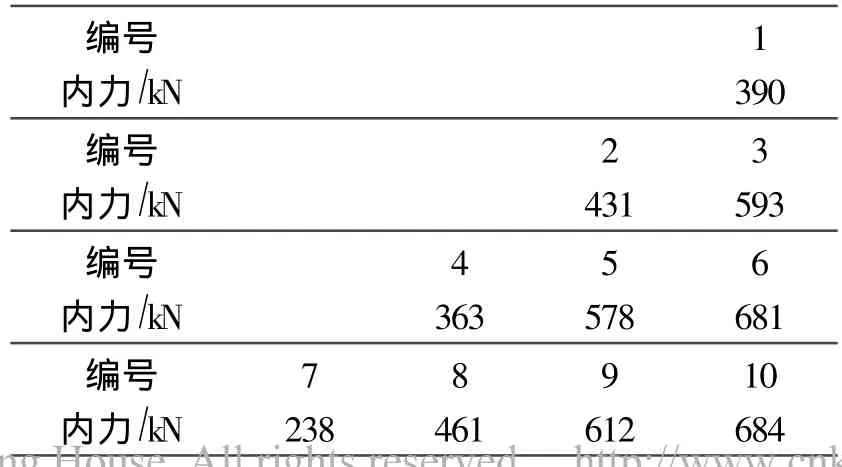
表4 1～10#下弦杆件最大动内力Tab.4 Maximum internal force of 1～10#bottom bars

4.3 腹杆内力分布

对于腹杆,拉压均存在,受力适中。取网架一角连续五跨范围内的腹杆为例(图3),横线上为杆件静内力,横线下为最大动内力。

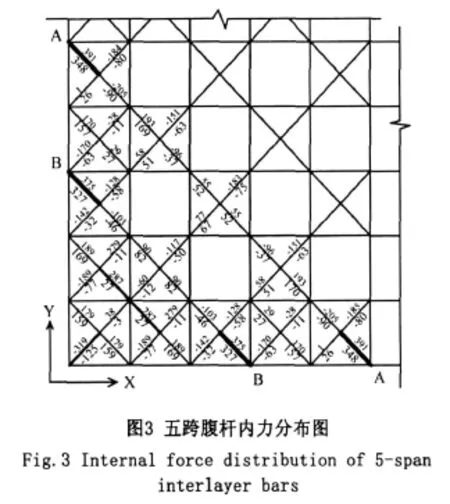
A-A和B-B位置上,两端的四角锥内腹杆内力比中间四角锥内的偏大,图中已用粗线表示内力较大杆件位置。沿轴的腹杆内力由两端向中间递减,且沿垂直轴方向的对角线对称分布。由前面下弦内力分布可知,A-A位置上杆件内力比B-B大,由此可以得出,下弦杆件内力越大,杆件所在轴两端的四角锥内腹杆内力越大。

5 结论

1)大跨度棋盘形四角锥网架基本周期受荷载等级、跨度影响,当只改变其一个因素时,周期随其增大而呈增大趋势。

2)通过对棋盘形四角锥网架的模态分析和时程分析对比,SAP2000的分析结果比ANSYS偏大,但相差不大,且都呈现相同的变化规律。

3)棋盘形四角锥网架无论是在静荷载还是在竖向地震作用下,上弦平面内力分布规律清晰,由四周的拉力向中间压力过渡,隔跨杆件呈明显递变规律;下弦内力分布则比较复杂,在1/4平面的中部为大;腹杆受下弦影响,下弦内力较大杆件所在轴两端的锥体内腹杆内力较大。

[1] 网架结构设计手册编辑委员会.网架结构设计手册(实例与图集)[M] .北京:中国建筑工业出版社,1998.

[2] 李国强,陈素文.从汶川地震灾害看钢结构在地震区的应用[J] .建筑钢结构进展,2008(4):1-8.

[3] 田黔,孟文清,赵鹏燕.焊接空心球网架节点的质量控制[J] .河北建筑科技学院学报,2003,6(2):52-54.

[4] 白那.正放四角锥网架屋盖的固有振动与竖向地震作用研究[D] .大庆:大庆石油学院,2004.

[5] 彭俊生,罗永坤,彭 地.结构动力学、抗震计算与SAP2000应用[M] .成都:西南交通大学出版社,2006.

[6] JGJ7-91.网架结构设计与施工规程[S] .

[7] 网架结构设计与施工规程编写组.网架结构设计与施工(规程应用指南)[M] .北京:中国建筑工业出版社,1995.