基于强度折减法对水电站坝头边坡稳定性分析

王庆乐,周彬

(中铁二院工程集团重庆设计研究院,重庆400015)

边坡稳定的强度折减法是通过不断降低岩土体控制性结构面强度使边坡达到极限破坏状态,从计算得到边坡的破坏滑动面和强度储备安全系数的一种计算方法。有限差分强度折减法在求解安全系数时,不需要进行条分,而是程序自动求出滑动面,同时它可以分析边坡岩体各个部位的变形状况随时间的发展演化趋势。它在边坡稳定性计算上具有很大的优越性和应用前景。本文采用有限差分强度折减法对某水电站左岸坝头开挖边坡的稳定性进行量化评价,从而为边坡工程设计和支护提供依据。

1 强度折减法原理及破坏准则

1.1 强度折减法原理

强度折减安全系数的定义与边坡稳定分析的极限平衡条分法安全系数的定义是一致的,都属于强度储备安全系数[1]。对于实际的边坡工程,它们都表示了是整个滑面的安全系数而不是某个应力点的安全系数,公式表示为

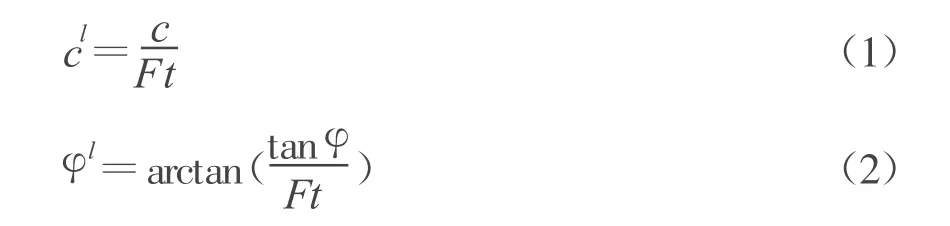
1.2 破坏准则分析

强度折减法分析边坡稳定性的一个关键问题是如何根据数值模拟的结果来判别边坡是否达到极限破坏状态。目前的失稳判据主要有4类准则[2-7]。

(1)计算不收敛。(2)结构面某一幅值的广义剪应变的贯通。(3)特征点的位移法,绘制研究对象多个特征点的位移与折减系数的关系曲线,以位移曲线出现较为明显的转折,作为达到极限破坏。(4)结构面塑性区贯通。

这4种准则在许多文献中都做过分析和比较,本人经过分析认为:准则1受数值计算软件和所建模型的质量依赖较大,作为收敛准则缺乏客观性。剪应变增量,只能确定边坡破坏的滑动方向,但不能说明是否达到破坏。由于边坡的稳定性与位移速率变化趋势将存在比较密切的关,因此准则3是比较合理的。塑性区的大范围发育和贯通,直接关系到边坡是否达到破坏,所以准则4也是较为合理的。

本文综合利用水平位移变化规律和剪应变增量的发展程度这两个判别条件共同判断边坡是否达到临界破坏状态。当水平位移增量与强度折减系数增量之比△δ/△Ft急剧变化时,并且岩土体内部形成贯通的规模较大的塑性区时,则认为边坡处于临界破坏状态,此时的强度折减系数即为边坡的安全系数[8]。

2 工程概况

某电站位于雅砻江大河湾干流河段上,大坝采用混凝土双曲拱坝方案,坝高305m。坝区河谷狭窄、谷坡陡峻、边坡高陡;自然边坡高达1 000余米,坝区整体上处于由砂板岩和大理岩构成的紧闭向斜部位,右岸为顺倾坡,左岸为反倾向坡。

坝头部位段谷坡高陡,绝大部分基岩裸露。岩性主要为砂板岩(T2-3z)和大理岩(T2-3z),另外还可见少量后期侵入的煌斑岩脉。左岸坝头自然边坡在1 850m高程以上为砂板岩边坡,坡度为40°～50°;以下为大理岩边坡,坡度为55°～70°。岩层总体产状N0°～ 30°E,NW ∠25°～45°,走向较稳定,与河流基本平行,倾向山里,属典型的逆向坡。

坝头边坡内部发育有:近EW的中等倾角小断层(如:f42-9),总体走向NNW～NNE裂隙密集带或深部裂缝,煌斑岩脉(X),f5断层,这些结构面与自然坡面共同组合,围成了一个大块体,具估算,该块体体积约340万方。按现有大坝轴线布置方案,根据左岸拱肩槽及1885以上开挖体形,坝头边坡大块体将被切割成规模不同的两个块体。一个是由f42-9、X、SL44-1、上游坡面围限的大块体(以下简称“上游大块体”);另一个是,f42-9、f5、下游坡面围限的小块体(以下简称“下游坡小块体”)。前者规模较大,根据计算,体积约250万方。后者规模较小。左岸坝头边坡的工程地质问题非常突出。这些坝头块体一旦失稳,将会对大坝带来摧毁性破坏。

3 计算模型建立

本次采用FLAC3D软件对该水电站左岸坝头边坡的开挖过程进行计算。由于地质条件的复杂性,三维建模时对地质原型进行了适当的概化。

1)计算模型所使用的坐标系,X坐标正方向与河流近平行,指向河流下游,从大坝坐标X=1 788到X=2 268,共480m;Y 轴正方向为S65°W,与河流方向近垂直,大坝坐标Y=-101.166 5到Y=598.833 5,共700m;Z坐标方向为垂向方向,正方向铅直向上,从高程Z=1 400到Z=2 250,共850m。

2)由于坝头边坡有明显的边界条件,岩层层面对坝头边坡的“大块体”影响不大,因此在数值计算中,没有考虑岩层的层面,对岩性不同的岩体只是体现在物理力学参数上。岩级考虑了3个大的岩级(Ⅱ～Ⅳ类),并将Ⅲ、Ⅳ、还细分为Ⅲ1、Ⅲ2、Ⅳ1、Ⅳ2。

3)各岩级及结构面的计算参数岩体力学参数总体上按勘测部门建议值确定。对于部分岩级的参数,根据模型中的岩级概化情况作了适当调整。左岸深拉裂缝概化为强度较低的带,选取参数时结合参考报告中的力学参数(表1)。

蓄水后地下水位的变化,可将蓄水后库水对斜坡的影响作如下考虑:浮力和坡体的软化,计算时可通过采用浮容重和软化后的力学参数来实现[9]。

表1 岩体物理力学参数表Tab.1 Main physical-mechanical parameters of rockmass

4)模型边界均采用单向约束,及顺江方向的两边界为X方向约束,横江方向的两个边界为Y向约束,底边界为Z向约束。

5)本次模拟计算,边坡岩体本构关系按按弹塑性考虑,屈服准则采用Mohr-Coulomb准则。

6)由于三维边坡地形地质条件较复杂,本文在开挖边坡表面时选择了5个监测点,其具体位置见表2。

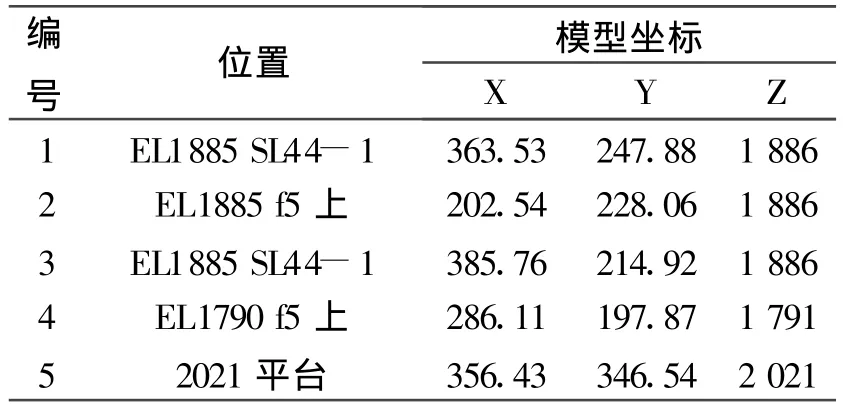
表2 监测点坐标Tab.2 Coordinate monitoring points

经过网格剖分,模型共有 48 167个节点,241 035个单元。为便于分析,沿z轴方向,在X=200m(Ⅱ-Ⅱ)、X=275m(Ⅱ1-Ⅱ1)和 X=360(V-V)处切出3个剖面。计算模型如图1所示。

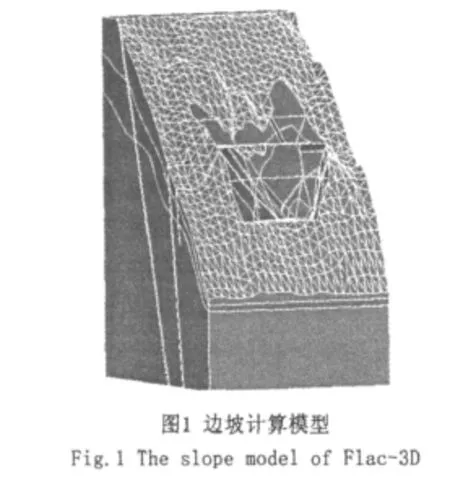
4 坝头边坡稳定性计算

4.1 蓄水前左岸坝头边坡的整体稳定性

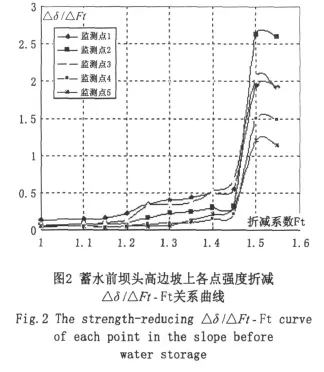
蓄水前,通过分析以上各监测点在不同强度折减系数时的水平位移,可以得到如图2所示的各节点的水平位移增量与强度折减系数增量之比值△δ/△Ft和强度折减系数Ft的关系曲线。从图2可知,在天然条件下,五个监测点的△δ/△Ft随Ft的变化趋势基本一致,当折减系数增加到1.45后,△δ/△Ft值突然急剧增加,此时岩体的塑性区范围较大,并且贯通,图3～图6典型剖面的塑性区分布图,综合△δ/△Ft-Ft的关系图和塑性区分布图,可以认为坝头开挖边坡处于临界破坏状态,此时的强度折减系数1.45即为天然条件下强度折减法计算的坝头边坡安全系数。

4.2 蓄水后左岸坝头边坡的整体稳定性

在蓄水后,通过分析各监测点在不同强度折减系数时的水平位移,可以得到如图6所示的各节点的水平位移增量与强度折减系数增量之比值△δ/△Ft和强度折减系数Ft的关系曲线。从图6可知,在天然条件下,五个监测点的△δ/△Ft随Ft的变化趋势基本一致,当折减系数增加到 1.50后,△δ/△Ft值突然急剧增加,通过图7—图9,可以看出此时岩体的塑性区较大,并且已经贯通。综合△δ/△Ft-Ft的关系图和塑性区分布图,可以认为坝头开挖边坡处于临界破坏状态,此时的强度折减系数1.50即为蓄水后天然工况下坝头边坡的安全系数。

6 结论

1)通过利用有限差分强度折减法对坝头开挖边坡的稳定性计算,可以得出,蓄水前,在天然工况下其稳定性系数为1.45;蓄水后,在天然工况下其稳定性系数为1.50。结合大块体的边界条件分析,可以认为,在施工期及蓄水工况下,左岸坝头开挖边坡蓄水前后在天然工况下,整体是稳定的。

2)对于岩质边坡而言,控制其稳定性的因素主要是发育在边坡内部的控制性结构面,应用有限差分强度折减法可以成功地解决岩体滑动面的空间组合滑动范围等问题,同时可以再现岩体各部位的变形状况随时间的发展演化趋势。

[1] 赵尚毅,郑颖人,张玉芳.极限分析有限元法讲座Ⅱ—有限元强度折减法中边坡失稳的判据探讨[J] .岩土力学,2005,26(2):332-335.

[2] 连镇营,韩国城,孔宪京,等.强度折减有限元法研究开挖边坡的稳定性[J] .岩土工程学报,2004,23(4):407-411.

[3] 栾茂田,武亚军,年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J] .防灾减灾工程学报,2003,23(3):1-8.

[4] 陈菲,邓建辉.岩坡稳定的三维强度折减法分析[J] .岩石力学与工程学报,2006,25(12):2546-2551.

[5] 李红,宫必宁,陈琰.有限元强度折减法边坡失稳判据[J] .水利与建筑工程学报,2007,5(1):79-82.

[6] 刘祚秋,周翠英,董立国,等.边坡稳定及加固分析的有限元强度折减法[J] .岩土力学,2003,24(4):644-648.

[7] 刘金龙,栾茂田.关于强度折减有限元方法中边坡失稳判据判断[J] .岩土力学,2005,26(8):1345-1348.

[8] 肖武.基于强度折减法和容重增加法的边坡稳定分析及工程研究[D] .南京:河海大学,2005.

[9] 丁秀美.西南地区复杂环境下典型堆积(填)体斜坡变形及稳定性研究[D] .成都:成都理工大学,2005.