牛顿法在隐函数中的应用

李德荣，何莉敏

（内蒙古科技大学 数理与生物工程学院，内蒙古 包头 014010）

牛顿法在隐函数中的应用

李德荣，何莉敏

（内蒙古科技大学 数理与生物工程学院，内蒙古 包头 014010）

牛顿法是求非线性方程根的一种非常重要的方法，它还可以用来求非线性方程组的根等，但是牛顿法在隐函数中的应用却鲜为人知.本文给出牛顿法在隐函数中的应用，当x给定时，如何来求对应的满足精度要求的y值.

牛顿法；隐函数；迭代

众所周知，牛顿法的应用非常广泛，它可以用来求非线性方程的单根、重根，非线性方程组的根等，但是牛顿法在隐函数中的应用却鲜为人知.下面我们就来讨论牛顿法在隐函数中的应用.

1 牛顿法简述

设xk是方程f(x)=0的一个近似根，把f(x)在xk处进行泰勒展开有：

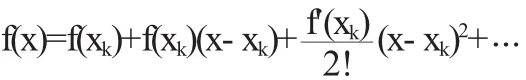
从而，将方程近似的转化为：f(xk)+f(xk)(x-xk)=0

2 隐函数定理

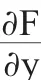
3 牛顿法在隐函数中的应用

根据上述的隐函数定理，我们知道在相当一般的条件下，方程F(x,y)=0定义了y作为x的一个函数是存在的.那么，在应用中我们经常遇到的问题是，对隐函数F(x,y)，当x给定时，如何来求y的值.如果是显函数的话，给定x，代到函数中直接可得到函数值y.当是隐函数的时候，我们就可以用牛顿法来求y的值.根据牛顿公式，将其改进为：

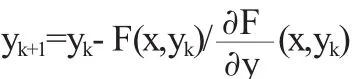
因此，当x给定时，就可得到y1,y2,…，从而，就可以得到满足精度的y值.如果，我们已经得到一对值(xn,yn)，使得F(xn,yn)=0，我们希望得到xn附近xn+1对应的值yn+1，则由(xn+1,yn)开始进行牛顿迭代.因为F(xn,yn)=0并且xn+1接近于xn，所以我们希望F(xn+1,yn)较小且很少的几步迭代就能对yn进行必要的校正，从而得到满足精度要求的yn+1的值.

例 建立一个x与y相对应的表，这里y被定义为x的一个隐函数.利用F(x,y)=3x7+2y5-x3+y3-3且从x=0开始，以0.1为步长，依次进行到x=10为止.

解 从 x=0开始，且当 x=0时，y=1.所以设 x0=0，y0=1，接下来求当x1=-.1时，y1的值.迭代从(x1,y0)开始，利用所给公式应有进行迭代，取 y=y，即：1,00(x1,y1,0)代入x1=0.1，y1,0=1依次进行4步迭代后有y1,4=1.0000077，所以求得y2=y1,4=1.0000077.利用同样的方法，可以求得x2=0.2时对应的y2的值，令y1=y2,0，迭代公式为：

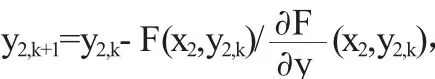
将上述算法还可以编程上机进行运算.

〔1〕David Kincaid Ward Cheney.数值分析[M]．湖北广播电视大学学报，2005：63-67.

〔2〕李有法，李晓勤.数值计算方法（第 2 版）[M].北京：高等教育出版社，2005：21-28.

〔3〕李庆扬，王能超，易大义.数值分析（第 4 版）[M].清华大学出版社，施普林格出版社，2006:276-282.

O241

A

1673-260X（2010）01-0011-01