正确理解符号函数的傅里叶变换

姜小磊

(华北电力大学(保定)计算机系,河北保定071003)

0 引言

一个符号函数sgn(t)通过连续时间傅里叶变换CTFT后可得到

不过式(1)只给出了sgn(t)的傅里叶变换在ω≠0时的取值,多数教材对此并不作解释。如果按照广义函数的观点来看待2/jω,那么有意义的不是2/jω在每个频率ω处的取值,而是2/jω对每个试验函数 (ω)的效果,即因为并不依赖于2/jω在个别点处的取值,所以讨论sgn(t)傅里叶变换在ω=0处的取值并没有意义。不过这样来理解sgn(t)的傅里叶变换会遇到一个问题:由于,所以不论试验函数 (ω)的分析性质多么良好,只要 (0)≠0,则积分就会发散。我们容易想到,这个问题可以通过取Cauchy主值来解决,即可作如下定义:

事实上,当把一个几乎在所有点处都有定义的普通函数f(ω)视作广义函数时,它对任意试验函数(ω)赋予的值并不一定是这样的形式。之所以经常用来代表f{ },是因为泛函f{ }要满足一些条件(例如线性性),而这些条件在这种特殊形式的f{ }上体现得很充分。如果不再严格按照这种形式定义f{ },那么就可以避免在原点处的奇性,从而能够解决上面的问题。

下面先叙述广义函数1/tm的定义,然后以此为基础推导出sgn(t)的傅里叶变换。需要注意的是,本文的目的是对符号函数的傅里叶变换给出一种易于为工科学生所接受的解释,所以下面的推导只是形式上的,不具有数学上的严格性。

1 广义函数t-m

为了避免在原点处的奇性[1],可以用下式来定义1/t。

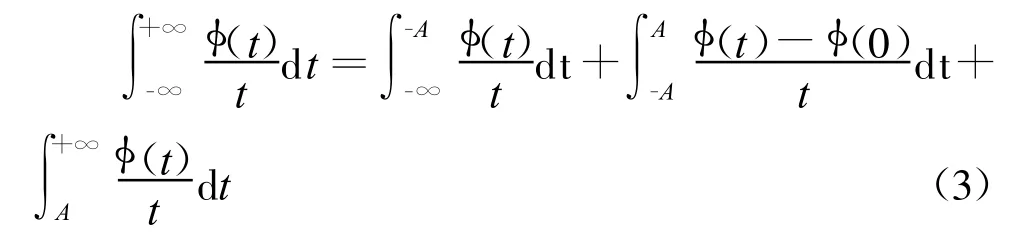
显然,式(3)的右边相对于 (t)仍然是线性的。容易看出,式(3)的右边并不依赖于A。令A※+∞可得[2]

如果令A※0+,则可得

这就是前面所述的式(2)。

1/tm(m>1)的定义可由式(3)推广得到

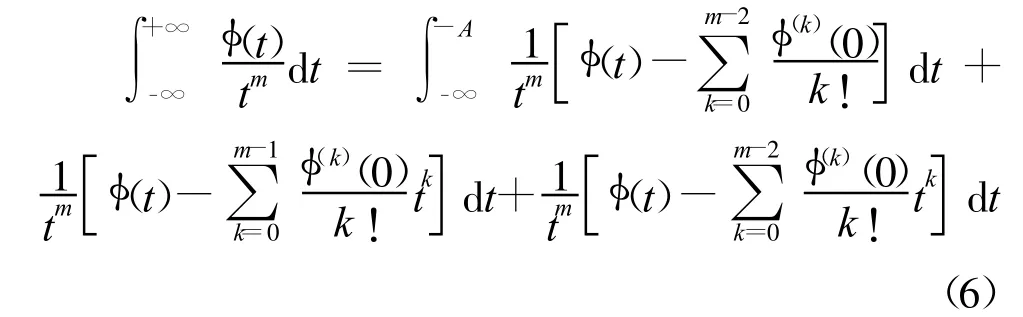
和式(3)一样,式(6)的右边相对于 (t)仍然是线性的。而且,式(6)的右边不依赖于A。令A※+∞可得

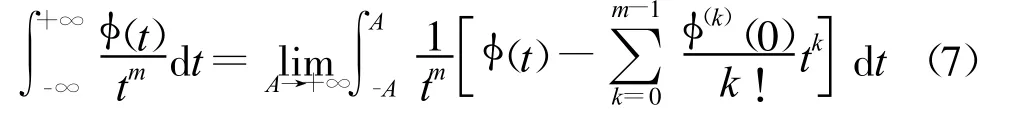
如果令A※0+,则可得

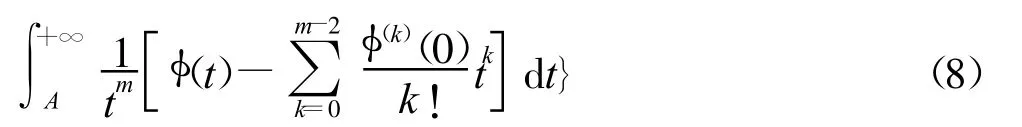
利用文献[3]的结果,可化简得到

这和冲激函数的导数的定义是一致的,即在形式上应用分部积分。

2 符号函数sgn(t)的傅里叶变换

因为下式成立:

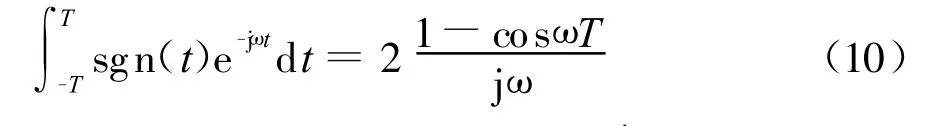
所以只需导出对任意试验函数 (ω),都有

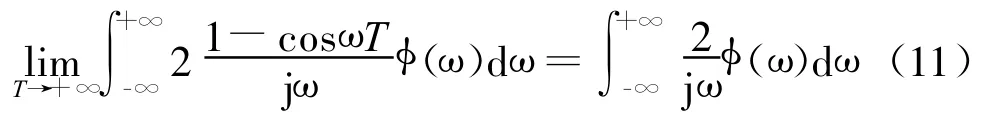
由Riemann-Lebesgue引理,式(12)右边第2项和第5项当时趋于零。下面单独考虑式(12)右边第3项:

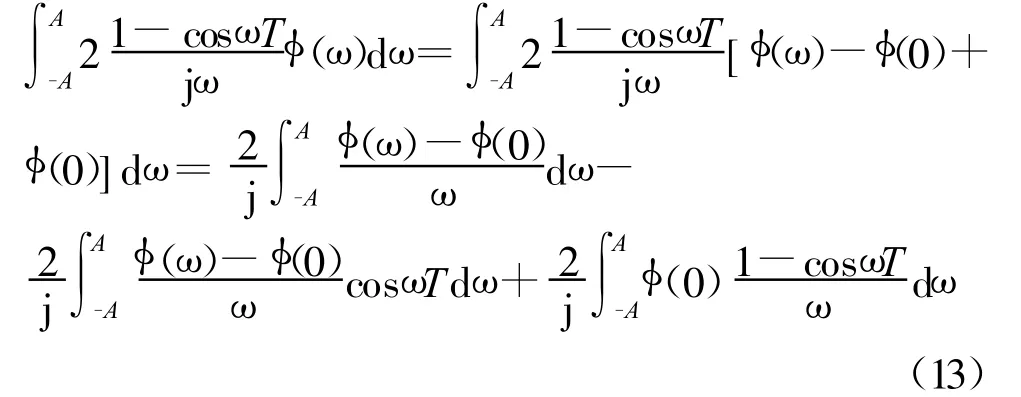
同样由Riemann-Lebesgue引理,式(13)右边第2项当时趋于零,式(13)右边第3项中的被积函数为奇函数,于是为零。综上可得

再由式(3)即得式(1)。这样sgn(t)的傅里叶变换2/jω应该按式(3)理解为广义函数(式(4)和式(5)都和式(3)等价,但有时使用起来更方便)。注意,不能直接对式(11)应用Riemann-Lebesgue引理,因为 (ω)/ω在上并非绝对可积。

3 2/jω的傅里叶反变换

我们考虑下式:

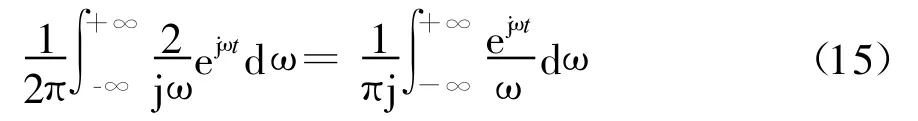
如果不把上式中的1/ω看作由式(3)所定义的广义函数,那么就会遇到积分发散的问题。由式(4)可得

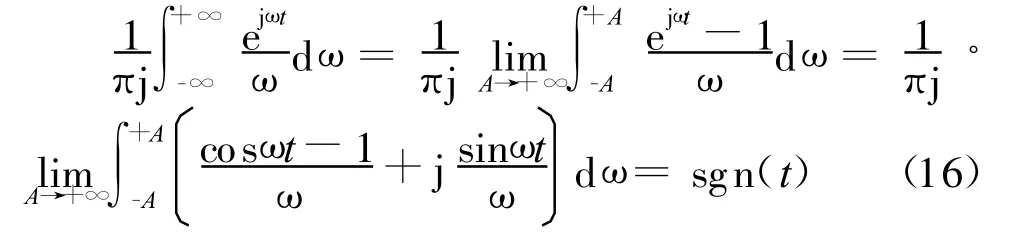
其中,利用了(cosω t-1)/ω是ω的奇函数。如果利用式(5),则同样可得

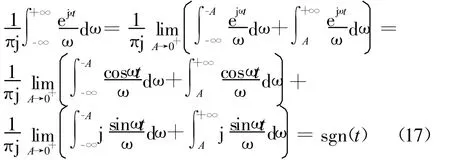
作为广义函数1/ω2的例子,下面考虑|t|的傅里叶变换,先推导正变换。

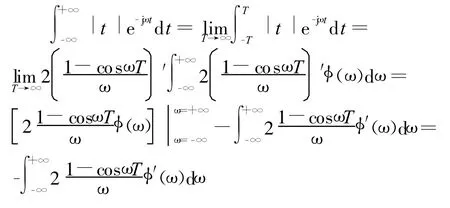
由前面已导出的式(11)即得

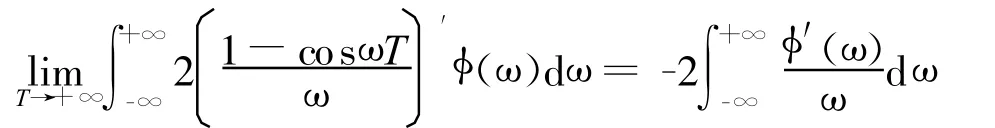
如果不把上式中1/ω2看作由式(6)所定义的广义函数,那么就会遇到积分发散的问题,即使取Cauchy主值也无法克服。类似地,对于其他涉及到负整数次幂函数的情况,例如阶跃函数的傅里叶变换也应像上面这样来理解。

4 结语

在“信号与系统”课程中,冲激函数等奇异函数是最典型的广义函数,即由其作用到其他函数上产生的效果来定义,而不是像普通函数那样由每个点处的取值来定义。与此相对应,符号函数的傅里叶变换提供了这样的例子:虽然其在几乎所有点处都有定义,但也需要在广义函数的意义下来理解。为了去除在原点的奇性,在定义这类负整数次幂函数作用到其他函数上产生的效果时需要对积分式作一点修正。明白了这些,学生在看到这类信号或者信号的傅里叶变换时就会心中有数,避免出现不应有的错误。

[1] 潘文杰.傅里叶分析及其应用[M].北京:北京大学出版社,2000

[2] David W.Kammler.A First Course in Fourier A naly sis[M].Cambridge:Cambridge University Press,2007

[3] A.Papoulis.The Fourier Integ ral and Its Applications[M].New York:McGraw-Hill,1962