矩阵的秩与运算的关系
贾美娥
(赤峰学院 数学学院,内蒙古 赤峰 024000)
矩阵的秩与运算的关系
贾美娥
(赤峰学院 数学学院,内蒙古 赤峰 024000)
矩阵的秩是线性代数中一个重要的概念,本文主要讨论矩阵运算后所得矩阵与原矩阵之间的关系.
矩阵;秩;可逆矩阵
定理1矩阵和的秩不超过两个矩阵秩的和.即秩(A+B)≤秩A+秩B
证明

A的行空间V1=L(α1,α2,…,αm)其中αi=(ai1,ai2,ai3,…,ain)i=1,2,…n
(β1,β2,β3,…βm) βi=(bi1,bi2,bi3,…bin) i=1,2,…m
B的行空间
V2=L(β1,β2,β3,…βm) βi=(bi1,bi2,bi3,…bin) i=1,2,…m
∴A+B的行空间
V3=L(α1+β1,α2+β2,…αm+βm)
∵αi+βi∈V1+V2i=1,2,…m
∴V3⊂V1+V2∴dimV3≤dim(V1+V2)
又∵dim(V1+V2)≤dimV1dimV2
∴dimV3≤dimV1+dimV2,(A+B)≤秩A+秩B
推论 两矩阵差的秩不小于两矩阵秩的差.即:秩(A-B)≥秩A-秩B
证明 A=(A-B)+B
∴秩A≤秩(A-B)+秩B
∴秩(A-B)≥秩A-秩B
定理2矩阵A与数k的乘积kA的秩当k=0时,秩(kA)=0当k≠0时,秩(kA)=秩;矩阵A与其转置矩阵A'的秩相同.
定理3矩阵乘积的秩不超过各因子的秩.即秩(AB)≤min{秩A,秩B}.
证明

B的行空间V1=L(β1,β2,β3,…βn) 其中βi=(bi1,bi2,bi3,…bis)
AB的行空间V1=L(γ1,γ2,γ3,…γm)γi=(αi1β1+αi2β2+αi3β3+…αinβn)
∵γi∈V1i=1,2,…m ∴V2⊂V1
∴dimV2≤dimV1∴秩(AB)≤秩B
同理有:秩(AB)≤秩A
∴秩(AB)≤min{秩A,秩B}
推论 数域F上m×n矩阵对于任一个m阶可逆方阵P和n阶可逆方阵
Q有秩A=秩(PA)=秩(AQ)=秩(PAQ)
证明 (1)秩(PA)≤秩A又A=P-1(PA)
∴秩A≤秩(PA) ∴秩A=秩(PA)
(2)秩(AQ)≤秩A,又A=(AQ)Q-1
∴秩A≤秩(AQ),∴秩A=秩(AQ)
由(1)和(2)得秩A=秩(PA)=秩(AQ)=秩(PAQ)
由相似矩阵和合同矩阵的定义我们又可以得出相似矩阵的秩相同,合同矩阵的秩相同.
例 证明:若A=r则A可表示为r个秩为1的矩阵的和,但不能表示为少于r个这种矩阵的和.
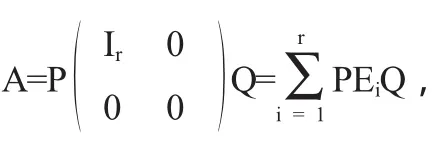
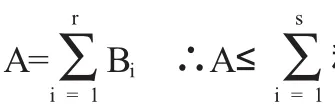

证明:秩C1≥秩C+r+s-m-n


∴秩c2≤n-s n-s是c2的列数

∴秩(C3C4)≤m-rm-r是(C3C4)的行数
∴秩C1≥秩C-C2-秩C(C3C4)≥秩C-(n-s)-(m-r)=秩C+r+s-m-n
定理4m×n矩阵A与n×s矩阵B的乘积AB的秩不小于A与B的秩的和减去n
即 秩(AB)≥秩A+秩B-n




由上面例题可知秩 秩C1≥秩c+r+p-n-c=r+p-n
又∵P1,Q2可逆
=秩C1≥r+p-n=秩A+秩B-n
推论 若两个n阶方程的乘积为零矩阵,则这两个矩阵秩的和不超过n
例 已知n阶方阵A的秩为m,求其伴随矩阵A*的秩.
解 (1)若m≤n-1则A*=0∴秩A*=0
(2)若m=n-1∴|A|=0∴AA*=0
∴秩A+秩A*≤n ∴秩A*≤1
又∵m=n-1∴A*≠0∴秩A*≥1∴秩A*=1
(3)若 m=n |A|≠0AA*=|A|I
∴|A*|=|A|n-1≠0∴秩A*=n
例 A是n阶幂等矩阵,即A2=A
求证:秩A+秩(A-I)=n.
证明 (1)秩A+秩(A-I)=秩A+秩(I-A)
≥秩(A+I-A)=秩I=n
(2) A(A-I)=A2-A=0∴秩A+秩(A-I)≤n
由(1)(2)得,秩A+(秩A-I)=n
例 已知A是n阶矩阵,A且A2=1
求证:秩(A-I)+秩(A+I)=n
证明 (1)秩(A-I)+秩(A+I)+秩(I-A)+秩(A+I)≥秩(I-A+I-A)=秩(2I)=秩I=n
(2)∵(A-I)(A+I)=A2-I=0
∴秩(A-I)+秩(A+I)≤n
由(1)、(2)得:秩(A-I)+秩(A+I)=n.
O15
A
1673-260X(2010)09-0003-02

