相移云纹干涉法对双材料界面裂纹的实验研究
李铁林
(湖南理工学院 机械工程学院,湖南 岳阳414006)
相移云纹干涉法对双材料界面裂纹的实验研究
李铁林
(湖南理工学院 机械工程学院,湖南 岳阳414006)
采用云纹干涉法和相移技术相结合对载荷作用下的正交异性双材料界面裂纹模型的位移场进行实验测定,通过计算机图像自动采集和处理,获得了实验模型的位移场云纹图.使用云纹数字图像处理软件,对实验所得位移场云纹图进行处理,可以获得界面裂纹尖端所需的实验数据,对实验数据进行处理分析,求出界面裂纹尖端的应力强度因子值.实验结果表明:在单向拉应力作用下,正交异性双材料模型的应力强度因子为复合型,且第一项对裂纹扩展起决定作用.
云纹干涉法;相移技术;双材料;界面裂纹
引言
云纹干涉法[1,2]是上世纪80年代发展起来的一种新的光测力学技术,它具有简易性、全场性、实时性、灵敏度高以及不受材料限制等优点,越来越广泛的应用于微观力学研究.相移(phase-shifting)技术[3]是提高干涉条纹测量精度的有效方法.随着计算机以及图像处理技术的发展,在云纹干涉法的基础上引进相位技术,把测量结果中的黑白条纹信息转化为相位信息,也就是把条纹本身转到条纹的相位(1/360条纹)[4],从而提高了测量精度.
本文将云纹干涉法和相移技术相结合,对正交异性双材料界面裂纹模型进行加载实验,使用CCD摄像头采集实验模型的位移云纹图.经过计算机图像处理技术,结合位移场、应变场、应力场之间的关系以及正交异性双材料界面裂纹的理论[5],可以求得界面裂纹尖端的应力强度因子值.
1 实验方法及过程
1.1 相移云纹干涉光路系统
实验采用上海711所研制的卧式结构三维云纹干涉仪,光源采用了30mw氦氖激光器.激光束通过针孔滤波后,经非球面镜变成准直光,再经过两次反射分别形成竖直平面和水平平面的二维双光束干涉光路[6].采用压电陶瓷晶体(PZT)作为相移装置,当在其上加直流电压后,压电陶瓷将会发生微小位移,带动反射镜移动;当把反射镜放在参考光路中时就会改变光程,达到改变参考光相位的目的.由于压电陶瓷晶体与加于其上的直流电压成正比关系,所以通过PZT控制器控制电压的变化就可以方便地实现相移量的连续变化.将压电陶瓷晶体相移装置引入到云纹干涉的光路中,就组成了相移云纹干涉光路,如图1所示.

图1 相移云纹干涉光路
1.2 实验过程
图1中M试件由两块同种正交异性材料板(是正交异性双材料界面裂纹的特殊情况)粘结而成,且预制边裂纹,并在试件裂纹尖端复制光栅,试件模型简图如图2所示.
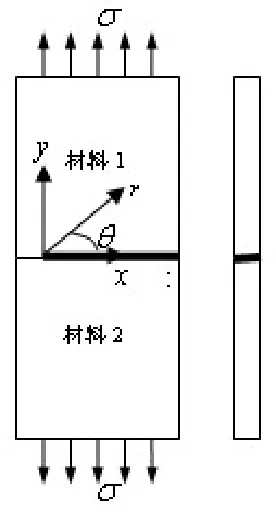
图2 试件简意图
所用材料为G3186/3266碳环氧材料,材料参数为
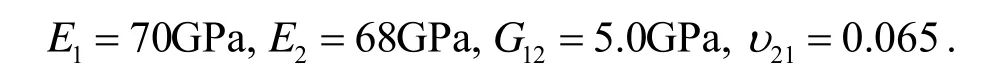
将带有光栅的试件模型置 于图1 所示的光路中,对试件进行加载,在同一载荷情况下,通过调节PZT控制电压线性变化,由CCD摄像头记录下4幅相移连续云纹图.采用相移算法,由(2)式就可以得到全场的相位分布.图3所示为载荷σ= 1.96MPa时u场位移,图3(a)是四幅记录图中的一幅位移条纹图,图3(b)是去包裹后的相位图,图3(c)为 位移场三维视图.
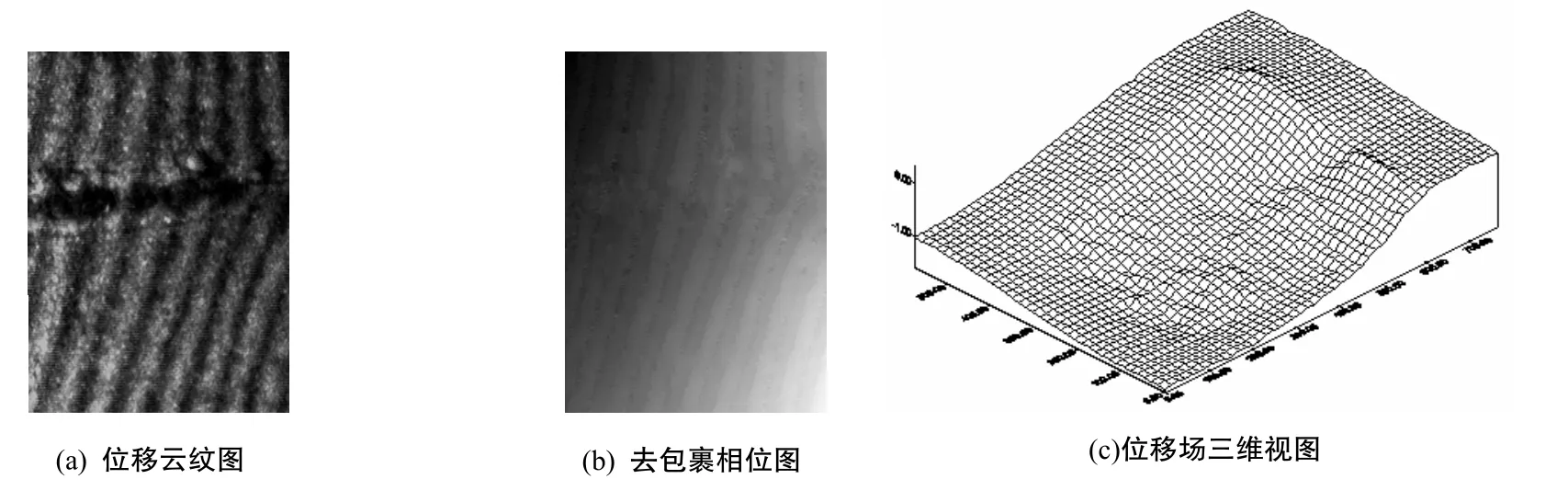
图3
2 实验结果分析
根据云纹干涉原理,由相位表示的u,v方向的位移场为

其中Φ为相位信息函数,f为云纹干涉系统中的虚栅频率,在本实验中f= 2400lines/mm.
由(1)式求出位移场后 ,代入几何方方程[7](应变场与位移场关系式),可以求得应变场,将所得应变场代入正交异性复合材料弹性主方向应力与应变场关系式[8],求出应力场.在文[8]中,推出了两种材料为同种正交异性材料时,界面上裂纹尖端应力强度因子的定义表达式为

最后将所求出的应力场代入(2)式,可以求出裂纹尖端附近区域名义应力强度因子值.在θ=0界面上,选距离裂纹尖端半径r= 0.1mm 至r=0.8mm 之间八个点求解名义应力强度因子值,各点名义 应力强度因子值见表1.

表1 裂纹尖端名义应力强度因子值
从表1中可以看 出:双材料的应力强度因子是复合型的,K1远大于K2.表中名义应力强度因子值在小范围 内波动,这是由实验误差引起的.误差有以下两个原 因:(1)试件的粘结面不够平整、粘结强度不够高;(2)试件栅衍射率比较低.由(2)式可知,在两种材料界面裂纹尖端r=0处,应力具有振荡奇异性.为了精确计算裂纹尖端附近应力场的K值,本文在范围内取值, 其中a为裂纹长度,a= 5mm.在θ=0界面上,随着 测量 点距裂纹尖端半径r的增大,K1的测量值相 应增大,K2的测量 值相应减小.通过Origin软件对表1中数据进行处理, 可以作名义应力强度因子K与的关系曲线,经回归分析,可求出r= 0时对应的应力强度因子K1和K1测试值,如图4 所示. 图中曲线1 是名义应力强度因子K1、K2与r的关系曲线,直线2是拟合曲线,由直线1、2与坐标轴的交点,可求出在r= 0处,有
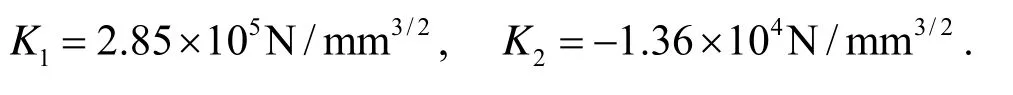

图4 名义应力强度因子K拟合曲线
3 结论
(1)相移云纹干涉法是研究双材料界面裂纹一种有效的方法,可以方便的取得在不同载荷下的位移场u,v的云纹图.
(2)通过实验可以证明:对于双材料界面裂纹,尽管只受单向拉应力作用,但尖端附近应力强度因子为复合型,即K1,K2同时存在.
(3)由实验数值可知:K1为正,K2为负,说明K1与K2方向相反,绝对值K1远大于K2,因而应力强度因子K1对裂 纹失 稳扩展起主要作用.
[1]B Han,P Ifju,D Post.Geomertric moiré methods with enhanced sensitivity by optical/digital fringe multiplication[J].Experimental Mechanics,1993,3(3):195~200
[2]潘新建,亢一澜.相移云纹干涉系统及其应用[J].力学与实践.2000,22(5):37~39
[3]D Nelson,E Fuchs,A Makino,D Willians.Residual-stress determination by single-axis holographic interferometry and hole drilling-PartⅡ,Experiments[J].Experimental Mechanics,1994,34(1):79~88
[4]孙 平,张 熹.电子散斑干涉中相移技术研究[J].光电子·激光,2001,12(11):1174~1176
[5]张少琴,杨维阳,张克颢.复合材料的Z—断裂准则及专家系统[M].北京:科学出版社,2003:12~15
[6]祝伟荣,常 红,姚河省,等.双材料界面裂纹断 裂参数 的实验测定[J].太原重型机械学院学报,2003,24(3):219~222
[7]徐芝纶.弹性力学[M].北京:高等教育出版社,2003
[8]姚河省,李铁林,张少琴.正交异性双材料界面裂纹的理论研究[J].太原科技大学学报,2006,27(2):118~1
Experimental Research of Interface Crack on Bi-materials by Phase-shifting Moiré Interferometry
LI Tie-lin
(College of Mechanical Engineering,Hunan Institute of Science and Technology,Yueyang 414006,China)
Displacement fields of orthotropic bi-material interface crack model under loading are tested by phase-shifting moiré interferometry system which is consisted by combined moiré interferometry and phase-shifting instrument.By computer image automation collecting and processing,moiré maps of displacement of the experiment model is to be gained.Then,requirement experimental data of the tip of interface crack could be obtained by using moiré digital image processing software and stress intensity factor value can be calculated with the experimental data.Experiment results show that under unilateralism tensile stress,intensity factor value of the crack tip of orthotropic bi-materials model is multiplex,and the first item plays a crucial role in crack propagation.
moiré interferometry;phase-shifting techniques;bi-material;interface crack
O348.1
A
1672-5298(2010)04-0066-03
2010-07-28
李铁林(1980− ),女,湖南宁乡人,硕士,湖南理工学院机械工程学院讲师.主要研究方向:复合材料断裂理论

