基于时态的模糊描述逻辑初探*
昌 霞,孙 瑜,冉 婕,李 静,章秀君
(云南师范大学 计算机科学与信息学院,云南 昆明650092)
在很长的一段历史时期内,逻辑学中讨论的主要是二值逻辑,随着人工智能与认知科学等的不断深入,人们认识到用二值逻辑来模拟人的思维是远远不够的。因此,非经典逻辑的产生成为必然。
时态逻辑包括命题时态逻辑和谓词时态逻辑[1],在计算机科学中应用较为广泛的命题线性时态逻辑系统PLTL,是由 PNUELI A和 MANNA Z给出的。PLTL包含可数无穷多个命题变元,以及逻辑联结词┐(否定)、∧(合 取)、∨(析 取)、⊂(蕴 含)与≡(等 价)和 时 态 算 子 □(意为“任一时刻”)、◇(意为“某一时刻”)、○(意为“下一时刻”)与>(意为“直到”)[2]。模糊逻辑从研究模糊性出发,把元素属于集合的观念模糊化,承认论域上存在着既是又非的元素;它又把属于概念量化,承认论域上的不同元素对同一集合有不同的隶属度。模糊集合论着力研究模糊推理的规律,在{0,1}中取值,恰当地处理模糊性,以适应现代科学技术的飞速发展。但模糊逻辑在表达知识的过程中并没有与时间相关联,将时态算子加入模糊描述逻辑中也是一个非常值得探讨的课题。因此,本文在模糊描述逻辑中增加适当的时态算子□、◇和○得到一种新的时态模糊描述逻辑。
1 时态逻辑基础和模糊描述逻辑
时态逻辑是关于随着时间变化而不断改变其值的动态变元(称为时序变元)的一种模态逻辑。它除含有经典逻辑的逻辑联结词和量词外,还含有一些时态算子。时态逻辑包括命题时态逻辑和谓词时态逻辑,选择不同的时态算子将导致不同的时态逻辑系统。在时态逻辑中,时间的结构可以是线性的或分支的、离散的或连续的、基于时间点的或时区的。基于不同的应用背景,可采用不同的时间结构。
针对模糊知识处理,Umberto Straccia结合模糊逻辑对传统描述逻辑ALC进行了扩充,提出了一种模糊描述逻辑FALC,从而使得描述逻辑能表示和推理模糊或不精确知识[3]。在之后的模糊描述逻辑研究中,李言辉提出了一种支持数量约束的扩展模糊描述逻辑EFALCN;Stoilos提出了比EFALCN表达能力更强的两种模糊描述逻辑f-SHIN和f-SHOIN,并且给出了f-SHOIN的ABox约束下的可满足性推理算法;蒋运承老师等人提出了一种新的面向语义Web语义表示的模糊描述逻辑FSHOIQ(fuzzy SHOIQ)[4]。
2 时态模糊描述逻辑
时态模糊描述逻辑是对模糊逻辑的扩充,模糊逻辑是针对二值逻辑表达能力不完备的一种扩展,是为解决现实世界中存在的模糊现象而发展起来的,它考虑被讨论概念属于某一类的程度,一个命题可能亦此亦彼,存在部分真和部分假。例如,张三身高1.74 m,在经典逻辑中若把1.78 m定为高个子,那么张三就不是高个子[5]。事实上,经常会这样说:“张三个子比较高”,“比较高”这样的不精确信息在二值逻辑中就无法表达。除带模糊信息之外,在现实生活中,许多的信息具有时间属性,比如说,有一个命题是“以后我将成为名人”[5],在这个命题里,“名人”具有模糊性,并且“以后”是个时间属性,所以主要来研究在已有的模糊逻辑的基础上,增加时态算子□、◇和○,构建时态模糊描述逻辑的语法、语义以及形式化公理体系。本文所研究的模糊描述逻辑是基于vague集的模糊描述逻辑,所增加的时态算子□表达的是在过去的任一时刻,◇表达的是在过去的某一时刻,比如指已过去的某一天,而○表达的是下一时刻,延伸为未来。
2.1 vague集
vague集[6]有独特的特征来处理vague数据。与普通集合相比,它具有更好的表达能力。
定义1 设U是论域,u是论域U上的元素,U上的vague集V由真隶属函数tV和假隶属函数fV来刻画。其中tV(u)是从支持u的证据中导出的u的隶属度下界;而fV(u)是从反对u的证据中得到的u的否定隶属度下界。tV(u)和 fV(u)都将区间[0,1]上的实数值与 U中的每一个元素相关联。 tV:U→[0,1],fV:U→[0,1],tV(u)+fV(u)≤1。
设 U={u1,u2,…,un}那么论域 U 上的 vague集 V 可以表示为:
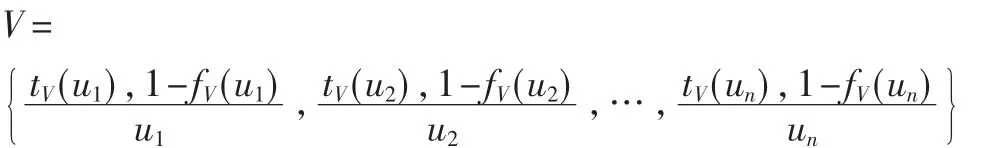
其中,tV(ui)≤μV(ui)≤1-fV(ui),∀ui∈U,1≤i≤n。
这种方法是把u的隶属度函数限定到[0,1]的子区间[tV(u),1-fV(u)]上。u的隶属函数 μV(u)的隶属值通过tV(ui)≤μV(ui)≤1-fV(ui)来限定。与u相关知识的精确差异度用1-fV(u)-tV(u)来表示。如果差异度较小,与u相关的知识就相对地更精确。如果tV(u)等于1-fV(u),与u相关的知识就是精确的,此时,vague集退化为模糊集,其中如果 tV(u)和 1-fV(u)都等于 1或 0,则vague集退化为普通集合。例如,模糊集{0.6/u}可以表示成vague集{[0.6,0.6]/u},普通集合{u}也可以用 vague 集{[1,1]/u}表示[6]。
2.2 语法
时态模糊描述逻辑的语法是模糊描述逻辑ALCN的语法的扩充。
定义2 在时态模糊描述逻辑中,概念定义为:
(1)原子概念A、全概念 ┬、和空概念⊥都是概念;
(2)如果 C和 D 是概念,则┐C、C∩D、C∪D、□C、◇C、○C都是概念;
(3)如果R为关系,C为概念,则∃R.C和∀R.C都是概念。
定义3 在T-FALC中,关系定义为:
(1)原子关系P是关系;
(2)如果R是关系,则□R、◇R、○R也是关系。
定义 4 模糊术语公理有概念包含A⊆C[4],其中A是原子概念,C是任意概念。
定义5 在时态模糊描述逻辑中,公式定义为(用<>来表达公式):
(1)形如<π[m,n]>(又写作 π⊆[m,n])的表达式,这类是不带变元的,其中 π 为 C(a)、R(a,b)、□C(a)、◇C(a)、○C(a)、□R(a,b)、◇R(a,b)或 ○R(a,b);a 和 b 是 个 体常元,□、◇和○为时态算子,0≤m≤n≤1;C为概念,R为关系,称这样的公式为断言公式;
(2)形如<π[m,n]>(又写作 π⊆[m,n])的表达式,它们是 带 变 元 的 , 其 中 π 为 C(x)、R(x,y)、 □C(x)、 ◇C(x)、○C(x)、□R(x,y)、◇R(x,y)或○R(x,y);x 和 y 是个体变元,□、◇和○为时态算子,0≤m≤n≤1;C为概念,R为关系,称这样的公式为一般公式;
(3)断言公式和一般公式都是公式;
(4)假设 ψ 和 φ 是公式,形如┐ψ、ψ∧φ、ψ∨φ、φ→ψ、∀xψ、∃yψ 都称为公式;
(5)假设φ是公式,则□φ、◇φ、○φ也是公式。
例如,<蓝色(天空)[0.6,0.8]>、<优秀学生(张三)[0.4,0.5]>、<◇天气晴朗(昆明)[0.7,0.9]>、<◇万里无云(昆明)[0.6,0.75]→◇天气晴朗(昆明)[0.6,0.75]>,这些都为T-FALC的公式。
在该系统中,时间隐含了在某个可能世界里面状态间的转换关系,一个时间片对应一个状态,对于某个概念或个体而言,它从一个状态u到另一个状态v,依赖于在状态u和v处是否分别满足公式集。例如,一块农田,现在处于轻微干旱阶段,若当前时期降雨量非常小,则该农田到下一阶段干旱现象会加重[7]。这样的一个简单状态转换可以描述为:当前状态u的公式集为{Drought(a)[0.2,0.4],Rainfall(a)[0.1,0.3]},下一状态 v 的公式集为{Drought(a)[0.5,0.7]},其中Drought是一个概念(表示对于某个具体的个体的地理状态),a代表一个个体。从状态u到状态v的推理在后面会详细说明,通过当前状态u中的公式(前提条件)推导出下一状态可能出现的概念的隶属度,来综合决策下一状态具有哪些属性(概念)。
2.3 语义
时态模糊描述逻辑的语义模型用一个三元组K=(Δ,D,I)来表示:
(1)非空集合Δ,是该系统中所讨论的所有个体对象的集合,又称为论域;
(2)非空集合D,是时态模糊描述逻辑模型中所有状态的集合,称为状态集;
(3)对该系统中的个体常元、概念和关系加以解释的映射 I。
在模糊描述逻辑中的语义是将概念解释为一定论域的模糊子集,关系是该论域上的模糊二元关系[3,8]。本文应用的是 vague 模糊解释 FI=(ΔFI,·FI),其中,解释论域ΔFI是非空的个体集合,·FI是模糊解释函数。其中解释函数·FI是将概念解释为论域 ΔFI的模糊子集,关系是该论域上的模糊二元关系。模糊解释的定义为:
定义6 对于时态模糊描述逻辑时态模糊描述逻辑中的一个状态 α,该状态下的模糊解释为 FI(α)=(ΔFI(α),·FI(α)), 其 中 ΔFI(α)是 解 释 论 域 , ·FI(α)为 解 释 函 数,并 且 解释函数·FI(α)满足以下几点:
(1)对任意 个体 a 和 b,如果 a≠b,则 aFI(α)≠bFI(α);
(2)对任意概念 C,解释函数·FI(α)将 C映射为一个隶属函数,即 CFI(α):ΔFI(α)→[α,β];
(3)对任意关系 R,解释函数·FI(α)将R映射为一个隶属函数,即 RFI(α):ΔFI(α)×ΔFI(α)→[α,β]。 其中 α∈[0,1],β∈[0,1],α 和 β分别是从 vague集的真隶属函数 tv和假隶属函数fv中得到的隶属度。在状态α下的概念C的模糊解释 CFI(α)是相对于 FI(α)的模糊概念集 C的隶属函数 , 例 如 d∈ΔFI(α)是 论 域 ΔFI(α)的 一 个 个 体 , 则 CFI(α)(d)表示在模糊解释FI(α)下个体d属于模糊概念C的程度。
定义7 时态模糊描述逻辑概念和关系的语义如下(对任意 c,d∈ΔFI(α)):
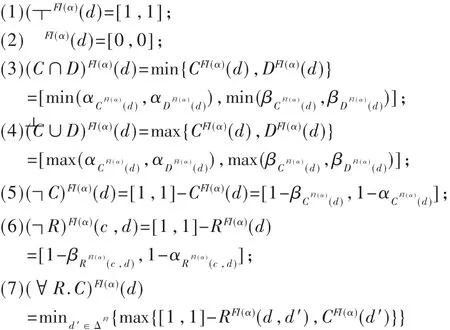

其中χ,δ代表两个不同的状态,满足在其所属世界里直接可达关系,π是指□和◇。例如,现有两个状态u和v,在 u 状态里只有一个公式{□Tall(张三)[0.7,0.9],Tall(李四)[0.6,0.7]},在 v状态里有两个公式{Tall(张三)[0.75,0.85],Height(张三)[0.4,0.7]},在通过 u状态和 v状态里,只有 Tall(张三)是相同的概念描述,就可以通过第9个算式对该概念的隶属区间加以修正。
3 一个简单的知识实例
现给出一个简单的描述某地天气状况的实例,在这里总共有 4个状态,依次定义为 t1,t2,t3,t4,再假设描述的地区对象为昆明,则通过专家系统可以获取天气在t1状态下,有公式集{fine(a)[0.5,0.8],wind(a)[0.35,0.55],overcast(a)[0.45,0.6]};t2 状 态 下 , 有 {fine(a)[0.45,0.65],wind(a)[0.3,0.5],cloud(a)[0.4,0.6]};t3 状 态 下 , 有 {wind(a)[0.35,0.65],rain(a)[0.3,0.5],cloud(a)[0.4,0.6]};t4 状 态 下 , 有 {rain(a)[0.4,0.7],overcast(a)[0.45,0.6]}。每个状态都有相应的公式集,通过相应的推理规则,可得到下一状态的概念隶属度。将所得到的概念与系统已有的同概念进行隶属区间比较,综合判定后得到下一状态会具有的属性(概念)。假设在t1状态下,通过相应的推理机制可得到 wind(a)[0.3,0.45],overcast(a)[0.1,0.3],fine(a)[0.2,0.4],则通过将这些结论与 t2状态下的公式集进行比较,可简单地对t2状态下公式进行修正,得到wind(a)[0.3,0.45]。
本文首先分析了现有描述逻辑的研究现状,特别是时态逻辑和模糊描述逻辑,针对现实生活中,有许多的信息具有时间属性并且带有模糊、不精确的特点,在时态逻辑和模糊描述逻辑基础上,提出一种新的描述逻辑,即时态模糊描述逻辑,在此基础上给出了时态模糊描述逻辑的语法和语义。进一步的工作主要是完善语法、语义及知识库的解释,并研究时态模糊描述逻辑的推理机制,包括断言公式集的一致性推理以及证明该可满足性推理算法的正确性。
[1]ZADEH L A.Outline of a new approach to the analysis of complex systems and decision processes[J].IEEE Trans.Systems,Man and Cybernetics,1973(1):28-44.
[2]玥璇.形式语义学简介[EB/OL].[2006-03-03].http://lunarxuan.bokee.com/cat.10070356.html.
[3]李龙澍,凌成.基于时态逻辑的知识表示研究[J].安徽大学学报,2002(6):14-17.
[4]蒋运承,史忠植,汤庸,等.面向语义Web语义表示的模糊描述逻辑[J].软件学报,2007(6):1257-1269.
[5]王驹,蒋运承,唐素勤.一种模糊动态描述逻辑[J].计算机科学与探索,2007(2):216-227.
[6]STRACCIA U.Reasoning within fuzzy description logics[J].Journal of Artificial Intelligence Research,2001(14):137-166.
[7]王国俊.非经典数理逻辑与近似推理[M].北京:科学出版社,2000.
[8]王星,马宗民,吕艳辉,等.Vague ALC(D):一种基于 vague集的模糊描述逻辑[J].东北大学学报,2008(11):1556-1580.

