35CrNi3MoV钢动态再结晶及高温本构关系
张景利
(中国第一重型机械集团公司,黑龙江161042)
大型锻件在高温下的变形行为复杂,涉及到加工硬化、动态恢复和动态再结晶等现象。材料产生动态再结晶,不但出现软化现象,使得应力应变关系比较复杂,而且显著影响微观组织的晶粒尺寸。研究钢材在高温下的动态再结晶规律、建立高温本构方程,可以为模拟大型锻件的热成形过程、制定锻造工艺以及控制锻件内部组织性能提供重要的基础数据[1、2]。
热压缩实验是研究钢材热成形过程中动态再结晶的主要试验手段,通过分析热压缩试验测量出的应力应变曲线建立动态再结晶的动力学模型和相应的高温本构方程[3、4]。也有研究者采用元胞自动机方法模拟计算动态再结晶过程[5]。
钢材高温变形本构方程可以归结为两类:一类是基于高温变形机理,考虑位错密度和晶粒尺寸变化与应力之间关系所提出的模型;另一类是基于实验得到的应力应变曲线,由实验数据回归得到的模型[6]。为了描述应力软化现象,考虑动态再结晶现象的本构方程多数采用分段函数形式,引入临界应变量,把变形过程分为强化回复与动态再结晶两部分。在分析位错密度变化的基础上,Laasraoui和Jonas建立了分段函数形式的本构方程[7],何宜柱等对此方程进行了推广应用,预测了ST41钢的应力应变曲线[8]。Ebrahimi等根据热压缩试验的结果,建立分段描述应力强化和应力软化曲线的数学模型,得到了Ti-IF钢热变形的本构方程[9]。
35CrNi3MoV钢是一种优质合金结构钢,具有良好的综合力学性能,常用于制造需要高强韧性的受力零件。本文研究了35CrNi3MoV钢热变形时的动态再结晶,用热压缩试验数据回归了动态再结晶参数,根据应力应变曲线的形状建立了分段式的本构方程。
1 试验方法与结果
1.1 材料成分与试验方法
试验材料为使用200 kg真空炉熔炼制得的35CrNi3MoV钢,化学成分如表1所示。将实验钢材切削加工成∅8 mm×12 mm圆柱形热压缩试样,在Gleeble 1500D热力学模拟试验机上进行热压缩试验。

表1 实验钢化学成分(质量分数,%)Table 1 The chemical composition of the test steel (mass fraction, %)
将试样以5℃/s的速度加热到变形温度,保温2 min后分别以恒定的应变速率变形,变形温度为900~1 150℃,间隔50℃;应变速率为0.05s-1,0.01s-1和0.001s-1。最大压缩变形量不低于50%,记录整个压缩过程中的应力应变曲线。在试样两端垫上0.1 mm厚的石墨片,以减小变形过程中试样与模具间的摩擦。
1.2 应力应变曲线
图1为测得的35CrNi3MoV钢高温变形应力应变曲线。当变形温度在900℃以上时,随应变增加,应力先增大后减小,这表明35CrNi3MoV钢在高温变形过程中发生了动态再结晶。变形温度越高,应力应变曲线上反映出的动态再结晶现象越明显。
表2给出了35CrNi3MoV钢动态再结晶峰值应力和峰值应变的数值。随着变形温度升高和应变速率降低,动态再结晶的峰值应力σp和峰值应变εp减小。在本文的实验条件之下,峰值应力在22.57 MPa~130.72 MPa范围内变化。

表2 35CrNi3MoV钢动态再结晶实测数据Table 2 The experimental data of dynamic recrystallization of 35CrNi3MoV steel
2 动态再结晶本构方程
2.1 动态再结晶参数的回归
采用Arrhenius方程形式的热变形方程可以建立峰值应力、稳态应力等热变形参数与应变速率和温度之间的关系。峰值应力与变形温度、应变速率的关系用Arrhenius方程表示为:
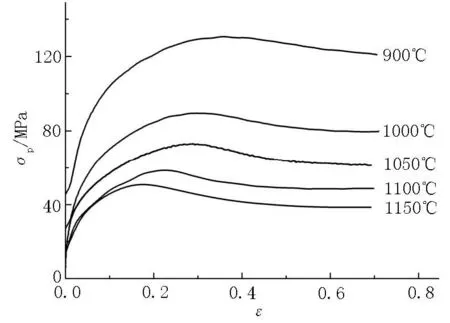



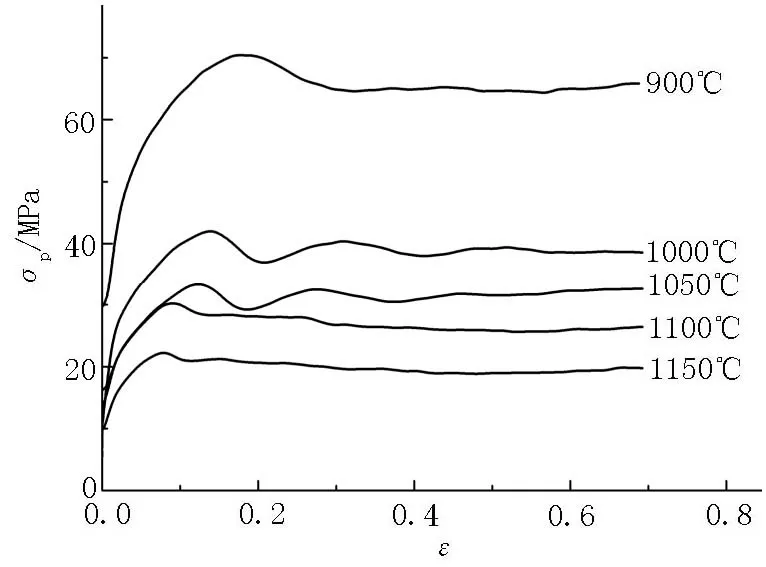
图1 35CrNi3MoV钢的高温应力应变曲线Figure 1 The stress-strain curves for 35CrNi3MoV steel at high temperatures
(1)

对公式(1)的两边取对数,整理后得到:
(2)

(3)
回归实验数据可以得到:对应峰值应力的动态再结晶激活能为313.625 kJ/mol ,常数A= 9.442 9。用相同方法,其他动态再结晶参数也可以用Arrhenius方程进行回归,但是激活能及常数A的数值不同。
2.2 分段式动态再结晶本构方程
直接对应力应变曲线的形状进行数学分析,用峰值应变作为发生应力软化的临界变量,可以建立分段式高温本构方程,预测钢在一定温度和应变速度范围内的应力应变曲线。当 时,材料热变形以加工硬化、动态回复为主,应力应变关系表示为:
σ=σp[(ε/εp)exp(1-ε/εp)]C
(4)
式中,εp是与峰值应力相对应的峰值应变,C为常数。
公式(4)中的峰值应力用热变形方程式给出:
(5)
Inεp=b+kInZ
(6)
线性回归不同温度、应变速率下的试验结果,峰值应变定义为Z参数的函数:
εp=exp(-6.384+0.199 7InZ)
(7)
对公式(4)求自然对数,可知 与函数项 成线性关系,斜率即为常数公式(4)中的常数C。在已有应力应变曲线上选取若干数据点,进行线性拟合得到:
C=0.384 8
(8)
整理上述公式,当ε<εp时,本构方程分段表达式为:
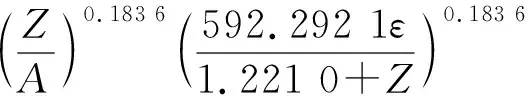
(9)
根据动态再结晶机理,发生动态再结晶后的应力软化可以用Arrhenius方程形式来描述,当ε≥εp时,本构方程分段表达式为:
式中,σstd为动态再结晶的稳态应力,常数C1是与应力软化程度相关的应力应变曲线形状特征系数。
在达到峰值应力之前的应力应变曲线上取一点εk=kεp,满足k<1、σk>σstd,可以由公式(11)得出系数C1:
(11)
式中,在公式(4)中代入εk=kεp,计算出应力σk。从试验结果来看,所选取的k值满足:0.85 与峰值应力的计算方法相同,不同温度、应变速率下的稳态应力用热变形方程式给出: (12) 回归得到:n=5.850,对应稳态应力的激活能Q=394.974kJ/mol,常数A=7567.85。 由公式(12)可以计算出某个温度和应变速率下的稳态应力数值,进而获得ε≥εp时的本构方程。 图2是用所建议本构方程计算出的应力应变曲线与实验曲线的对照。可以看出,计算值和实验值较为一致,尤其是在低应力区域。但是,在高应力区计算值与试验值存在一定的偏差。二者在高应力区有一定偏离的重要原因是:建立这个本构关系时所用到的公式(1)采用了幂函数应力关系式,幂函数应力关系式在高应力下会产生一定偏差。研究结果表明[6],采用双曲正弦应力关系式在低应力和高应力下的偏差都比较小。采用幂函数应力关系式的优点是形式简洁,易于确定本构方程中的参数,推导出来的本构方程容易应用。 在热模拟试验机上,用35CrNi3MoV钢圆柱试样进行了不同温度和变形速率下的热压缩试验。根据热压缩试验所得的应力应变曲线,用热变形方程式回归出35CrNi3MoV钢动态再结晶的峰值应力、稳态应力和峰值应变。 根据热压缩试验得到的应力应变曲线的形状,采用分段拟合的方法建立了35CrNi3MoV钢热变形的动态再结晶本构方程: 图2 35CrNi3MoV钢应力-应变曲线预测结果与实验结果的对照Figure 2 The comparison between the predicted stress-stain curves and experimental ones of 35CrNi3MoV steel σ=σstd+(σp-σstd)exp[C1(ε-0.5εp- 0.5ε2/εp)],ε≥εp 为表征应力软化现象,引入了应力应变曲线形状特征系数。用该本构方程预测出的应力应变曲线与实测的应力应变曲线符合较好,可以用所建议的本构方程计算35CrNi3MoV钢高温锻造过程。 [1] 毛卫民,赵新兵.金属的再结晶与晶粒长大.北京:冶金工业出版社,1994. [2] H. J. McQueen. Development of dynamic recrystallization theory[J]. Material Science and Engineering A, 287-389(2004): 203-208. [3] 钟云龙,刘国权,刘胜新,等. 新型油钢管33Mn2V的动态再结晶规律研究[J]. 钢铁,2003,38(2):42-46. [4] A. Yanagida, Jun Yangimoto. A novel approach to determine the kinetics of dynamic recrystallization by using the flow curve[J]. Journal of Materials Processing Technology, 151(2004): 33-38. [5] G. Kugler, R. Turk. Modeling the dynamic recrystallization under multi-stage hot deformation[J]. Acta Materialia, 52(2004): 4659-4668. [6] 周计明,齐乐华,陈国定.热成形中金属本构关系建模方法综述[J].机械科学与技术,2005(2):212-216. [7] A. Laasraoui, J. J. Jonas. Prediction of steel flow stresses at high temperatures and strain rates [J]. Metallurgical Transaction A, 1991, 22A:1545-1558. [8] 何宜柱,陈大宏,雷廷权.热变形动态软化本构模型[J].钢铁,1999,34(9):29-34. [9] R. Ebranimi, S. H. Zahiri, A. Najafizadeh. Mathematical modelling of the stress-strain curve of Ti-IF steel at high temperayure [J]. Journal of Materials Processing Technology. 2006, 171: 301-305.3 本构方程的验证
4 结论